Главная | Обратная связь

Системы параметров. Матричные параметры ЧП

Будем рассматривать проходной четырехполюсник, который можно охарактеризовать четырьмя параметрами, которые объединяются в двух уравнениях.

Всего различают 6 систем уравнений параметров.

1. Система Z-параметров – здесь напряжения выражают через токи.

Z_KN(p) – некоторые коэффициенты в уравнениях.

 

 

Исходя из данной системы уравнений, можно записать матрицу Z-параметров:

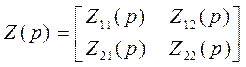
Параметры определяются, когда источник сигнала на входе.

Параметры определяются, когда источник сигнала на выходе. Z-параметры определяются в режиме холостого хода, например:

-входное сопротивление в режиме холостого хода на выходе. - передаточное сопротивление (коэф. передачи по сопротивлению) в режиме холостого хода на выходе.

Z₂₂(p) – выходное сопротивление при хх на входе.

Для обратимых ЧП выполняется равенство:

Для симметричных

2. Система Y-параметров – здесь токи выражаются через напряжения.

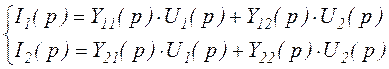
Можно записать матрицу Y-параметров:

.

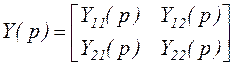Y-параметры ЧП определяются при коротком замыкании. При этом параметры определяются при коротком замыкании на выходе, а параметры 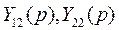- при коротком замыкании на входе. В итоге мы можем сделать вывод, что эти параметры дуальны Z-параметрам. (в обратном направлении). Для обратимых ЧП выполняется равенство: . Для симметричных

3. Система H-параметров – входное напряжение и выходной ток выражают через входной ток и выходное напряжение.

H-параметры определяются как в режиме холостого хода, так и в режиме короткого замыкания. Причем параметры определяются при коротком замыкании на выходе в прямом направлении, а параметры - при холостом ходе на входе то есть в обратном направлении.

Например,

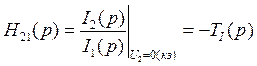. - коэффициент передачи по току в режиме короткого замыкания, но со знаком «-»..

Аналогично рассматриваются оставшиеся Н-параметры.

Для обратимых ЧП выполняется равенство: .

Для симметричных ЧП определитель системы .

 

4. Система F-параметров

F-параметры также, как и H-параметры, являются параметрами смешанного режима, т.е. параметры определяются в режиме холостого хода в прямом направлении, а параметры - в режиме короткого замыкания в обратном направлении.

Например, .

Для оценки численных результатов, необходимо учитывать, что какие-то параметры имеют размерность, а некоторые – безразмерны.

Условием обратимости ЧП является равенство: , а условием симметрии . В итоге мы можем сделать вывод, что F-параметры дуальны

Н- параметрам.

5. Система А-параметров - здесь входные величины выражают через выходные.

Иногда параметры 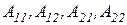обозначаются через А, В, С, D.

А-параметры определяются следующим образом:

и т.д.

Условием обратимости ЧП является: . Условием симметричности является следующее равенство: . А-параметры называют параметрами прямой передачи.

Если систему А-параметров выразить наоборот то есть выходные величины выразить через входные, то получится 6 система В-параметров (параметров обратной передачи).

Иногда используют систему входных/выходных параметров холостого хода и короткого замыкания, т.е. .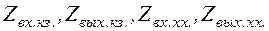

Причем, для обратимых ЧП выполняется равенство: