 |
|
С помощью второй производной
1. Найти производную 
.
2. Найти стационарные точки данной функции, т.е. точки, в которых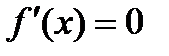 
.
3. Найти вторую производную 
.
4. Исследовать знак второй производной в каждой из стационарных точек. Если при этом вторая производнаяокажется отрицательной, то функция в такой точке имеет максимум, а если положительной, то – минимум. Если же вторая производная равна нулю, то экстремум функции надо искать с помощью первой производной.
5. Вычислить значения функции в точках экстремума.
Пример 1:Исследовать на экстремум с помощью второй производной функцию: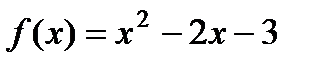 
.
Решение: Находим производную: 
.
Решая уравнение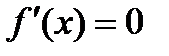 
, получим стационарную точку х =1. Найдем теперь вторую производную: 
.
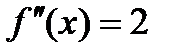Так как вторая производная в стационарной точке положительна,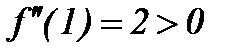 
, то при 
функция имеет минимум: 
.
Ответ: Точка минимума имеет координаты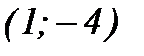 
.
Направление выпуклости графика функции.
Точки перегиба
Определение: Кривая 
называется выпуклой вниз в промежутке 
, если она лежит выше касательной в любой точке этого промежутка.
Определение: Кривая называется выпуклой вверх в промежутке , если она лежит ниже касательной в любой точке этого промежутка.
y y
x x
Определение: Промежутки, в которых график функции обращен выпуклостью вверх или вниз, называются промежутками выпуклости графика функции.
Выпуклость вниз или вверх кривой, являющейся графиком функции , характеризуется знаком ее второй производной: если в некотором промежутке 
, то кривая выпукла вниз на этом промежутке; если же 
, то кривая выпукла вверх на этом промежутке.
Определение: Точка графика функции , разделяющая промежутки выпуклости противоположных направлений этого графика, называется точкой перегиба.
y
x
Точками перегиба могут служить только критические точки II рода, т.е. точки, принадлежащие области определения функции , в которых вторая производная 
об-
ращается в нуль или терпит разрыв.