Главная | Обратная связь

Дифференциальные уравнения

 

Определение:Уравнение, связывающее независимую переменную, неизвестную функцию и ее производные или дифференциалы различных порядков, называется дифференциальным уравнением.

.

Определение:Порядком дифференциального уравнения называется порядок старшей производной, входящей в это уравнение.

(Например, y΄sinx + ytgx = 1 - первого порядка;

- второго порядка.

Определение: Функция y =φ(x), удовлетворяющая дифференциальному уравнению, называется решением этого уравнения. Решение дифференциального уравнения, содержащее столько независимых произвольных постоянных, каков порядок уравнения, называется общим решением этого уравнения.

Для уравнения 1-го порядка: y = φ(x, C)

2-го порядка: y = φ(x, C₁, C₂)

Определение: Функции, получаемые из общего решения при различных числовых значениях произвольнх постоянных, называются частными решениями этого уравнения.

Определение: Задача на нахождение частного решения дифференциального уравнения при заданных начальных условиях называется задачей Коши.

Дифференциальные уравнения с разделяющимися переменными

 

Определение: Дифференциальное уравнение с разделяющи-мися переменными имеет вид

M₁(x)·N₁(y))dx + M₂(x)·N₂(y)dy=0.

 

Алгоритм решения:

1) Поделим все члены уравнения на N₁(y)·M₂(x), получим:

, здесь переменные разделены.

2) Интегрируем обе части равенства:

,

после чего находим общее решение данного дифференциального уравнения в виде

Пример: Найти общее решение дифференциального уравнения: соs²y·ctgxdx + sin²x tgydy=0.

Решение:

Разделим на cos²y·sin²y

, переменные разделены.

Проинтегрируем обе части полученного равенства.

 

Интегралы находим методом подстановки.

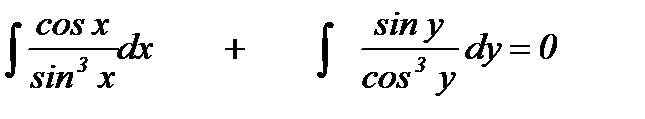
или

 

Произведя обратную подстановку, получим:

или Отсюда,

 

Ответ: - общее решение уравнения.

 

Однородные дифференциальные уравнения

Первого порядка

 

Определение:Однородной функцией переменных x и y называется функция, все члены которой имеют одинаковую степень.

Например, - однородные функции второй и третьей степени соответственно.

 

Определение: Уравнение вида , где и - однородные функции одной и той же степени, называетсяоднородным дифференциальным уравнением первого порядка.

Однородное уравнение приводится к уравнению с разделяющими переменными подстановкой, где – новая искомая функция.

Пример 1: Найти общее решение уравнения

.

Решение: Положим . Дифференцируя равенство y = ux, получим . Подставляя выражения в уравнение, получим:

Разделим переменные в полученном уравнении.

;

Интегрируем, . Отсюда, .

Сделаем обратную замену: , получим .

Ответ: .