 |
|
Свойства определителей.
Минором некоторого элемента 
определителя n-го порядка называется определитель n-1-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается 
.
Так, если 
, то 
Алгебраическим делением элемента
определителя называется его минор, взятый со знаком «плюс», если сумма i+j – четное число, и со знаком «минус», если эта сумма нечетная. Обозначается 
Так, 
.
Проиллюстрируем и одновременно докажем свойство на примере определителя 3-го порядка. В этом случае свойство означает , что 
Ы самом дела, имеем
+ 
Пример 2. Вычислите определитель матрицы
Решение: Для разложения определителя обычно выбирают тот ряд, где есть нулевые элементы, т.к. соответствующие им слагаемые в разложении будут равны нулю.
Квадратная матрица А называется невырожденной, если определитель 
не равен нулю: 
. В противном случае ( 
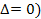матрица А называется вырожденной.
Матрица, союзной матрице А называется матрица
Где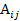 
- алгебраическое дополнение элемента 
данной матрицы А (оно определяется так же, как и алгебраическое дополнение элемента определителя).
Матрица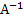 
называется обратной матрице А, если выполняется условие 
Где Е- единичная матрица того же порядка, что и матрица А. Матрица 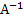имеет те же размеры, что и матрица А.
Схема нахождения обратной матрицы:
1. Выяснить вырожденная матрица А или нет.
2. Если матрица А вырожденная, то обратной матрица 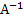не существует. Если матрица А не вырожденная, то найти союзную матрицу 
3. Найти обратную матрицу
Задания контрольной работы
Задание 1: Вычислить пределы функций:
Вариант 1:
а)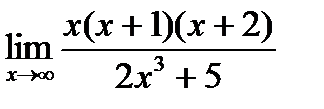 
б) 
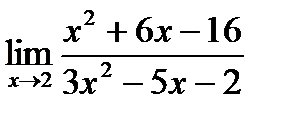в) 
Вариант 2:
а) 
б) 
в)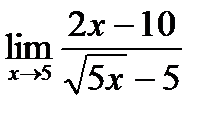 
Вариант 3:
а) 
б) 
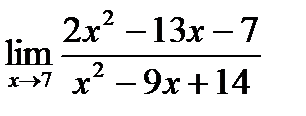в)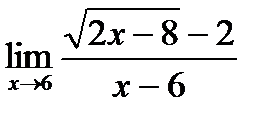 
Вариант 4:
а)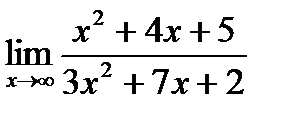 
б) 
в) 
Вариант 5:
а) 
б) 
в)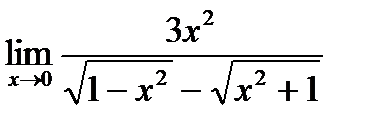 
Вариант 6:
а) 
б) 
в)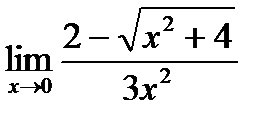 
Вариант 7:
а)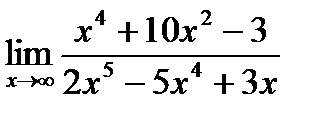 
б) 
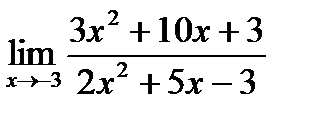в) 
Вариант 8:
а) 
б) 
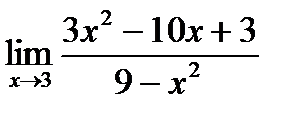в) 
Вариант 9:
а) 
б) 
в)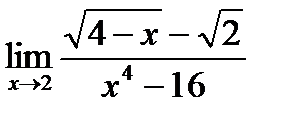 
Вариант10:
а) 
б) 
в) 