Главная | Обратная связь

Признак Даламбера сходимости строго положительного ряда

Теорема 1. Пусть строго положительный ряд. Если, начиная с некоторого номера, отношение 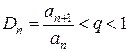, то ряд сходится, если же с некоторого номера , то ряд расходится.

Доказательство. Пусть 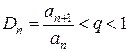при . Тогда

, , ... , , … .

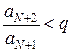Перемножая эти неравенства, получим: , откуда

. (1)

Рассмотрим ряды

, (2)

. (3)

Ряд (3) сходится как геометрическая прогрессия со знаменателем 0 < q < 1. Из неравенств (1) по признаку сравнения сходится ряд (2). Но ряд (2) есть ряд-остаток исходного ряда. Таким образом, сходится ряд .

Пусть теперь при . Отсюда при . Члены ряда не убывают, а, следовательно, общий член ряда не стремится к нулю, и ряд расходится.

На практике чаще удобнее применять предельный признак Даламбера.

Теорема 2. Пусть дан строго положительный ряд , и пусть существует конечный или бесконечный предел . Если , то ряд сходится; при ряд расходится.

Доказательство. 1) Пусть . Пусть q такое, что . Тогда найдется N такое, что при . По теореме 1 ряд сходится.

2) Пусть . Тогда и по теореме 1 ряд расходится.

Замечание. В теореме ничего не говорится о случае . В этом случае ряд может сходиться, может и расходиться. Рассмотрим ряды и 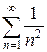. Легко показать, что для этих рядов . Первый ряд расходится, а второй сходится.

Примеры. 1) . . Ряд сходится.

2) . . Ряд расходится.

§5. Верхний и нижний пределы последовательности
действительных чисел

Пусть последовательность действительных чисел.

Определение 1. Число a называется предельной точкой последовательности , если в любой окрестности a находится бесконечно много членов .

Из определения вытекает, что если a предельная точка для , то существует подпоследовательность такая, что 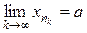. Верно, очевидно, обратное.

Теорема 1.Ограниченная последовательность имеет самую правую и самую левую предельные точки.

Доказательство. Если – ограниченная последовательность, то по известной теореме Больцано–Вейерштрасса она имеет хотя бы одну предельную точку.

Пусть E – множество предельных точек для . Множество E, как отмечено выше, не является пустым. Ясно, что E – ограниченное множество, ибо, в противном случае, последовательность была бы неограниченной. Пусть . Такое число существует по известной теореме о существовании верхней грани ограниченного числового множества действительных чисел. Если мы покажем, что , то 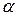и будет самой правой предельной точкой для .

Зададимся произвольным . По свойству верхней грани

.

Так как 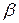предельная точка для , то при любом в окрестности будет бесконечно много членов последователь-ности .

А тогда и в ε-окрестности точки α будет бесконечно много членов .

Аналогично доказывается существование самой левой точки для E.

Замечание. Если последовательность не ограничена сверху или снизу, то множество E предельных точек может оказаться пустым, что видно из следующих примеров: 1) ; 2) .

Однако, как следует из теоремы, если множество E не является пустым, а последовательность ограничена сверху (снизу), то существует самая правая (левая) точка E.

Определение 2. Пусть дана последовательность и E – множество всех её предельных точек.

1) Если множество E ≠ Ø и последовательность ограничена сверху (снизу), то верхним (нижним) пределом называется самая правая (левая) предельная точка .

Обозначения: , .

2) Если последовательность не ограничена сверху (снизу), то полагают ( ).

3) Если множество E пустое, а последовательность ограничена сверху (снизу), то полагают ( ).

Примеры. 1) . , .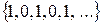

2) . , .

3) . .

4) . .

Итак, из определения следует, что всякая последовательность действительных чисел имеет верхний и нижний пределы.

Рассмотрим некоторые свойства верхнего предела последовательности:

1) Если – сходящаяся последовательность, то

.

Действительно, в этом случае имеет единственную предельную точку.

2) Если 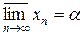, то найдётся подпоследовательность , такая, что . Верно и обратное.

Если 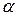– конечное число, то это было отмечено выше. Очевидно, это верно и в том случае, когда или .

Свойство верно, очевидно, и для нижнего предела.

3) Если 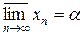, где 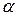– конечное, то

.

Таким образом, левее всякого числа 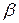, большего верхнего предела 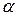, находятся все члены последовательности, начиная с некоторого номера.

Доказательство. Докажем это методом от противного. Допустим, что существует , такое, что правее находится бесконечно много членов последовательности .

Множество таких членов последовательности ограничено сверху, так как 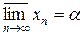– конечно число. Но тогда нашлась бы предельная точка , чего быть не может.

Аналогичные свойства можно сформулировать и для нижнего конечного предела.

4) Нам известно, что предел произведения двух сходящихся последовательностей равен произведению пределов этих последовательностей.

На верхние или нижние пределы это положение не распространяется. Покажем это на примере.

Пусть , . 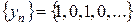, . , . Видим, что .

Рассмотрим случай, когда аналогия сохраняется.

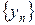Теорема 2. Пусть и – последовательности неотрицатель-ных чисел, причем , где , . Тогда

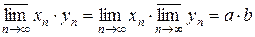
(если 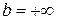, то ).

Доказательство. 1) Пусть . Точка является предельной для последовательности . Действительно, если , то найдётся такая, что . Так как , то . А тогда

.

Покажем, что – самая правая предельная точка для , то есть .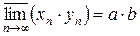

Предположим, что не есть самая правая предельная точка. Тогда найдётся предельная точка . По свойству 2) можно выделить , такую, что 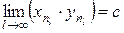, причём . Тогда

.

Заметим, что , так как . Тогда 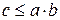, что противоречит выбору точки c.

2) Пусть 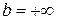. Тогда можно выделить , такую, что . Ясно, что в этом случае , так как .

§6. Признаки Коши–Адамара и Коши
сходимости положительных рядов

Теорема 1. Пусть дан положительный ряд

(1)

и . Если , то ряд сходится, если же , то ряд расходится.

Доказательство. 1) Пусть . Рассмотрим такое, что . Ясно, что 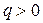. Тогда по свойству 3 верхнего предела

.

Следовательно,

при . (2)

Рассмотрим ряды 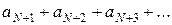и . Второй ряд сходится как геометрическая прогрессия со знаменателем . Из неравенств (2) по признаку сравнения положительных рядов сходится первый ряд, являющийся рядом-остатком ряда (1).

2) Пусть . Тогда можно утверждать, что существует подпоследовательность такая, что . Тогда

, или .

Но это означает, что общий член ряда (1) не стремится к нулю, ряд расходится.

Замечание. В теореме ничего не говорится о случае, когда . Это не случайно. При ряд (1) может, как сходиться, так и расходиться. Покажем это на примерах.

Примеры. 1) 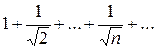; 2) 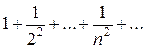. Легко проверить, что для этих рядов . При этом первый ряд расходится, а второй – сходится.

Пример.Исследовать на сходимость ряд

.

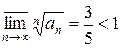. , ряд сходится.

Существуют более простые признаки типа признака Коши–Даламбера.

Теорема 2. Пусть дан положительный ряд (1). Если, начиная с некоторого номера, , то ряд сходится. Если же, начиная с некоторого номера, , то ряд расходится.

Доказательство аналогично доказательству признака Коши–Даламбера.

Теорема 3. Пусть дан положительный ряд (1) и пусть существует конечный или бесконечный предел . Если , то ряд сходится, если же , то ряд расходится.

Доказательство. Это утверждение является частным случаем теоремы Коши–Даламбера, так как в этом случае .

Следует помнить, что при ряд может сходиться, может и расходиться.

Примеры.1) .

. Ряд сходится.

2) . . 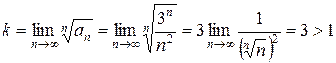Ряд расходится.