 |
|
Эквивалентность множеств
Если каждому элементу множества A сопоставлен единственный элемент множества B и при этом всякий элемент множества B оказывается сопоставленным одному и только одному элементу множества A, то говорят, что между множествами A и B существует взаимно однозначное соответствие. Множества A и B в этом случае называют эквивалентными или равномощными.
Эквивалентность множеств обозначается следующим образом: A ~ B.
Эквивалентность множеств обладает следующим свойством транзитивности.
Если A ~ B и B ~ C, то A ~ C.
Докажем это свойство. Так как A ~ B, то для всякого элемента a Î А существует единственный элемент b Î B. Но так как B ~ C, то для всякого элемента b Î B существует единственный элемент c Î C. Сопоставим этот элемент элементу a Î А. Значит, для всякого элемента a Î А существует единственный элемент c Î C и для всякого элемента c Î C существует единственный элемент a Î А. Следовательно, A ~ C.
Очевидно, что два конечных множества эквивалентны тогда и только тогда, когда количество элементов в них одинаково. Например, множества А = {4, 5, 6} и В = {x, y, z} эквивалентны, A ~ B. Взаимно однозначное соответствие может быть установлено между элементами 4 и x, 5 и y, 6 и z.
Мощностью конечного множества А (обозначается çАç) называется число элементов этого множества. Например, мощность множества А = {1, 2} равна çАç= 2.
Пример.
Ранее мы рассматривали множество всех подмножеств данного множества А, которое называется множеством-степенью и обозначается P(A). Множество P(A) состоит из 2n элементов. Таким образом, çP(A) ç = 2n.
Рассмотрим задачу определения мощности объединения n конечных множеств.
Пусть n = 2 и A и B – два пересекающихся множества. Докажем с помощью диаграммы Эйлера – Венна следующее соотношение:
çАÈB ç= çА ç+ çB ç– çАÇB ç. (1)
Из рис. 3 видим, что
çАÈB ç= n1+n2+n3;
çА ç= n1+n2;
çB ç= n2+n3;
çАÇB ç= n2.
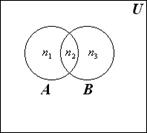
Рисунок 3.
Очевидно, что n1+n2+n3 = (n1+n2) +(n2+n3) – n2, что и доказывает формулу (1).
Формула (1) справедлива и для случая, если множества A и B не пересекаются. В этом случае
çАÈB ç= çА ç+ çB ç.
Пусть n = 3 и A, B и С – три пересекающихся множества. В этом случае справедливо следующее соотношение:
çАÈBÈ Сç= çА ç+ çB ç+ çC ç– çАÇB ç– çАÇC ç– çBÇC ç+ çАÇB ÇC ç. (2)
Из рис. 4 видим, что
çАÈBÈ Сç= n1+n2+n3+n4+n5+n6+n7;
çА ç= n1+n2+n4+n5;
çB ç= n2+n3+n5+n6;
çСç=n4+n5+n6+n7;
çАÇB ç= n2+n5;
çАÇC ç= n4+n5;
çBÇC ç= n5+n6;
çАÇB ÇC ç= n5.

Рисунок 4.
Очевидно, что
n1+n2+n3+n4+n5+n6+n7 =(n1+n2+n4+n5) + (n2+n3+n5+n6) +(n4+n5+n6+n7) – (n2+n5) – (n4+n5) – (n5+n6) + n5,
что и доказывает формулу (2).
Формула (2) справедлива и для случая, если множества A, B и С попарно не пересекаются. В этом случае
çАÈBÈ Сç= çА ç+ çB ç+ çC ç.
В общем случае мощность объединения n множеств определяется по формуле:
çА1È А2 È…ÈАnç= çА1ç+çА2ç+…+ çАnç– (çА1Ç А2ç+ çА1Ç А3ç+ … +çАn–1ÇАnç)+ çАÇB ÇC ç+ (çА1Ç А2 Ç А3ç + … +çАn–2ÇАn–1ÇАnç) – … + (–1)n – 1 çА1ÇА2 …ÇАnç. (3)
Понятие эквивалентности годится и для бесконечных множеств. Пусть, например, A = {1, 2, 3, …, n,…}, B = {– 1, –2, …, –n, …}. Тогда A ~ B. Взаимно однозначное соответствие устанавливается по правилу: элементу nÎ A соответствует элемент – nÎ B, т.е. n « – n.
Пример.
A = {1, 2, 3, …, n,…}, B = {2, 4 …, 2n, …}. Тогда A ~ B. Взаимно однозначное соответствие устанавливается по правилу: n « 2*n.
A = {1, 2, 3, …, n,…} – множество натуральных чисел, B = {…, –n, …– 2, –1, 0, 1, 2, …, n, …} – множество всех целых чисел.
Перепишем множество B следующим образом:
B = {0, –1, 1, – 2, 2, …, –n, n, …}, так, что 0 будет на первом месте, –1 на втором, 1 на третьем, –2 на четвертом и т.д. Нетрудно заметить, что отрицательные числа будут стоять на местах с четными номерами, а 0 и положительные числа – на местах с нечетными номерами. Поэтому взаимно однозначное соответствие между множествами A и B устанавливается по правилу: для всякого n ³ 0 элементу a = 2n +1 из множества A (т.е. нечетному элементу) соответствует элемент b = n из множества B; элементу a = 2n из множества A (т.е. четному элементу) соответствует элемент b = –n из множества B. Таким образом, реализуется взаимно однозначное соответствие между множествами A и B: 1 « 0, 2 « –1, 3 « 1, 4 « –2 и т.д.
Установить эквивалентность множеств, т.е. установить взаимно однозначное соответствие между их элементами можно различными способами.
Множество, эквивалентное множеству натуральных чисел N = {1, 2, 3, …, n,…}, называется счетным. Можно сказать также, что множество счетно, если его элементы можно перенумеровать.
Пример.
Установить, являются ли следующие множества счетными:
1. A1 = {–1, –2, …, – n, …};
2. A2 = {2, 22, …, 2n,…};
3. A3 = {2, 4, …, 2n,…};
4. A4 = {…, – n, …, – 1, 0, 1, …, n,…};
Решение. Чтобы установить счетность некоторого множества, достаточно указать взаимно однозначное соответствие между элементами данного множества и множества натуральных чисел. Взаимно однозначное соответствие устанавливается по следующим правилам:
· для множества A1: –n « n;
· для множества A2: 2n « n;
· для множества A3: 2*n « n;
· счетность множества A4 установлена ранее в примере.
Упорядоченной парой (x, y) называется совокупность двух элементов x и y, расположенных в определенном порядке.
Две упорядоченные пары (x, y) и (u, v) равны межу собой тогда и только тогда, когда x = u и y = v.
Например, (a, b), (1, 2), (x, 4) – упорядоченные пары.
Аналогично можно рассматривать тройки, четверки, n-ки элементов (x1, x2, … xn).
Прямым (или декартовым)произведением двух множеств A и B называется множество упорядоченных пар, таких, что первый элемент каждой пары принадлежит множеству A, а второй – множеству B:
A ´ B = {(a, b), / aÎ А и bÎ В}.
В общем случае прямым произведением n множеств А1, А2,… Аn называется множество А1 ´ А2 ´ …´ Аn, состоящее из упорядоченных наборов элементов (a1, a2, …, an) длины n, таких, что i- ый ai принадлежит множеству Аi, ai Î Аi.
Пример.
Пусть А = {1, 2}, В = {2, 3}. Тогда A ´ B = {<1, 2>, <1, 3>,<2, 2>,<2, 3>}.
Пусть А = {x / 0 £ x £ 1} и B = {y / 2 £ y £ 3}. Тогда A ´ B = {< x, y > / 0 £ x £ 1и2 £ y £ 3}. Таким образом, множество A ´ B состоит из точек, лежащих внутри и на границе прямоугольника, образованного прямыми x = 0 (ось ординат), x = 1, y = 2и y = 3.
Французский математик и философ Декарт впервые предложил координатное представление точек плоскости. Это исторически первый пример прямого произведения.