Главная | Обратная связь

Практическая работа по теме 2.

Задание 1. В группе спортсменов 30 человек. Из них 20 занимаются плаванием, 18 – легкой атлетикой и 10 – лыжами. Плаванием и легкой атлетикой занимаются 11 человек, плаванием и лыжами – 8, легкой атлетикой и лыжами – 6 человек. Сколько спортсменов занимаются всеми тремя видами спорта?

Решение. Введем следующие обозначения: П – множество спортсменов группы, занимающихся плаванием; ЛА - множество спортсменов группы, занимающихся легкой атлетикой; Л - - множество спортсменов группы, занимающихся лыжами. Тогда из условия задачи имеем:

Следовательно,

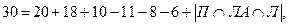
то есть

Задание 2. Найти количество целых положительных чисел, не превосходящих 1000 и не делящихся нацело ни на одно из чисел 3, 5, и 7.

Решение. Пусть А, В, С — множества целых положительных чисел, не превосходящих 1000, делящихся нацело на 3, 5, и 7 соответственно. Тогда АÇВ, АÇС, ВÇС, АÇВÇС — множества целых положительных чисел, не превосходящих 1000, делящихся нацело на15 = 3×5, 35 = 5×7, 21 = 3×7 и 105 = 3×5×7 соответственно. Тогда

Следовательно, количество целых положительных чисел, не превосходящих 1000 и не делящихся нацело ни на одно из чисел 3, 5, и 7, равно 1000 – 543 = 457.

Задание 3. Изобразить на координатной плоскости следующее множество: [4,6]´{2,1}.

Решение. По определению декартового произведения множеств запишем:

[4,6]´{2,1}={(x,y)/ xÎ[4,6]Ù yÎ{2,1}}={(x,2)/ xÎ[4,6] Ù (x,1)/ xÎ[4,6]}. Таим образом, искомое множество представляет собой два отрезка: 1-й отрезок прямой y=2 при 4£x£6; 2-й отрезок прямой y=1 при 4£x£6 (рис. 5).

Рисунок 5.

 

Задание 4. Доказать, что для любых множеств A, B и C выполняется соотношение

Решение.

1. Предположим, что для некоторого элемента x имеет место соотношение xÎ AÈ (BÇC). Докажем, что x принадлежит и правой части, т.е. xÎ(AÈB) Ç (AÈC).

xÎ AÈ (BÇC)Û xÎ AÚ xÎ(BÇC)Û xÎ AÚ (xÎBÙ xÎC) Û (xÎ AÚxÎB) Ù (xÎ AÚxÎC) Û xÎ AÈBÙ xÎ AÈCÛ xÎ (AÈB) Ç(AÈC)

Доказательство тождеств можно проиллюстрировать с помощью диаграмм Эйлера-Венна. На рис. 6 изображено формирование левой части равенства - AÈ (BÇC). На рис7 - правой части - (AÈB) Ç (AÈC).

 

 

Рисунок 6.

Рисунок 7

 

Задание 5. Доказать, что

Решение. Преобразуем левую часть равенства, учитывая, что

Задание 6. Пусть А={xÎN| 2<x£6}, B={xÎN| 1<x<4}, C={xÎN| x²-4=0}. Найти (АÇВ) ÈВÈС, С´В, В´С.

Решение. А={3, 4, 5, 6}, B={2, 3}, C={2}.

Тогда AÇB={3}, ВÈС={2, 3}, (АÇВ) ÈВÈС={2, 3}.

С´В={(2, 2), (2, 3)}, B´C={(2, 2), (3, 2)}.