Здавалка
Главная | Обратная связь

Задания для самостоятельной работы по теме 2.

⇐ ПредыдущаяСтр 13 из 31Следующая ⇒

Задание 1. Решить задачу.

1.У фирмы есть 100 предприятий, причем каждое предприятие выпускает хотя бы одну продукцию вида А, В или С. Продукцию всех трех видов выпускают 10 предприятий, продукцию вида А и В – 18 предприятий, продукцию вида А и С – 15 предприятий, продукцию вида В и С – 21 предприятие. Число предприятий, выпускающих продукцию вида А, равно числу предприятий, выпускающих продукцию вида В, и равно числу предприятий, выпускающих продукцию вида С. Найти число предприятий, выпускающих только продукцию вида А.

2.В студенческой группе 20 человек. Из них 10 имеют оценку «девять» по английскому языку, 8 – по математике, 7 – по физике, 4 – по английскому языку и по математике, 5 – по английскому языку и по физике, 4 – по математике и по физике, 3 – по английскому языку, по математике и по физике. Сколько студентов в группе не имеют оценок «девять»?

3.В классе 20 человек. На экзаменах по истории, математике и литературе 10 учеников не получили ни одной оценки «9», 6 учеников получили «9» по истории, 5 – по математике и 4 – по литературе, 2 – по истории и математике, 2 – по истории и литературе, 1 – по математике и литературе. Сколько учеников получили «9» по всем предметам?

4.В спортивном лагере 100 человек, занимающихся плаванием, легкой атлетикой и лыжами. Из них 10 занимаются и плаванием, и легкой атлетикой, и лыжами, 18 – плаванием и легкой атлетикой, 15 – плаванием и лыжами, 21 – легкой атлетикой и лыжами. Число спортсменов, занимающихся плаванием, равно числу спортсменов, занимающихся легкой атлетикой, и равно числу спортсменов, занимающихся лыжами. Найти это число.

5.Группе студентов предложены спецкурсы по мультимедиа, искусственному интеллекту и имитационному моделированию. 22 студента записались на спецкурс по мультимедиа, 18 – на спецкурс по искусственному интеллекту, 10 – на спецкурс по имитационному моделированию, 8 – на спецкурсы по мультимедиа и искусственному интеллекту, 15 – на спецкурсы по мультимедиа и имитационному моделированию, 7 – на спецкурсы по искусственному интеллекту и имитационному моделированию. 5 студентов записались на все три спецкурса. Сколько студентов в группе?

6.Во время сессии 24 студента группы должны сдать три зачета: по физике, математике и программированию. 20 студентов сдали зачет по физике, 10 – по математике, 5 – по программированию, 7 – по физике и математике, 3 – по физике и программированию, 2 – по математике и программированию. Сколько студентов сдали все три зачета?

7.В группе переводчиков 15 человек владеют английским языком, 19 – французским, 8 – немецким. 9 переводчиков владеют английским и французским языками, 7 – английским и немецким, 6 – французским и немецким. 4 переводчика владеют всеми тремя языками. Сколько переводчиков в группе?

8.Опрос группы студентов показал, что 70 % из них любят ходить в кино, 60 % – в театр, 30 % – на концерты. В кино и театр ходят 40 % студентов, в кино и на концерты – 20 %, в театр и на концерты – 10 %. Сколько студентов (в %) ходят в кино, театр и на концерты?

9.В группе 20 студентов. После медицинского осмотра 14 студентов были направлены на дополнительное обследование к терапевту, 6 – к окулисту, 5 – к ортопеду. К терапевту и окулисту были направлены 3 студента, к терапевту и ортопеду – 3, к окулисту и ортопеду – 2. Сколько студентов было направлено к терапевту, окулисту и ортопеду?

10. При обследовании рынка спроса инспектор указал в опросном листе следующие данные. Из 1000 опрошенных 811 покупают жевательную резинку «Dirol», 752 – «Orbit» , 418 – «Stimorol», 570 – «Dirol» и «Orbit», 356 – «Dirol» и «Stimorol», 348 – «Orbit» и «Stimorol», 297 – все виды жевательной резинки. Не ошибся ли инспектор?

11. Всем участникам автопробега не повезло. 12 из них увязли в песке – пришлось толкать машину, 8 понадобилась замена колеса, у шестерых перегрелся мотор, пятеро толкали машину и меняли колесо, четверо толкали машину и остужали мотор, трое меняли колесо и остужали мотор. Одному пришлось испытать все виды неполадок. Сколько всего было участников автопробега?

12. В цеху имеется 25 станков, которые могут выполнять три вида операций: А, В и С. Из них 10 станков выполняют операцию А, 15 – В, 12 – С. Операции А и В могут быть выполнены на 6 станках, А и С – на 5, В и С – на 3 станках. Сколько станков могут выполнять все три операции?

Задание 2. Изобразить на координатной плоскости следующие множества:

1. ; 2. {6}´(0,2);
3. {2}´R; 4. [-1,1]2;
5. (1,4) ´ R; 6. {3}´[3,5]

 

Задание 3. Определить, эквивалентны ли следующие множества:

1. и ;

2. и ;

3. и ;

4. A = { 2n, n = 1, 2, …} и B = {n2, n = 1, 2, …};

5. A = {y / y = 3x, 0<x< ¥} и B = {y / y = 3n, n = 1, 2, …}?

Задание 4. Установить, имеют ли место равенства:

1. 7.
2. 8.
3. 9.
4. 10.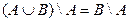
5. 11.
6. 12.

 

Задание 5. Заданы множества А, B, С. Найти (АÇВ) ÈВÈС, С´В, В´С, А2, А´В, В2.

1. А={1, 2, 3}; B={1, 2, 3, 4, 5, 6}; C={2, 3}.

2. А={1, 3}; B={4, 5, 6}; C={2, 3, 4}.

3. А={1, 2, 3, 4, 5, 6}; B={1, 2, 3}; C={2, 3}.

4. А={1, 5, 6}; B={2, 3, 4}; C={7, 8}.

 

 

Контрольные вопросы по теме 2.

  1. Пусть a Î А. Следует ли отсюда, что {a} 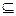А?
  2. В каком случае А 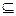АÇВ?
  3. Назовите множество, которое является подмножеством любого множества.
  4. Может ли быть множество эквивалентно своему подмножеству?
  5. Упростить:
    • (AÇB) È (AÇB).
    • (AÈB) È(AÈB)
    • Ç ( È ).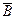
    • (A Ç С )\ (С Ç (A ÈB))
  6. Является ли множество А = {1, 2, 3} подмножеством множества В = {{1}, {2, 3}}?
  7. Найти все подмножества множества A= {x, y, z}.
  8. Нарисовать диаграмму Эйлера-Венна для заданного множества
    • (А \ В) Ç С
    • (А \ В) È С
    • ( È 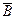) \ (A È B).
    • (A Ç B) È (C \ (A È B)).
    • ÇС
    • А Ç (В È ).
    • \ .
  9. Найти все подмножества множества A= {1, 2, 3, 4).
  10. Придумать пример множеств А, В, С, так, чтобы выполнялось равенство: А È В = С, причем А – конечное множество, В и С – счетные множества.
  11. Пусть A – множество целых чисел, а B – множество четных чисел. Какие из следующих отношений справедливы: а) A =B; б) A ~ B; в) A É B; г) A Ê B; д) A Ë B.
  12. Придумать пример множеств А, В, С, так, чтобы выполнялось равенство: А È В = С, причем А, В, и С – счетные множества.
  13. Пусть A – множество точек отрезка [0, 1], а B – множество всех точек числовой оси. Какие из следующих отношений справедливы: а) A =B; б) A ~ B; в) A É B; г) A Ê B; д) A Ë B.
  14. Пусть A – множество решений уравнения x2 – 3x + 2 = 0. Записать это множество двумя различными способами.
  15. Привести примеры множеств А, В и С , для которых одновременно выполняются равенства А È В È С = А и А Ç В Ç С = С.
  16. Привести примеры множеств А и В, для которых равенство È В =

а) выполняется; б) не выполняется.

  1. Привести примеры множеств А, В и С так, чтобы A Ì B, В Ì С.
  2. Можно ли утверждать, что множество всех положительных пятизначных чисел счетно? Ответ обосновать.
  3. Можно ли утверждать, что множество всех положительных чисел имеет меньшую мощность, чем множество всех действительных чисел? Ответ обосновать.

 

⇐ Предыдущая891011121314151617Следующая ⇒






©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов.