Главная | Обратная связь

Тема 3. Отношения. Функции.

Основные понятия и определения

С понятием отношения между объектами мы встречаемся повсюду, как в математике, так и в жизни. Не давая пока точных определений, рассмотрим некоторые примеры отношений.

1) Пусть X — множество всех людей, а Y — множество всех городов нашей страны в данный момент и пусть xÎX и yÎY. Тогда можно поставить вопрос: в каком отношении нахъодится х к у? В зависимости от того, кто такой х и что за город у, ответы могут быть разными: «х живет в y», «x родился в у», «х работает в у», «х учится в у» и т. д. Каждый из этих ответов представляет собой двухместный, предикат, определенный на декартовом произведении X´Y и задает вполне определенное отношение между отдельными элементами данных множеств. Очевидно, что совокупность всех пар (х; у), для которых истинно, например, утверждение «х живет в у», представляет собой подмножество декартова произведения X´Y и в то же время является областью истинности предиката «х живет в у».

2) Можно говорить и об отношениях между элементами одного и того же множества. Пусть, например, X — множество прямых на плоскости и пусть a, bÎХ. Тогда можно ввести такие отношения между а и b: «а параллельно b», «а пересекает b», «а перпендикулярно b» и т. д. При этом, очевидно, что

{(а; b) / а || b} Ì X², {(а; b) / а ^b} Ì X² и т . д .

Пусть теперь X и Y — два произвольных множества. Тогда отношение между элементами х и у (xÎX и yÎY) принято обозначать буквами R, S, T, f, p, g и т. д. При этом записи xRy (xTy, xfy и т. д.) означают, что «элемент х находится в отношении R (T, f, g и т. д.) к элементу у».

Пусть R — произвольное отношение между элементами множеств X и Y. Тогда множество всех пар (х; у) Î X´Y, для которых предикат xRy превращается в истинное высказывание, будем называть графиком отношения R и обозначать G_R. Таким образом

G_R = {(x;y) Î X´Y / xRy} (1)

Из равенства (1) видно, что G_R Ì X´Y и что G_R — область истинности двухместного предиката xRy.

Из рассмотренных примеров следует, что каждое отношение R между двумя объектами xÎX и yÎY связано с тремя множествами: X, Y и G_R, где G_R Ì X´Y. Поэтому можно сформулировать следующее определение отношения между двумя множествами:

Отношением (или соответствием) между двумя множествами X и Y называется тройка множеств (X, У, G), где Г — некоторое подмножество декартова произведения X´Y, т. е. R: =(Х; У; Г), где ГÌ X´Y.

При этом принято говорить, что X — область отправления отношения R, Y — область прибытия отношения R, Г — график отношения R. Совокупность первых (вторых) компонент пар (x;y) ÎG_R называют областью определения (множеством значений) отношения R и обозначают D_R (E_R). То есть:

D_R={xÎX / $yÎY Ù xRy};

E_R={yÎY / $xÎX Ù xRy}.

Ясно, что D_RÌX, E_RÌY.

Из равенства (1) имеем, что (x;y) ÎG_RÛxRy.

Если задано отношение R = (X; Y; Г) и если (x;y) ÎG_R (или xRy), то говорят, что отношение R элементу х ставит в соответствие элемент у, или что элементу х соответствует элемент у в силу отношения R.

Если (x₀, y₀) ÎG_R, то элементу x₀ может соответствовать не только элемент y₀, но и некоторые другие элементы из Y. Совокупность всех элементов y ÎY, для которых (x₀, y) ÎG_R называют полным образом элемента x₀ при отношении R и обозначают R(х₀). Таким образом, " x₀ÎX R(х₀)ÌY и y₀ Î R(х₀)Û x₀RyÛ(x₀, y) ÎG_R, то есть
R(х₀)={yÎY/Û(x₀, y) ÎG_R}.

Примеры.

1. Пусть X = {10; 20; 30; 40}, Y = {2; 3; 4} и пусть отношение R между этими множествами задано в виде: «x делится на у», где хÎХ, yÎY. Тогда имеем:

Г_R = {(10; 2); (20; 2); (30; 2); (40; 2); (20; 4); (40; 4); (30; 3)};

D_R = X; E_R = Y; R (10) = {2}; R (20) = {2; 4}; R (30) = {2;3}; R(40) = {2; 4}.

2. Для тех же множеств, что и в примере 1 зададим такое отношение S: «при делении х на у в остатке получается 2». Тогда G_S ={(20;3); (10;4); (30; 4)}, D_S = {10; 20; 30}¹X; E_S = {3; 4}¹Y; S (20) = {3}; S (10) = (4}; S (30) = {4}, S (40) = Æ.

Пусть задано отношение R = (X; Y; Г_R)_.между множествами X и Y. Тогда отношение R^-1 = (Y; X; Г_R) между множествами Y и X называется обратным к отношению R, если

,

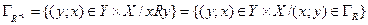а отношение противоположным отношению R, если .

Из данного определения видно, что .