Главная | Обратная связь

Отношение эквивалентности.

Отношение R называется отношением эквивалентности на множестве X, если оно рефлексивно, симметрично и транзитивно на множестве X.

Пример.

а) Пусть X – конечное множество, X = {1, 2, 3} и r = {(1, 1), (2, 2), (3, 3)}. Отношение R является отношением эквивалентности.

б) Пусть X – множество действительных чисел и R отношение равенства. Это отношение эквивалентности.

в) Пусть X – множество студентов и R отношение "учиться в одной группе". Это отношение эквивалентности.

Пусть R – отношение эквивалентности на множестве X.

Пусть R – отношение эквивалентности на множестве X и xÎ X. Классом эквивалентности, порожденным элементом x, называется подмножество множества X, состоящее из тех элементов y Î X, для которых xRy. Класс эквивалентности, порожденный элементом x, обозначается через [x]. Таким образом, [x] = {yÎ X / xRy}.

Классы эквивалентности образуют разбиение множества X, т. е. систему непустых попарно непересекающихся его подмножеств, объединение которых совпадает со всем множеством X.

Пример.

а) Отношение равенства на множестве целых чисел порождает следующие классы эквивалентности: для любого элемента x из этого множества [x] = {x}, т.е. каждый класс эквивалентности состоит из одного элемента.

б) Класс эквивалентности, порожденный парой (x, y) определяется соотношением:

[(x, y)] = .

Каждый класс эквивалентности, порожденный парой (x, y), определяет одно рациональное число.

в) Для отношения принадлежности к одной студенческой группе классом эквивалентности является множество студентов одной группы.

Отношение R называется отношением частичного порядка (или просто частичным порядком) на множестве X, если оно рефлексивно, антисимметрично и транзитивно на множестве X. Множество X в этом случае называют частично упорядоченным и указанное отношение часто обозначают символом £, если это не приводит к недоразумениям.

Отношение, обратное отношению частичного порядка будет, очевидно, отношением частичного порядка.

Пример.

а) Пусть X – конечное множество, X = {1, 2, 3} и r = {(1, 1), (1, 2), (1, 3), (2, 2), (2, 3), (3, 3)}. Отношение R есть отношение частичного порядка.

б) Отношение А Í В на множестве подмножеств некоторого множества U есть отношение частичного порядка.

в) Отношение делимости на множестве натуральных чиселесть отношение частичного порядка.

Композицией двух отношений r и s называется отношение

s r = {(x, z) ç 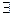y, что (x, y) Î r и ( y, z) Îs}.

Пример.

r = {(x, y) / y = sinx}.

s = {(x, y) /y = Öx}.

s r = {(x, z) / 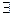y/ (x, y) Î r и ( y, z) Îs} = {(x, z) / 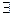y = sinx и z = Öy} = {(x, z) / z = Ösinx}.

Определение композиции двух отношенийсоответствует определению сложной функции.

 

Функции. Основные понятия и определения

Рассмотрим определение функции с точки зрения отношений.

Отношение f между двумя произвольными множествами X и Y называется функцией (или отображением) из X в Y, если оно каждому элементу множества X ставит в соответствие не более одного элемента из Y, т. е. если "xÎD_f f(x) — одноэлементное множество. Это обозначается записью y = f(x). Элемент x называется аргументом функции или прообразом элемента y при функции f, а элемент y значением функции f на x или образом элемента x при f.

Такое свойство отношения называется однозначностью или функциональностью.

Пример.

а) {(1, 2), (3, 4), (4, 5), (5, 6)} – функция.

б) {(x, y) / x, y Î R ˄ y = x²} – функция.

в) {(1, 2), (1, 4), (4, 4), (5, 6)} – отношение, но не функция.

Функции f и g равны, если их область определения – одно и то же множество D, и для любого x Î D справедливо равенство f(x) = g(x).

Функция (отображение) f называется сюръективной или просто сюръекцией, если для любого элемента y Y существует элемент x Î X, такой, что y = f(x). Таким образом, каждая функция f является сюръективным отображением (сюръекцией) D_f ® R_f.

Если f – сюръекция, а X и Y – конечные множества, то ³ .

Функция (отображение) f называется инъективной или просто инъекцией или взаимно однозначной, если для любых значений a и b из области определения из того, что выполняется условие f(a) = f(b), следует что a = b.

Функция (отображение) f называется биективной или просто биекцией, если она одновременно инъективна и сюръективна.

Если f – биекция, а X и Y – конечные множества, то = .

Пример.

а) f(x) = x² есть отображение множества действительных чисел на множество неотрицательных действительных чисел. Т.к. f(–a) = f(a), и a ¹ –a, то эта функция не является инъекцией.

б) Для каждого x R = (– , ) функция f(x) = 5 – функция-константа. Она отображает множество R на множество {5}. Эта функция сюръективна, но не инъективна.

в) f(x) = 2x + 1 на множестве R является сюръекцией, т.к. для любого действительного числа y существует элемент x, такой что y=f(x) = 2x + 1; инъекцией, т.к. из 2x₁ +1 = 2x₂ +1 следует, что x₁ = x₂. Следовательно заданная функция является биекцией.