Главная | Обратная связь

Практическая работа по теме 3.

Задание 1. Задано отношение r={(x, y)/x*y>1} на множестве R . Найти D_r, E_r, G_r, r ^-1. Определить, какими свойствами обладает отношение.

Решение. Для заданного отношения D_r=(0; +µ), E_r=(0; +µ), G_r={(x, y)/x*y>1}={(x, y)/y>1/x}.

Проверим свойства отношения.

Рефлексивность: "xÎ D_r/xrx Û (x, x) Î rÛx*x>1 – не выполняется. Следовательно, отношение не рефлексивно.

Симметричность: "x,yÎ D_r/x*y>1Þy*x>1 – выполняется в силу коммутативности операции умножения. Следовательно, отношение симметрично.

Так как выполняется симметричность, то асимметричность и антисимметричность не проверяем.

Транзитивность: "x, y, zÎ D_r (x*y>1 Ù y*z>1Þx*z>1) – не выполняется. Следовательно, отношение не транзитивно.

 

Задание 2. Доказать, что заданное отношение r является отношением эквивалентности.

r={(x, y)/x-y делится на m} на множестве Z, mÎN.

Решение. Для доказательства того, что отношение является отношением эквивалентности, необходимо проверить выполнение свойств рефлективности, симметричности и транзитивности.

Рефлексивность: "xÎ D_r/xrx Û x-x=0=0*mÞ$ mÎZ / (x, x) Î r. Следовательно, отношение рефлексивно.

Симметричность: "x,yÎ D_r/ x-y делится на m Þ y-x делится на m

Пусть (x,y)Î r Þ$ kÎZ / x-y=k*m Þ$ kÎZ / y-x=-k*mÞ"(y, x)Î r.

Следовательно, отношение симметрично.

Транзитивность: "x, y, zÎ D_r ((x-y делится на m) Ù (y-z делится на m) Þ (x-z делится на m)).

Пусть (x,y)Î r Ù(y,z)Î r Þ$k, nÎZ / x-y=k*m Ù y-z=n*m Þ
$k, nÎZ / (x-z) = (k+n)*m Þ $r=(k+n) ÎZ / x-z=r*mÞ(x,z)Î r.

Следовательно, отношение транзитивно.

Таким образом, заданное отношение является отношением эквивалентности.

 

Задание 3. Дана функция f(x), отображающая множество [0; 1] во множество [0; 3]. Является ли эта функция сюръективной, инъективной, биективной?

1. f(x) = ;

2. f(x)=3^x;

3. f(x)= .

Решение.

1. Для произвольного yÎ[0; 3] уравнения y = имеем единственное решение , принадлежащее [0; 1]. Следовательно функция является инъективной и сюръективной, а значит и биективной.

2. Если yÎ[0; 3], то уравнение y=3^x имеет не более одного решения xÎ [0; 1]. При yÎ[1; 3] решением является x=log₃y, а при yÎ[0; 1] решений нет. Следовательно, функция инъективна.

3. Из уравнения y= , yÎ[0; 3] находим при чем, если 0£y£3, то оба корня лежат в интервале (0, 1]; если y=0, то корни совпадают 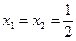и принадлежат отрезку [0; 1]. Следовательно, для всех yÎ[0; 3] уравнение y= на [0; 1] имеет хотя бы одно решение. Поэтому рассматриваемая функция сюръективна.