 |
|
Метод итерации для нелинейной системы уравнений
Пусть требуется найти действительные решения системы двух уравнений с заданной точностью
 .
.
Для этого перепишем исходную систему в приведенном (итерационном) виде:  . Пусть
. Пусть  и
и 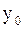 – начальные приближения корней, полученные графическим или каким-либо другим способом. Подставив эти значения в правые части приведенной системы уравнений, можно получить
– начальные приближения корней, полученные графическим или каким-либо другим способом. Подставив эти значения в правые части приведенной системы уравнений, можно получить
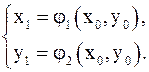
Аналогично можно получить второе приближение 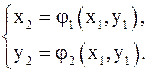
В общем случае  Если функции
Если функции  и
и 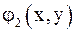
непрерывны и последовательности  и
и 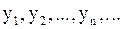 сходятся, то пределы их дают решение приведенной, следовательно, и исходной системы.
сходятся, то пределы их дают решение приведенной, следовательно, и исходной системы.
Сходимость метода
Теорема.Пусть в некоторой замкнутой окрестности  имеется одно и только одно решение
имеется одно и только одно решение  и
и  приведенной системы.
приведенной системы.
Тогда если:
1) функции  и
и 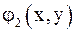 определены и непрерывно дифференцируемы в
определены и непрерывно дифференцируемы в  ;
;
2) начальные приближения  ,
, 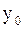 и все последующие приближения
и все последующие приближения  ,
,  принадлежат
принадлежат  ;
;
3) в  выполнены неравенства
выполнены неравенства  или
или
неравенства  ,то процесс последовательных приближений сходится к решению
,то процесс последовательных приближений сходится к решению ,
,  .
.
Оценка погрешности  -го приближения определяется неравенством:
-го приближения определяется неравенством:
 ,
,
где 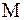 – наибольшее из чисел
– наибольшее из чисел  и
и  , входящих в эти неравенства.
, входящих в эти неравенства.
Сходимость метода считается хорошей, если 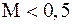 ; при этом
; при этом  . Поэтому если в двух последовательных приближениях совпадают, например, три десятичных знака после запятой, то ошибка последнего приближения не превосходит 0,001.
. Поэтому если в двух последовательных приближениях совпадают, например, три десятичных знака после запятой, то ошибка последнего приближения не превосходит 0,001.
Пример.Методом итерации решить систему с точностью до  .
.
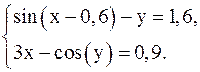
Решение.
1) Приведем систему к форме: 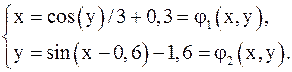
2) Для нахождения начального приближения отделим корни. Построив два графика  и
и  и найдя их точку пересечения, можно увидеть, что система имеет единственное решение, заключенное в области
и найдя их точку пересечения, можно увидеть, что система имеет единственное решение, заключенное в области 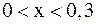 и
и  .
.
3) Проверим приведенную систему на сходимость итерационного процесса:
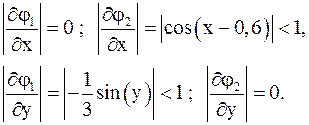
Следовательно,
 и
и 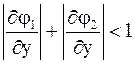 т.е. условия сходимости выполняются.
т.е. условия сходимости выполняются.
4) Для поиска последовательных приближений используют формулы:
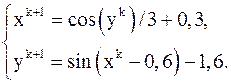
Выберем следующие начальные значения: 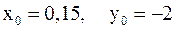 .
.

| 0,15 | 0,1616 | 0,1508 | 0,1539 | 0,1510 | 0,1519 | 0,1510 |

| -2 | -2,035 | -2,0245 | -0,0342 | -2,0313 | -2,0341 | -2,0333 |
Поскольку  , то
, то  и
и 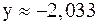 .
.