Главная | Обратная связь

Модифицированные методы Эйлера

Первый модифицированный метод Эйлера. Суть этого метода состоит в следующем. Сначала вычисляются вспомогательные значения искомой функции в точках с помощью формулы:

.

Затем находится значение правой части исходного уравнения в средней точке и затем полагается , .

Эти формулы являются расчетными формулами первого модифицированного метода Эйлера.

Первый модифицированный метод Эйлера является одношаговым методом

со вторым порядком точности.

Второй модифицированный метод Эйлера – Коши.Суть этого метода состоит в следующем. Сначала вычисляются вспомогательные значения

.

Затем приближения искомого решения находятся по формуле:

.

Эти формулы являются расчетными формулами второго модифицированного метода Эйлера – Коши.

Второй модифицированный метод Эйлера – Коши так же, как и первый, является одношаговым методом со вторым порядком точности.

Оценка погрешности.Приближенная оценка погрешности модифицированных методов Эйлера осуществляется как и для простого метода Эйлера с использованием правила Рунге. Так как оба модифицированных метода Эйлера имеют второй порядок точности, т. е. , то оценка погрешности примет вид: .

Используя правило Рунге, можно построить процедуру приближенного вычисления решения задачи Коши модифицированными методами Эйлера с заданной точностью . Нужно, начав вычисления с некоторого значения шага , последовательно уменьшать это значение в два раза, каждый раз вычисляя приближенное значение . Вычисления прекращаются тогда, когда будет выполнено условие: .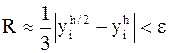

Приближенным решением будут значения .

Пример 2.Применим первый модифицированный метод Эйлера для решения задачи Коши , рассмотренной ранее в предыдущем примере. Возьмем шаг . Тогда , и расчетная формула первого модифицированного метода Эйлера имеет вид: , где

, ,

, .

Решение представим в виде таблицы 7.

Таблица 7

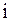
			0,1	0,1	1,1	0,1836
	0,2	1,1836	0,0850	0,3	1,2682	0,1590
	0,4	1,3426	0,0747	0,5	1,4173	1,1424
	0,6	1,4850	0,0677	0,7	1,5527	0,1302
	0,8	1,6152	0,0625	0,9	1,6777	0,121
		1,7362

 

Третий столбец таблицы 3 содержит приближенное решение . Сравнивая полученное приближенное решение с точным решением, представленном в таблице 2, видим, что погрешность составляет

.

Пример 3.Применим второй модифицированный метод Эйлера – Коши для решения задачи Коши , рассмотренной ранее в примерах 1 и 2. Так же, как и ранее, зададим шаг . Тогда

.

В соответствии с данными формулами получим расчетную формулу метода Эйлера – Коши:

,

где , , , , .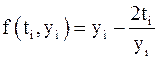

Решение представим в виде таблицы 8.

 

Таблица 8

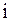
			0,1	0,2	1,2	0,867
	0,2	1,1867	0,0850	0,4	1,3566	0,767
	0,4	1,3484	0,0755	0,6	1,4993	0,699
	0,6	1,4938	0,0690	0,8	1,6180	0,651
	0,8	1,6272	0,0645		1,7569	0,618
		1,7542

 

Таблица 8 заполняется последовательно по строкам, сначала первая строка, затем вторая и т. д. Третий столбец таблицы 8 содержит приближенное решение .

Сравним полученное приближенное решение с точным решением, представленном в таблице 7. Видим, что погрешность составляет .