|
|
УРАВНЕНИЯ ПРЯМОЙ В ПРОСТРАНСТВЕ
| Название | Уравнение | Обозначения |
| 1. Общее уравнение | 
|  -
нормальные векторы плоскости. -
нормальные векторы плоскости.
|
| 2. Каноническое | 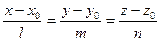
|  - направляющий вектор. - направляющий вектор.
|
| 3. Параметрическое | 
|  - точка на прямой. - точка на прямой.
 - направляющий вектор. - направляющий вектор.
|
| 4. Уравнение прямой, проходящей через две точки М1 и М2 | 
| 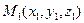 и и  - точки на прямой - точки на прямой
|
УРАВНЕНИЯ ПРЯМОЙ НА ПЛОСКОСТИ
| Название | Уравнение | Обозначения |
| 1. Уравнение плоскости, проходящей через точку М0 | 
|  - точка на плоскости - точка на плоскости
 - нормальный вектор прямой. - нормальный вектор прямой.
|
| 2. Общее | 
|  - нормальный вектор плоскости. - нормальный вектор плоскости.
|
| 3. Проходящей через точки: М1, М2, | 
|  , ,  и
- заданные точки прямой. и
- заданные точки прямой.
|
| 4. В отрезках | 
| a, b – отрезки на соответствующих осях. |
| 5. Нормальное уравнение | 
|  - нормальный вектор прямой. - нормальный вектор прямой.
|
| 6. Расстояние от точки до прямой | 
|
УРАВНЕНИЯ ПЛОСКОСТИ
| Название | Уравнение | Обозначения |
| 1. Уравнение плоскости, проходящей через точку М0 | 
|  - точка на плоскости - точка на плоскости
 - нормальный вектор плоскости. - нормальный вектор плоскости.
|
| 2. Общее | 
|  - нормальный вектор плоскости. - нормальный вектор плоскости.
|
| 3. Проходящее через три точки: М1, М2, М3 | 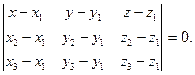
| 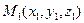 , ,  и и
 - заданные точки плоскости - заданные точки плоскости
|
| 4. В отрезках | 
| a, b, c – отрезки на соответствующих осях. |
| 5. Нормальное уравнение | 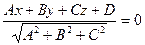
|  - нормальный вектор плоскости. - нормальный вектор плоскости.
|
| 6. Расстояние от точки до плоскости | 
|
Вывод уравнения плоскости:
 | |||
 | |||
|
|

| |||||
 | |||||
|
Задания для самостоятельной работы.
Задание 1. Исследовать данную систему и в случае совместности
уравнений системы решить ее методом Гаусса.
| 1.1. | 
| 1.2. | 
|
| 1.3. | 
| 1.4. | 
|
| 1.5. | 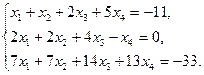
| 1.6. | 
|
| 1.7. | 
| 1.8. | 
|
| 1.9. | 
| 1.10. | 
|
| 1.11. | 
| 1.12. | 
|
| 1.13. | 
| 1.14. | 
|
| 1.15. | 
| 1.16. | 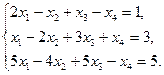
|
| 1.17. | 
| 1.18. | 
|
| 1.19. | 
| 1.20. | 
|
Задание 2. Решить данное матричное уравнение.
| 2.1. | 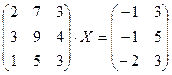
| 2.2. | 
|
| 2.3. | 
| 2.4. | 
|
| 2.5. | 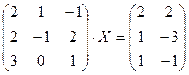
| 2.6. | 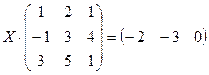
|
| 2.7. | 
| 2.8. | 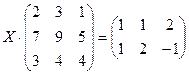
|
| 2.9. | 
| 2.10. | 
|
| 2.11. | 
| 2.12. | 
|
| 2.13. | 
| 2.14. | 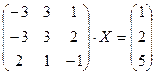
|
| 2.15. | 
| 2.16. | 
|
| 2.17. | 
| 2.18. | 
|
| 2.19. | 
| 2.20. | 
|
Задание 3. По координатам точек А, В и С для указанных векторов найти: а) модуль вектора а; б) проекцию вектора с на вектор d; в) координаты точки М, делящей отрезок АВ пополам.
3.1. А(4, 6, 3), В(-5, 2, 6), С(4, -4, -3), а = 4СВ – АС, с = СВ, d = АС.
3.2. А(4, 3, 2), В(-3, -1, 4), С(2, 2, 1), а = -5АС + 2СВ, с = АС, d = СВ.
4.3. А(-2, -2, 4), В(1, 3, -2), С(1, 4, 2), а = 2АС - 3ВА, с = СВ, d = АС.
3.4. А(2, 4, 3), В(3, 1, -4), С(-1, 2, 2), а = 2ВА + 4АС, с = ВА, d = АС.
3.5. А(2, 4, 5), В(1, -2, 3), С(-1, -2, 4), а = 3АВ - 4АС, с = ВС, d = АВ.
3.6. А(-1, -2, 4), В(-1, 3, 5), С(1, 4, 2), а = 3АС – 7ВС, с = АВ, d = АС.
3.7. А(1, 3, 2), В(-2, 4, -1), С(1, 3, -2), а = 2АВ + 5СВ, с = АС, d = АВ.
3.8. А(2, -4, 3), В(-3, -2, 4), С(0, 0, -2), а = 3АС - 4СВ, с = АВ, d = СВ.
3.9. А(3, 4, -4), В(-2, 1, 2), С(2, -3, 1), а = 5СВ + 4АС, с = ВА, d = АС.
3.10. А(0, 2, 5), В(2, -3, 4), С(3, 2, -5), а = -3АВ + 4СВ, с = АС, d = АВ.
3.11. А(-2, -3, -4), В(2, -4, 0), С(1, 4, 5), а = 4АС - 8ВС, с = АВ, d = ВС.
3.12. А(-2, -3, -2), В(1, 4, 2), С(1, -3, 3), а = 2АС - 4ВС, с = АВ, d = АС.
3.13. А(5, 6, 1), В(-2, 4, -1), С(3, -3, 3), а = 3АВ - 4ВС, с = АС, d = АВ.
3.14. А(10, 6, 3), В(-2, 4, 5), С(3, -4, 6), а = 5АС - 2СВ, с = ВА, d = АС.
3.15. А(3, 2, 4), В(-2, 1, 3), С(2, -2, 1), а = 4ВС – 3АС, с = АС, d = ВС.
3.16. А(-2, 3, 4), В(3, -1, 2), С(4, 2, 4), а = 7АС + 4СВ, с = АВ, d = СВ.
3.17. А(4, 5, 3), В(-4, 5, 3), С(5, -6, -2), а = 9АВ - 4ВС, с = АС, d = СВ.
3.18. А(2, 4, 6), В(-3, 5, 1), С(4, -5, 4), а = -6ВС + 2ВА, с = СА, d = ВА.
3.19. А(-4, -2, -5), В(3, 7, 2), С(4, 6, -3), а = 9ВА + 3ВС, с = АС, d = ВС.
3.20. А(5, 4, 4), В(-5, 2, 3), С(4, 2, -5), а = 11АС – 6АВ, с = АВ, d = АС.
Задание 4.
4.1 Даны вершины треугольника А(1,-1,2), В(5,-6,2) и С(2,3,-1). Вычислить длину его высоты, проведенной из вершины В на сторону АС.
4.2. Вычислить площадь треугольника с вершинами в точках А(1,3,-1), В(1,-1,3), С(5,-6,2).
4.3. Дана пирамида с вершинами в точках А1(3,1,4), А2(-1,6,1), А3(-1,1,6), А4(0,4,-1). Найти длину высоты, проведенной из вершины А4 на грань А1 А2 А3.
4.4. Найти площадь параллелограмма, построенного на векторах 
4.5. Вычислить любую высоту параллелепипеда, построенного на векторах
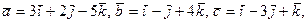 .
.
4.6. Вершины треугольной пирамиды находятся в точках А(0,0,0), В(3,4,-1), С(2,3,5), Д(6,0,-3). Найти длину высоты, проведенной из вершины С.
4.7. Найти вектор  , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям:  ортогонален векторам
ортогонален векторам  тройка векторов
тройка векторов 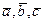 правая.
правая.
4.8. Найти координаты вектора 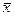 , если он ортогонален векторам
, если он ортогонален векторам
 и
и 
4.9. Даны векторы  Найти проекцию вектора
Найти проекцию вектора  +
+  на направление вектора
на направление вектора  .
.
4.10. Вектор  , коллинеарный вектору
, коллинеарный вектору 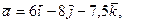 образует острый угол с осью 0Z. Найти координаты вектора
образует острый угол с осью 0Z. Найти координаты вектора  , если
, если 
4.11. Доказать, что точки А(0,1,5), В(2,1,3), С(-1,2,1), Д(1,2,-1) лежат в одной плоскости.
4.12. .При каком значении коэффициента  векторы
векторы  и
и  будут коллинеарны, если
будут коллинеарны, если 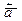 и
и  неколлинеарны?
неколлинеарны?
4.13. Найти единичный вектор 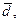 компланарный векторам
компланарный векторам  и ортогональный вектору
и ортогональный вектору  =(1,1,1).
=(1,1,1).
4.14. Вершины треугольной пирамиды находятся в точках А(0,0,0), В(3,4,-1), С(2,3,5), Д(6,0,-3). Найти длину высоты, проведенной из вершины А.
4.15. Вычислить высоту параллелепипеда, построенного на векторах 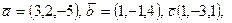 если за основание взят параллелограмм, построенный на векторах
если за основание взят параллелограмм, построенный на векторах  и
и  .
.
4.16. Найти проекцию вектора  на направление вектора
на направление вектора  = (2,2,1).
= (2,2,1).
4.17. Дана треугольная пирамида с вершинами А(0,0,1), В(2,3,4), С(6,2,3) и Д(3,7,2). Найти длину высоты пирамиды, проведенной на грань ВСД.
4.18. Дана треугольная пирамида с вершинами А(0,0,1), В(2,3,4), С(6,2,3) и Д(3,7,2). Найти длину высоты пирамиды, проведенной на грань АСД.
4.19. Как расположены точки А(0,1,5), В(2,1,3), С(-1,2,1), Д(1,2,0)? Лежат ли они в одной плоскости?
4.20. Даны векторы 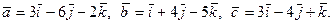 Найти проекцию вектора
Найти проекцию вектора  +
+  на направление вектора
на направление вектора  .
.
Задание 5.Даны векторы а, в, с: а) вычислить смешанное произведение трех векторов; б) найти модуль векторного произведения; в) вычислить скалярное произведение двух векторов; г) проверить, будут ли коллинеарны или ортогональны два вектора; д) проверить, будут ли компланарны три вектора.
5.1. а = 2i - 3j + k, в = j + 4k, с = 5i + 2j -3k;
а) а, 3в, с; б) 3а, 2с; в) –4с, в; г) а, с; д) а, 2в, 3с.
5.2. а = 3i + 4j + k, в = i - 2j + 7k, с = 3i -6j + 21k;
а) 5а, 2в, с; б) 4в, 2с; в) с, а; г) в, с; д) 2а, -3в, с.
5.3. а = 2i - 4j - 2k, в =7i + 3j, с = 3i + 5j -7k;
а) а, 2в, 3с; б) 3а, -7в; в) с, -2а; г) а, с; д) 3а, 2в, 3с.
5.4. а = -7i + 2k, в =2i - 6j +4k, с = i - 3j + 2k;
а) а, -2в, -7с; б) 3с, 4в; в) -7с, 2а; г) в, с; д) 2а, 4в, 3с.
5.5. а = -4i + 2j - k, в = 3i +5j - 2k, с = j +5k;
а) а, 6в, 3с; б) а, 2в; в) –4с, а; г) а, в; д) а, 6в, 3с.
5.6.а = 3i - 2j + k, в = 2j - 3k, с = -3i + 2j - k;
а) а, -3в, 2с; б) 5а, 3с; в) –2а, в; г) а, с; д) 5а, 4в, 3с.
5.7. а = 4i - j + 3k, в = 2i + 3j - 5k, с = 7i + 2j + 4k;
а) 7а, -4в, 2с; б) 3а, 5с; в) 4с, 2в; г) в, с; д) 7а, 2в, 5с.
5.8. а = 4i + 2j - 3k, в = 2i + k, с = -12i - 6j + 9k;
а) 2а, 3в, с; б) 4а, 3в; в) -4с, в; г) а, с; д) 2а, 3в, -4с.
5.9. а = -i + 5k, в = -3i +2j + 2k, с = -2i - 4j + k;
а) 3а, -4в, 2с; б) 7а, -3с; в) 4в, 3а; г) в, с; д) 7а, 2в, -3с.
5.10. а = 6i - 4j + 6k, в = 9i - 6j + 9k, с = i - 8k;
а) 2а, -4в, 3с; б) –9с, 3в; в) -5с, 3а; г) а, в; д) 3а, -4в, -9с.
5.11. а = 5i - 3j + 4k, в = 2i - 4j - 2k, с = 3i + 5j - 7k;
а) а, -4в, 2с; б) 4с, -2в; в) 6с, -3а; г) с, в; д) а, -2в, 6с.
5.12. а = -4i + 3j - 7k, в = 4i + 6j - 2k, с = 6i + 9j - 3k;
а) -2а, в, -2с; б) 7с, 4в; в) –3в, 5а; г) с, в; д) -2а, 4в, 7с.
5.13. а = -5i + 2j - 2k, в = 7i - 5k, с = 2i + 3j - 2k;
а) 2а, 4в, -5с; б) 11с, -3в; в) –6с, 8а; г) с, а; д) 2а, 4в, -5с.
5.14. а = -4i - 6j + 2k, в = 2i + 3j - k, с = -i + 5j - 3k;
а) 5а, 7в, 2с; б) 11а, -4в; в) –7с, 3а; г) в, а; д) 3а, 7в, -2с.
5.15. а = -4i + 2j - 3k, в = - 3j +5k, с = 6i + 6j - 4k;
а) 5а, -в, 3с; б) -7а, 4с; в) 9в, 3а; г) с, а; д) 3а, -9в, 4с.
5.16. а = -3i + 8j, в = 2i + 3j - 2k, с = 8i + 12j - 8k;
а) 4а, -6в, 5с; б) -7а, 9с; в) 3в, -8с; г) с, в; д) 4а, -6в, 9с.
5.17. а = 2i - 4j - 2k, в = -9i + 2k, с = 3i + 5j - 7k;
а) 7а, 5в, -с; б) 5а, 4в; в) 3в, -8с; г) с, а; д) 7а, 5в, -с.
5.18. а = 9i - 3j + k, в = 3i - 15j + 21k, с = i - 5j + 7k;
а) 2а, -7в, 3с; б) -6а, 4с; в) 5в, 7а; г) с, в; д) 2а, -7в, 4с.
5.19. а = -2i + 4j - 3k, в = 5i + j - 2k, с = 7i + 4j - k;
а) а, -6в, 2с; б) –8в, 2с; в) 7с, -9а; г) а, в; д) а, -6в, 5с.
5.20. а = -9i + 4j - 5k, в = i - 2j + 4k, с = -5i + 10j - 20k;
а) -2а, 7в, 5с; б) –6в, 7с; в) 4с, 9а; г) с, в; д) -2а, 7в, 4с.
5.21. а = 2i - 7j + 5k, в = -i + 2j - 6k, с = 3i + 2j - 4k;
а) -3а, 6в, -с; б) 5в, 3с; в) –4в, 7а; г) с, в; д) 7а, -4в, 3с.
5.22. а = 7i - 4j - 5k, в = i - 11j + 3k, с = 5i + 5j + 3k;
а) 3а, -7в, 2с; б) 2в, 6с; в) –4а, -5с; г) с, а; д) -4а, 2в, 6с.
5.23. а = 4i - 6j - 2k, в = -2i + 3j + k, с = 3i - 5j + 7k;
а) 6а, 3в, 8с; б) -7в, 6а; в) 4с, -5а; г) в, а; д) -5а, 3в, 4с.
5.24. а = 3i - j + 2k, в = -i + 5j - 4k, с = 6i - 2j + 4k;
а) 4а, -7в, -2с; б) –4с, 6а; в) 5в, -2а; г) с, а; д) 6а, -7в, -2с.
5.25. а = -3i - j - 5k, в = 2i - 4j + 8k, с = 3i + 7j - k;
а) 2а, -в, 3с; б) 4с, -9а; в) 5в, -6с; г) с, в; д) 2а, 5в, -6с.