Главная | Обратная связь

Есепті тапсырыс бойынша шешу 2 страница

 

 

1. Сызықтық модельдер және әдістер

1.1 Оңтайлы шешім деген не, оңтайлау

есептерінің жіктелу принциптері

 

Шешiм қабылдау адам баласының барлық iс-әрекеттерiнде үлкен орын алады. Шешiм қабылдауға арналған есептердi қою үшiн екi жағдай орындалуы мiндеттi:

– шешiмдi қайдан, қалай iздеу керек;

– тек бiр мақсат көзделінген шешімде бірақ нұсқа таңдалы-нады.

Егер шешiм қабылдауды қажет ететін жағдайда шешімнің кем дегенде екі нұсқасы болмаса, онда шешiм таңдаудың қажетi жоқ. Демек, егер кәсiпорнына қандай өнiм және қанша өндiруi белгiлi болса, онда оған жоспар құрудың қажетi болмайды.

Шешiм таңдаудың екi принципi белгiлi: жiгерлi және крите-риялды.

Шешім қабылдау есебі реттелмеген, математикалық моделі құрылмаған жағдайда, қалған басқа кез келген уақытта жиi қолда-нылатын, жалғыз мүмкiн бола алатын шешiм, ол жiгерлi таңдаудеп аталады.

Бір критерия (грекше kriterion – бір шешімге келу үшін амал, өлшем, баға) арқылы барлық мүмкiн бола алатын нұсқаларды салыстырып, қабылданатын шешiм, критериялық таңдауделінеді. Осы қабылданған критерия бойынша ең ұтымды нұсқа, оңтайлы (орысша оптимально, латынша optimus) делiнедi, ал осындай есеп-тер – оңтайлау немесе сөйлемнің ыңғайына байланысты оңтай-ластыру есептерi деп аталады.

Шешiм барлық жағдайда, барлық мағынада оңтайлы болуы мүмкiн емес, ол қабылданған критерия бойынша табылған тек бiр жалғыз мағынада ғана оңтайлы.

Оңтайлау (оңтайластыру) критериясы – мақсат функциясы немесе мақсат функция немесе функционал деп аталады.

Сонымен шешiмi мақсат функцияның максимальды немесе минимальды мәнiн iздейтiн, кез келген есептi оңтайлау немесе оңтайластыру есебi деп атайды.

Басқаруда шешім қабылдау есептерiнде көбiнесе, өндіріс жағдайы шектеулі, яғни айнымалыларға қойылған шектеулер белгi-лi жағдайда мақсат функцияның экстремальды мәнiн iздеу шарты-мен байланыстырылады.

Әртүрлi оңтайластыру есептерін шығарғанда мақсат функция ретiнде шығарылатын өнiмнiң мөлшерi немесе бағасы, өндiрiс шығыны, барлық пайда, табыс және т.б. қабылданады. Шектеулер ретiнде жалпы жағдайда қорлар (ресурстар): адам еңбектерi, материалдық немесе ақшалай шығындар және т.б. алынады.

Қазіргі кезде сыртқы батыс мемлекеттерінде өндірісті басқа-руда ең көп таралған және әртүрлі атпен: шешім қабылдаудағы математикалық әдістер; әрекеттерді зерттеу; экономикалық-математикалық әдістер; экономикалық кибернетиканың әдістері; оңтайлы басқару әдістері; шешім қабылдау теориясы және т.б. аталып жүрген математикалық әдістер мен модельдер барлық сауатты мамандарға жақсы белгілі.

ХХ ғасырда кеңестер одағында, экстремальды математи-калық есептердi және олардың шығару әдiстерiн оқытатын мате-матикалық пән «Математикалық программалау» курсы деп атал-ды. Қазақ тілінде осы атпен бірнеше оқу құралдары [15, 16 және т.б.] жарыққа шықты. Экономикалық және математикалық ғылыми пәндер кешенін 60-шы жылдары кеңес одағының академигі В.С. Немчинов «Экономикалық-математикалық әдістер» (ЭММ) деп атауды ұсынды. Өндірістік (оның ішінде экономикалық) есептерді шығаруда пайдаланылатын қолданбалы математикалық әдістердің жиынтығы «Әрекеттерді зерттеу» деп аталды. Осы жерде қысқаша тарихи мәліметтерге көп тоқталмай, бір мағыналы әртүр-лі сөздіктерді құрастыру арқылы қарастырылып отырған мәселе бойынша орыс тілінде осы күнге дейін неше түрлі атпен біраз әдебиеттер жарыққа шығып жатқанын атап өтейік.

Жалпы жағдайда оңтайластыру есептерінің математикалық қойылуы мына жағдайда: g_i(x₁, x₂,…x_n) £ b_i, (i = 1,…m) мақсат функ-цияның f(x₁, x₂,…x_n) ең үлкен немесе ең кiшi мәнiн анықтаумен шектеледі. Мұндағы g_i және f – берiлген функциялар; x_j(j=1,…n) – мәндерi iзделiнiп отырған айнымалылар; b_i (i=1,…m) – қорлар мөлшері.

Бiрiншiден математикалық әдiстерді сызықтық және сызықты емес программалау есептерiн шешетін әдiстерге бөледi.

 

 

Егер барлық g_i және f – функциялары сызықты, немесе олардың айнымалыларының туындылары жоқ болса, онда мұндай есептердi сызықтық программалау (СП) есептерi дейдi.

Егер осы функциялардың кем дегенде бiреуi сызықты емес болса немесе айнымалыларының туындысы болса, онда мұндай есептер сызықты емес программалау (СЕП) есептерi делiнедi.

Шешу нәтижесiнде берiлген ойыс тұйықталған көпшiлiкте, ойыс функцияның минимумы (немесе дөңес функцияның максиму-мы) анықталатын ойыс программалау (ОП)есептерi сызықты емес программалау есептерiнiң iшiндегi ең көп таралғаны болып есептелiнедi.

Ойыс программалау есептерi iшiндегi терең құрастырыл-ғаны квадраттық программалау (КП)есептерi.Мұндай есептерде iзделiнiп отырған айнымалылар шектеулердi немесе теңдiктi қана-ғаттандырған жағдайда квадратты функцияның максимальды (ми-нимальды) мәнi iзделiнедi.

Жалпы экономикалық-математикалық әдiстер: сызықтық, сызықты емес, бүтiн санды, бөлшек сызықты және параметрлi программалау есептерi, сонымен қатар динамикалық және стохас-тикалық программалау есептерi болып бөлінеді.

Бүтiнсанды программалау (БП)есептерiндеiзделiнiп отыр-ған айнымалылар тек бүтiн мән қабылдайды.

Параметрлi программалау (ПП)есептерiнде мақсат функ-цияның мәнi немесе айнымалылардың өзгеру мәндерiнiң мүмкiн бола алатын аймағын анықтайтын функция немесе екi функцияда басқа бiр параметрге байланысты болуы мүмкiн.

Бөлшександы программалау (БСП)есептерiнде айнымалы-лардың өзгеру мәндерiнiң мүмкiн бола алатын аймағын анықтайт-ын функция сызықты, ал мақсат функция екi сызықты функциялар қатысынан тұрады.

Динамикалық программалау (ДП)есептерi күрделі есептер қатарына жатады. Онда iзделiнiп отырған айнымалылардың мәнiн іздеуде, жұмыс, күрделi есептеулер жүргізілетін көп кезеңдерден тұратын әрекеттерден құралады.

Егер мақсат функция немесе айнымалылардың өзгеру мәнде-рiнiң мүмкiн бола алатын аймағын анықтайтын функция кездейсоқ шамалардан тұратын болса, онда мұндай есептердi стохастикалық программалау (СТП) есептерiне жатқызады.

Стандартталған программалар пакеттерiн және экономика-лық-математикалық модельдер сыныптарының қолдануы бойынша басқару шешімдерін қабылдауда оңтайластыру есептерi әртүрлi болуы мүмкін. Өндірісті басқару үшін орындалатын оңтайластыру есептерi: басқару функциясы; оңтайластыру есептерiнiң құрамы және экономикалық-математикалық модельдер белгiлерi бойынша 1.1-кестеде келтірілген ретпен жіктелінеді.

 

1.1-кесте. Оңтайластыру есептерiнiң жiктелуi

Басқару функциясы	Оңтайластыру есептерi	ЭММ-дiң сынып-тары
Өндiрiсте техникалық және ұйымдастыру дайындықтарын жасау	– мүлiктердiң құрамын модельдеу; – маркалардың, шихталардың және қоспалардың құрамын оңтайластыру; – жазық және әртүрлi мүлiктер жасау-ға арналған материалдарды тиiмдi пiшудi модельдеу; – қорларды тиiмдi бөлiп тарату және әртүрлi жұмыс кешендерiнiң торлық модельдерi; – әртүрлi құрал-жабдықтар жасайтын кәсiпорындарына оңтайлы жоспар құру модельдерi; – техникалық тетiктердi және технологиялық оңтайластыру модельдерi;	Графиктер теориясы. Бүтiнсанды (дискреттi) программалау (БП). Сызықтық программалау (СП). Кейiптiк модельдеу. Динамикалық және сызықты емес программалау.
Техникалық-экономикалық жоспарлау	– бос жоспар құру және кәсiпорын-ның даму көрсеткiштерiн жобалау; – қаржы қоры портфелiн және өндiрiс жоспарын оңтайластыру; – жоспарлау кезеңдерi бойынша өндiрiс бағдарламасын оңтайластыру.	Баланстау («Шы-ғын-шығару») моделi. Корреляция-лық-регрессиялық талдау. Дамыу үстемдiгiн экстре-поляциялау. СП.
Негiзгi өндiрiс-тi жедел басқа-ру	– күндiзбектiк-жоспарлау, нормативтiк оңтайластыру; – күндiзбектiк есептер; – стандартты-жоспарларды оңтайлас-тыру; – қысқа мерзiмдiк өндiрiстiк жоспарларды оңтайластыру.	Сызықты емес программалау. Кейiптiк модельдеу. СП және БП.

Алғашқы мәлiметтерге (деректерге) байланысты басқару есептерiнiң математикалық өрнектелуi үш типке бөлiнедi: детер-миниялдықтар, ықтималдылықтар және анықталмаған жағдайдағы есептер. Осындай шешім қабылдауға (ШҚ) арналған модельдердің мындай ерекше белгілерін: алғашқы мәлiметтерi, iзделiнетiн айнымалылары, байланыстары, есептiң мақсатын және шектеулерiн өрнектейтiндерді (бейнелейтiндер), бiр жүйеге келтiріп, оларды 1.1-суретте көрсетілген түрлерге жіктеуге болады.

ШҚ модельдердің жіктелуі

 

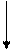
1.1-сурет. Модельдерді айнымалылар қасиеттері бойынша жiктеу

 

Бастапқы мәлiметтерi белгiлi бiр шамалармен берiлген есеп-тердi детерминиялдыдеп атайды.

Детерминиялық есептер, қолданылатын параметрлерінiң ша-малары, құрамы, байланыстары және шектеулерi толық анықтал-ған, айқын жағдайда құрылады, яғни олар математикалық көзқа-раста бiр мәндi және нақтылы шешiм алуға ыңғайлы болады.

Детерминиялық есептерде, А – стратегиялық iс - әрекетте «а» – нәтижесiне әкелетiндiгi, ал В – стратегиялық iс-әрекетте «в» – нәтижесiне әкелетiндiгi әрқашанда белгiлi. Тек, қандай нәтиже көп пайдалы екендiгiн анықтау қажет, яғни қандай стратегиялық iс-әрекет тиiмдi.

Халық шаруашылығы модельдерінде g_i және f – функция-лардың қасиеттерiне байланысты экономикалық-математикалық әдiстер әртүрлi есептер сыныбына бөлiнедi, олар әртүрлi әдiстер-мен арнайы программалар пакеттерін қолдану арқылы шешіледі (1.2-кесте).

Егер алғашқы мәлiметтер мәні кездейсоқ факторларға байла-нысты өзгеріп отыратын болса, онда мұндай есептерді кездейсоқ мәнді есептердеп атайды. Мысалға, бар қорлардың шамасы, зат-тардың дер кезiнде жеткiзiлуiне, құрал-жабдықтың өнiмдiлiгiне, олардың техникалық қалпына және т.б.с.с. жағдайға байланысты болған жағдайда нәтижелік көрсеткіш кездейсоқ мән қабылдайды.

1.2- кесте. Оңтайластыру есептерiнiң сыныптары

Алғашқы мәлiметтер	Айнымалылар	Байланыстар	Есептер
Детерминиялды	Үздiктілер	Сызықтылар	СП
Бүтiнсандылар (Дискреттiлер)	Сызықтылар	БП
Үздiктілер және бүтiнсандылар	Сызықтылар	Жарым-жартылай бүтінсанды прогр.
Үздіктілер	Сыз.еместер	СЕП
Кездейсоқтар	Үздiктілер	Сызықтылар Сыз. еместер	СТП және ДП

 

Сөйтіп, мұндай есептерді ықтималдық немесе стохастикалық есептер деп те атайды, өздерiнiң қойылуында кездейсоқ шамалар-дан тұратын параметрлер қарастырылады. Осы параметрлердің мүмкiн бола алатын шамаларына қандай ықтималдықпен жетуге болатыны берiледi. Мұндай есептер, алғашқы жағдай айқын емес кезде тәуекелдік (орысша – риск) есептерi деп атайды және олар-дың шешiлу нәтижесiнiң ықтималдық бағалары вектор түрiнде қалыптасады.

Осы жерде детерминиялды есептер нәтижесiн, ықтималдығы бiрге тең тәуеклдік есебi шешiмiнiң ең шеткi шегi алынатын нұсқа-сы деп қарастыруға болатынын атап өтейік.

Ықтималдылық баға екi типте болу мүмкiн: объективтi және субъективтi. Объективтi ықтималдық баға, керектi белгілер саны-ның барлық тексерiлген белгілер санына қатынасы арқылы анықта-лынады.

Мүмкiн болатын келешектегi жағдайдың алдынала ықтимал-дық бағасы немесе олардың параметрлерiн сипатайтын мәліметтер белгiсiз жағдайда, алғы шарты анықталмаған есеп қалыптасады. Мұндай есептерді шешу барысында басқару стратегиялар ішінен тиімдісін анықтайтын бағаны дәйектеу үшін, ерекше қатынастар және есептi шешу жолдары қарастырылады. Оларды максимакс немесе минимакс немесе максимин бағалары деп атайды. Есепте максимин баға қарастырылған кезде максимальды пайдалы нәтиже-ге ешқандай сырттай ештеңенiң әсерiнсiз жеткiзетiн стратегиялық iс-әрекет жасауға көңіл аударылады. Минимакс баға қарастырылса мүмкiндігiнше аз шығынмен максимальды пайдаға жеткiзетiн стра-тегиялық iс-әрекет жасауға мән берiледi.

Оңтайластыру модельдерін шешудегі негізгі кезеңдер:

– мағыналы есепті қою;

– есеп туралы барлық деректерді жинау, реттеу (формалдау);

– математикалық модельді құру;

– компьютерге сандық-кестелік модельді енгізу және шешу;

– есептің шешім нәтижесін талдау;

– есептің шешім нәтижесін графикпен бейнелеу;

– шешім нәтижесі бойынша оңтайлы шешім қабылдау.

Алдыңғы үш кезеңдер туралы терең мағыналы түсініктер математикалық әдістер мен модельдер пәндерінде [1, 2, 12, 15, 16] жан-жақты баяндалған. Сондықтан оларға тоқталмаймыз. Бұл жер-де біздерге қызықтысы соңғы төрт кезең.

1. Компьютерге сандық-кестелік модельді енгізу және шешу – бұл, сөзсіз, осы кітапта әрбір оңтайластыру есептер сыны-бы үшін жан-жақты қарастырылған, ең негізгі жауапты сұрақ. Сандық-кестелік модельді Excel-дің жұмыс бетіне құру тәсілдері келесі бөлімдерде қарастырылады, ал оны шешу әдістерін анықтау жауапты мәселе және ол туралы да кітапта керекті ақпараттар беріледі.

2. Есептің шешім нәтижесін талдау – оңтайлы шешімдер қабылдауға керекті ең маңызды аспап. Ол туралы толық мәліметті – келесі бөлімдерде қарастырамыз.

3. Есептің шешім нәтижесін графикпен бейнелеу – шешім қабылдау үшін қажетті ақпараттарды көрнекі бейнелеуге қуатты фактор. Бұл кезең, келесі бөлімдерде толық баяндалынады.

4. Шешім нәтижесі бойынша оңтайлы шешім қабылдау – жұмыстың соңғы кезеңі. Шешім қабылдайтын компьютер емес, Excel-де емес, қабылданған шешім нәтижесіне жауап беретін, есепті қойып, компьютерде шешуші адам.

Осы жерде оңтайлы шешім – тек Excel мен орындалған іздеу жұмысының нәтижесінде алынған мәндер емес, ол іздеу көмегі-мен алынған шешім нәтижесімен және жүргізілген талдау арқылы анықталған мәндерді бірге жан-жақты бағалау нәтижесі.

Сонымен, кітапта келесі бөлімдерде қарастырылатын, әртүр-лі есептерді шешу арқылы бірнеше рет бейнелеп көрсетілетін, оң-тайлы шешімдер қабылдаудың негізгі кезеңдері осындай.

Есептің математикалық моделі құрылғаннан кейін келесі ке-зекте оны шешу әдісін анықтаймыз. Ол үшін оңтайластыру модель-дерін шешу әдістері бойынша жіктеу принциптерін білу қажет. 1.3-кестеде оңтайластыру модельдерін жіктеу принциптері берілген.

1.3-кесте. Оңтайластыру модельдерінің шешу әдістері бойынша жіктелуі

Айнымалылар	Мақсат функциясы	Шектеулер функциялары	Модельдің типі	Шешу әдісі
Үздіксіз	Сызықты	Сызықты	Сызықты	Симплекс әдісі
Кемінде бір айнымалы бүтін сан	Сызықты	Сызықты	Жарым-жар-тылай немесе толық бүтін- санды сызық-ты	Бұтақ және шекара әдісі
Үздіксіз	Сызықты	Жоқ	Шартсыз сызықсыз	Градиенттік әдістер
Үздіксіз	Шектеулер сызықсыз, мақсат функция сызықты немесе керісінше	Шартты сызықсыз	Градиенттік әдістер

 

Айнымалылардың үздікті немесе бүтін санды болуы туралы жай қарапайым математикалық пәндерден мектеп қабырғасында-ақ түсінік алғанбыз. Сондықтан оларға тоқталудың қажеті болмас. Дегенмен де, бүтін санды айнымалылармен қатар екілік айнымалы болатынын және олар 0 мен 1 мәнді екенін ескертеміз. Олар туралы кітапта тиісті тақырыптарда кеңінен тоқталамыз және екілік айны-малылар шешім қабылдау үшін құрылған математикалық модель-дерде жиі қолданылатынын атап өтейік.

Сызықты емес оңтайластыру модельдерінде екі жағдай – мо-дельдің құрамында шектеулер жоқ (шартсыз оңтайластыру мо-делі), модельдің құрамында шектеу бар (шартты оңтайластыру моделі) қарастырылады. Шешім қабылдау жағдайларында бірінші түрдегі модельдер көп кездеспейді, себебі өмірде нақтылы жағдай-да әрқашанда қойылған мақсатқа жетуге шектеулер түрінде бірдеңе кедергі жасайды. Шартсыз модельдерде мақсат функцияның сы-зықты емес болуы қажетті, себебі мақсат функция минимумге немесе максимумге ізделінсе және есепте шектеулер жоқ болса, онда мұндай жағдай айнымалылардың шексіз мәндері болуына әкеледі.

1.3-кестеде келтірілген модельдерді шешу әдістері туралы бір-екі ауыз сөздер. Саспаңыз, кітапта қарастырып отырған әдістер туралы толық теориялық мәліметтер келтірілген жоқ. Оларды осы жерде еске алып отырған себебіміз, сіздер әрбір модельдерді шеш-кен кезде оларда өздеріне тән әдіс қолданатынын және соған бай-ланысты әртүрлі нәтижелер алынатынын білгендеріңіз жөн. Кес-теде келтірілген модельдерден басқа да кез келген типтегі модель-дерді шешуге арналған көптеген әдістер бар екенін, симплекс әдісінен басқа да әдістермен сызықтық модельдерді шешуге бола-тынын білесіздер. Кестеде келтірілген әдістер Поиск решения құралының құрамында қарастырылған. Оларды біз MS Excel-де модельдерді шешуде қолданамыз. Модельдерді шешу үшін қолда-нылатын әдіске байланысты Поиск решения құралының пара-метрлері түзетіледі және алынған шешімнің нәтижелерін талдау үшін әртүрлі мүмкіншіліктер пайда болады. Сондықтан қарасты-рылып отырған модельді қандай әдіспен шешетініңізді, сіз анық түсінсеңіз, нақтылы нәтижеге жететініңіз сөзсіз.

 

 

1.2 Модель және модельдеу туралы негізгі түсінік

Нақтылы объектілерді оқып, зерттеу нәтижесінде олардың әртүрлі қасиеттері және бір-бірімен арақатынастары жөнінде адам- да бір пікір қалыптасады. Осы зерттеу объекті туралы қалыптасқан көзқарасы бойынша адам оны суреттейді, ол үшін арнайы суреттеу тілі қолданылады. Суреттеу тілі сөзбен (вербальдық модельдер), математикалық формулалар, суреттер, сызбалар, графиктер, макет-тер және т.б. болуы мүмкін. Осылардың барлығын тұжырымдап модель деп, ал модельдерді тұрғызып, олардың шешімін іздеу жұмыстарын модельдеу деп атайтыны бәрімізге белгілі [1,2,3 және т.б.].

Модельдеу – нақтылы өмірдегі құбылыстарды және үрдістер-ді оқып, зерделейтін әмбебап тәсіл. Қазіргі ақпараттық техноло-гиялар дамыған заманда, бірден тура зерттеуге жатпайтын объекті-лерді оқып, зерделу үшін оны модельдеу ерекше маңызды. Мо-дельдеу шешім қабылдау жұмыстарында айрықша өзекті мәселеге айналды. Қазіргі кезде математикалық әдістермен модельдерді кеңінен пайдалану арқылы «Шешім қабылдау» теориясы дамыды және қалыптасты.

Математикалық әдістер және модельдер бірнеше пәндер жиынтығы екені жоғарыда айтылды. Солардың ішінен аграрлық жүйеде шешім қабылдауда көп қолданылатыны сызықтық про-граммалау әдістері (СП).

СП модельдері мақсат функциядан, шектеулер жүйелерінен және айнымалылардың теріс болмау шартынан тұратыны белгілі. Дегенменде, СП модельдерінің қысқаша математикалық формула-лары мен ондағы көрсеткіштерді тағыда еске түсірейік.

Экстремальды (яғни максимальды немесе минимальды) мәні ізелінетін математикалық өрнек мақсат функция деп аталады, мысалға,

Z =

мұндағы c_j – мақсат функция коэффициенті.

Айнымалыларды теңдік және теңсіздік түрінде байланыс-тыратын математикалық өрнекті шектеу деп атайды. Барлық шектеулер есептің шектеулер жүйесін құрайды.

Шектеулер үш түрлі болуы мүмкін: теңдік (=), көп емес немесе тең типті теңсіздік түрінде (≤), кем емес немесе тең типті теңсіздік түрінде (≥). Мысалға,

 

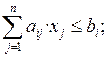
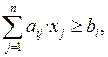
мұндағы i = 1, 2, … , m; a_ij – айнымалылар коэффициенттері (мұндағы индекс i – шектеулер нөмірі, индекс j – айнымалылар нөмірі), b_i – бос мүшелер (шектеулердің оң жағы) индекс i – шектеулер нөмірі.

 

Айнымалылардың теріс болмау шарты мына түрде жазы-лады:

x_j ≥ 0, j = 1, 2, …, n немесе

СП модельдерінің жалпы стандартты жазылу түрі:

– мақсат функцияның максимальды мәні ізделінсе

 

Z = (1.1)

 

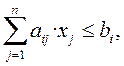i = 1,…, m немесе 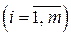, (1.2)

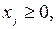j = 1, …, n немесе (1.3)

– мақсат функцияның минимальды мәні ізделінсе

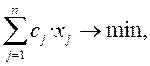Z = (1.4)

i = 1, …, m немесе 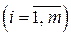(1.5)

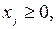j = 1,…,n немесе (1.6)