Главная | Обратная связь

Есепті тапсырыс бойынша шешу 5 страница

 

1.5.2 Жүйеде шектеулер бірікпеген немесе мақсат фукция

шектелмеген жағдайларда жасалынатын әрекеттер

Жоғарғы тақырыпта қарастырылып отырған есептердің шешімі әрқашан да бірден табыла бермейтінін атап өттік. Мұндай жағдай көбінесе қорларды өндірілетін өнім бойынша бөлгенде, есептің шарты жүйеде бірікпеген немесе мақсат функция шектел-меген жағдайларда пайда болады. Бірінші кезекте жүйеде шектеулердің сәйкестендірілмеген жағдайында қандай әрекеттер жасау керектігін қарастырайық. Есепте, оңтайлы шешім бойынша шаруашылыққа 1-ші (х₁ = 250 ө.б.) және 3-ші (х₃ = 535,71 ө.б.) өнімдерді өндірумен айналысу пайдалы делінді. Осы жағдайда еңбек шығыны және қаржы толығымен қолданылатынын байқадық (1.9-сурет). Жүйеде шектеулердің сәйкестендірілмеген жағдайын жасанды тудыру үшін, оңтайлау шешімін сақтап, бірақ 2-ші өнімді 100 ө.б. кем емес өндіру керек делік. Бұл жалған шарт, оқу мақсаты үшін қарастырылып отыр. Сөзсіз, ол қорлардың жетіспейтіндігіне әкеледі де, шектеулер бірікпеген деп Поиск решения хабарлайды (1.10-сурет).

Excel-де мұндай шектеулердің бірікпеген жағдайынан қалай өтуге болатынын қарастырайық. Ол үшін есептің математикалық моделіне көңіл аударайық. Шектеулердің бірікпеген себебін білу үшін керекті қосымша қорды u_i модельге енгізейік, яғни модельді мына түрде жазамыз:

Z= 135х₁+125х₂ + 150х₃ +130х₄ → max

мына жағдайда:

1,9х₁+ 1,77х₂ + 2,1х₃ + 2 х₄ = 1600 + u₁

9,5х₁+ 8х₂ + 10,5х₃ + 8,9х₄ = 9000 + u₂

10х₁+ 7,5х₂ + 14х₃ + 7,3 х₄ = 10000 + u₃

; u_i ≥ 0, i =1,2,3.

Есепті осылай қою, керекті қосымша қорлардың u₁, u₂, u₃ минимальды мәнін анықтауға мүмкіндік береді. Сондықтан беріл-ген жүйені мына түрде жазайық:

F= u₁+ u₂ + u₃ → min

Z= 135х₁+125х₂ + 150х₃ +130х₄

1,9х₁+ 1,77х₂ + 2,1х₃ + 2 х₄ – u₁= 1600

9,5х₁+ 8х₂ + 10,5х₃ + 8,9х₄ – u₂ = 9000

10х₁+ 7,5х₂ + 14х₃ + 7,3 х₄ – u₃ = 10000

; u_i ≥ 0, i =1,2,3.

Осыдан кейін 1.3-суреттегі кестелік модельге біраз өзгерістер енгіземіз. Енгізілген өзгерістер 1.13-суретте көрсетілген. Бірінші-ден, жаңа айнымалылар белгілері F3:H3 аралығындағы бағаналарға жазылғанда, ал олардың мәндері үшін F4:H4 аралығын тағайын-далған. Екіншіден, шектеулерге осы жаңа айнымалылардың (u₁, u₂, u₃) бағаналарына олардың коэффициентері (-1) жазылады.

Жаңа мақсат функция үшін 5-ші жолда жаңа айнымалы-лардың (u₁, u₂, u₃) бағаналарына олардың коэффициенттері (1) жазылады да, ал I5-ұяда оның мәні анықталынады. Ескі мақсат функция формуласы өзгеріссіз қалады (1.13-сурет).

 

1.13-сурет

 

Сервис.. Поиск решения..Мақсат функцияны (I5-ұя) мини-мальды мәнін іздеуге орналастырамыз. Изменяя ячейки терезесіне B4:H4. Осыдан кейін шектеулердің шарттарын енгіземіз: B4 =250; C4 = 100; D4 = 536 және E4:H4>=0. Есеп Выполнить бұйрығы бойынша шешуге жіберіледі. Есептің шешімі 1.13-суретте берілген. Суреттен көріп отырмыз ізделініп отырған қосымша қорлардың мөлшері u₁ = 178ө.б. , u₃ = 754 ө.б. және u₂ = 0. Сөйтіп, өнімдер-ді берілген көлемде өндіру үшін шаруашылықтағы қорлар мөлшері болу керек:

еңбек қоры 1600 + 178 = 1778 ө.б.;

шикізат 9000 + 0 = 9000 ө.б.;

қаржы 10000 + 754 = 10754 ө.б.

Осы жағдайда 126650 а.б. пайда алынады.

Шектеулер жүйесінде теңсіздіктер сәйкестендірілмеген жағ-дайда мұндай әдісті қолдану өте құнды. Егер нақтылы шаруа-шылықтың жағдайында көрсетілген деңгейге дейін қорларды көбейтуге мүмкіндік жоқ болса, онда алғашқы есептің қойылуы сияқты, ізделініп отырған айнымалыларға теріс болмау шартын жазамыз да (х_i≥0), есепті қайта шығарамыз. Онда шаруашылықтағы қорлардың мүмкіндіктеріне сәйкес жаңа шешім алынады. Сөзсіз, пайда азайады.

Мақсат функцияның шектелмеуі туралы Поиск решения-дан мынадай хабарлама алынады: Значения целевой ячейки не сходятся.

Мақсат функцияның шектелмеуі екі жағдайда байқалады. Мақсат функцияның шексіз үлкеюуіне немесе кемуіне жібермейтін есептің шешімдері мүмкін бола алатын аймақ шектелмеген болса, онда есеп шешілмейді. Сондықтан:

· мақсат функция максимумге ізделінсе есептің шешімдері мүмкін бола алатын аймақ жоғарыдан шектелуге тиіс;

· мақсат функция минимумге ізделінсе есептің шешімдері мүмкін бола алатын аймақ төменнен шектелуге тиіс.

Осы ережелерді ұққаннан кейін, мақсат функцияның шектел-меуін жеңіл түзетуге болады. Есептің шартын және шектеу белгі-лерін тексеріп, мүмкіндігінше түзетулер енгізіледі. Қосымша шектеу енгізу мүмкіндіктері қарастырылады.

 

1.5.3 Оңтайлы шешімді талдау

Поиск решениясызықтық модель есебін шешу нәтижесінде үш есеп (отчет) беретіні туралы жоғарыда айтылды.

Нәтиже бойынша есеп (1.14-сурет). Есеп үш кестеден тұрады. Бірінші кестеде мақсат функция туралы мәліметтер, екінші кестеде есепті шешу нәтижесінде алынған, іздеп отырған айнымалылардың мәндері және үшінші кестеде шектеулер үшін және шекаралық шарттар үшін оңтайлы шешімнің нәтижесі алынады (1.14-сурет).

Қандай шектеулер байланысты (связанное) және қандай шектеулер байланыссыз (не связан.)екенін анық көрсетуіне байланысты, нәтиже бойынша есеп сезімталдықты талдауда пайдалы. Бұл мәліметтер есепте, Шектеулер кестесінде Статус бағанасында берілген. Сол кестенің Разница бағанасында шектеулердің оң және сол жақ бөліктерінің айрымдарының мәні көрсетілген. Көріп отырмыз, егер қор толық қолданылса шектеу байланысты, ал керісінше жағдайда байланыссыз делінеді.

Егер ізделініп отырған айнымалылар мәндерінің төменгі және жоғарғы өзгеру аралығы белгілі болса, онда нәтиже есебінің үшінші кестесінде қорлардан кейін жалғастырылып, осы айныма-лылардың шекаралық шарттары орындалуы туралы (жоғарыда аталған бағаналарда) есеп беріледі. Біздің мысалда, мұндай шарт қарастырылмаған.

1.14-сурет

 

Сезімталдықты талдауда орнықтылық есебі басқа есептерге қарағанда мәндірек. Орнықтылық есебі екі кестеден тұрады (1.15-сурет). Бірінші «Белгісіздер ұясы» кестесінде мынадай мәліметтер беріледі:

- есептің шешім нәтижесі;

- нормированная стоимость (немесе v_і–қосымша қосалқы айнымалы);Қосымша қосалқы айнымалылардың мәнісі неде? Қосымша қосалқы айнымалылар (нормированная стоимость) деп қосалқы есепті теңдікке түрлендіргендегі қосымша v_і-айныма-лыларды атайды. Негізгі айнымалылар (х₁, х₂, х₃, х₄) ішінен оңтайлы шешімге енгендеріне (біздің мысалда, х₁=250 және х₃=536) сәйкес қосымша қосалқы айнымалылар (v₁=0 және v₃= 0), ал енбегендеріне (біздің мысалда, х₂=0 және х₄=0) сәйкес қосымша қосалқы айныма-лылар (v₂ = - 0,2767857 және v₄ = -11,241). Егер осы оңтайлы шешімге енбеген өнімдерді еріксіз оңтайлы шешімге ендірсек, онда олардың бір бірлігі енген жағдайда, қосымша қосалқы айныма-лылар теріс болса мақсат функция олардың шамаларына өседі, ал оң болған жағдайда керісінше кемиді.

Біздің мысалда,2-ші өнім бір бірліктей еріксіз өндірілсе мақсат функция: Z=114107,1+1·0,2767857=114107,3767857 а.б. және сәйкесінше 4-ші өнімде – Z= 114107,1 + 1· 11,241 = 114118,341 а.б., яғни қосымшалар (нормированная стоимость) шамасына өсті. Осы жерде мынадай сұрақ туады: қанша шекараға дейін бұл қортынды сенімді? Зейін қойсаңыз, жауапты келесі тұжырымдарда аласыз;

Допустимое увеличение және Допустимое уменьшение баға-наларындағы мәндер, айнымалылардың табылған мәндері өзгеріс-сіз қалған жағдайда, мақсат фукция коэффициенттері қандай аралықтарға дейін өзгеретінін көрсетеді.

 

1.15-сурет

 

Екіші кестеде шектеулер үшін бірінші кестедегі сияқты көрсеткіштер берілген:

– орлардың қолданылған шамасы;

–көлеңкелік құн (MS Excel-де аталуы), әдебиеттерде қосалқы бағалар у_і деп аталады. Егер оңтайлы шешімде i-қор толығымен қолданылмаса, оның шамасы өндірістегі басқа қорлар шамасымен балансталмаған, яғни артық мөлшерлі болса, онда сол i-қор шектеуінің қосымша айнымалысының мәні сол артық мөлшерге, ал осы шектеудің қосалқы бағасы (көлеңкелік құн) нөлге (у_і =0) тең болады. Біздің мысалда, шикізат қоры толығымен қолданылмады, қосымша айнымалы мәні 1000 тең, ал қосалқы баға (у₂=0). Еңбек және қаржы қорлары толығымен қолданылды, сондықтан олардың қосымша айнымалылары нөлге тең, ал қосалқы бағалары, сәйке-сінше: у₁=69,64 және у₃ = 0,26785. Сонымен қатар қосалқы бағалар мәні, қорлар шамасы бір бірлікке өзгергенде мақсат функция мәні қаншалықты өзгеретінін көрсетеді. Кестеден көріп отырмыз, шаруашылықта еңбек қоры өте құнды (у₁ = 69,64). Еңбек қоры бір бірлікке көбейсе: Z=114107,1 + 1·69,64=114176,74 немесе бір бірлікке азайса: Z=114107,1 – 1·69,64=114037,46. Қаржы қоры жөнінде осындай есептеулерді келтіруге болады. Бірақ, мақсат функция мәні айтарлықтай өзгеріске ұшырамайтынын қосалқы бағаның мәнінен-ақ байқауға болады. Осы жерде, қанша шекараға дейін мұндай есептеулер сенімді? – деген заңды сұрақ туылады. Зейін қойсаңыз, жауапты келесі тұжырымдарда аласыз;

– оңтайлы шешімге енген айнымалылар сол қалпында қалып және өздерінің оңтайлы мәндерін сақтайтын жағдайдағы қорлар-дың өсу және кему аралығы, яғни мысалда, еңбек қоры 200, шикізат шексіз және қаржы 666,67 бірлікке өсіп, сәйкесінше 100, 1000 және 1578,95 бірліктей азая алады.

Шекаралық бойынша есеп (1.16-сурет). Оңтайлы шешім құрамын сақтай отырып, оңтайлы шешімге енген өнім мөлшерін қанша аралыққа дейін өзгертуге болатыны туралы мәлімет осы есепте беріледі (суретті қараңыз):

– оңтайлы шешімдегі х_j шамалары;

– х_j шамаларының өзгеріс аралықтарының төменгі шегі.

 

1.16-сурет

 

Шекаралық есепте, берілген өнімді ең төменгі деңгейінде өндіргендегі мақсат функция мәні көрсетілген. Мысалға, 80357,14 мән былай алынған: Z = c₁x₁+ c₃x₃ = 35·0 + 50·535,71= 80357,14289.

Сол сияқты ең жоғарғы деңгейі бойынша: Z = c₁x₁ + c₃x₃ = =135·250 + 150·535,71 = 114107,1429.

Сонымен, есептерде қандай мәліметтер берілгенін баяндауды аяқтадық. Бірақ, бұл түсініктерден шешімді талдау толық бітпей-тінін тағы да ескертеміз. Тәжірибелік есептерді шешкенде толық талдау жасау барысында, бірнеше өндірістік сұрақтарға жауаптар алынады.

Қорлар –шамаларының және мақсаттық – коэффи-циенттерінің өзгеріс өсімі (кемуі) туралы талдау және шешім қабылдау жөніндегі әрекеттерге кеңірек тоқталайық.

Excel (1.15-сурет) есебіндегі бірінші кестеде Допустимое уменьшение деп аталатын бағанадағы с₁ – мақсаттық коэффи-циенттің төменгі өзгеру шегі 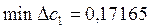және Допустимое увеличение деп аталатын бағанадағы оның жоғарғы өзгеру шегі . Енді осы өсімдерден с₁ шамаларының шеткі мәндеріне өтетін болсақ, онда:

Сонымен, с₁ мынадай өзгеру аралығында: ,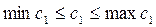

яғни 134,82835 ≤ c₁≤ 135,71485, x₁ өнімді 250 ө.б. шамасында өндіру бұрынғыша тиімді. Тек, бұл кезде мақсат функция мәні мына қатынаста өзгереді:

Z_min = Z – x₁ 114107,1 – 250·0,17165 = 114064,18,

Z_max = Z + x₁ 114107,1 + 250·0,71485 = 114285,81.

Тура осындай түрлендіруді басқа с₂, с₃ және с₄ жасасақ, онда

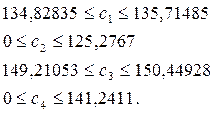
Мақсат функция коэффициенттері шамаларының осы көрсе-тілген шекараларында алғашқы шешімде анықталған өнімдер мөл-шерлері бұрынғы қалпында қала береді.

Қорлар өзгерісінің әсерін еңбек қоры мысалында қарасты-райық. Excel (1.15-сурет) есебіндегі екінші кестеде в₁ – еңбек қорының Допустимое уменьшение бағанада төменгі өзгеру шегі 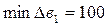және Допустимое увеличение бағанасында жоғарғы өзгеру шегі Келтірілген өсімдер бойынша в₁ шама-ларының шеткі мәндерін есептейік:

Сөйтіп, в₁ өзгеру аралығы: 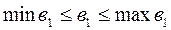, яғни 1500 ≤ ≤в₁≤ 1800.

Осындай в₂ және в₃ түрлендіруден кейін, қорлар шамалары-ның мынадай өзгеру шекарасы алынды:

Қорлар шамаларының табылған шекараларында оңтайлы шешім құрамы, яғни өндірілетін өнім түрлері өзгерусіз қалады. Бірақ, олардың оңтайлы мәндері өзгереді. Мысалға, оңтайлы шешімде алынған (x₁ және x₃), өндірілетін өнімдердің жаңа (х_1ж және х_3ж) мәндерін, сонымен қатар мақсат функция мәнін:

– еңбек қорының минимальды шектік мәнінде

х_1ж = x₁ – 2,5 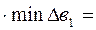250 – 2,5 · 100 = 0,0;

х_3ж = x₃ + 1,785 536 + 1,785 ·100 = 714,5;

Z_min = Z – y₁ 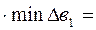114107,1 – 69,64∙100=107142,9 және

– еңбек қорының максимальды шектік мәнінде

х_1ж = x₁ + 2,5 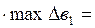250 + 2,5 · 200 = 750,0;

х_3ж = x₃ – 1,785 536 – 1,785 ·200 = 179,0,

Z_max = Z + y₁ 114107,1 + 69,64∙200=128035,7

анықтауға болады.

Осындай есептеулерді в₃ – қаржы қорына да жүргізейік.

– қаржы қорының минимальды шектік мәнінде

х_1ж = x₁ + 0,375 250 + 0,375 · 1578,95 = 842,1;

х_3ж = x₃ – 0,34 536 – 0,34 ·1578,95 = 0,0;

Z_min = Z – y₃ 114107,1 – 0,268∙1578,95=113684,2 және

– қаржы қорының максимальды шектік мәнінде

х_1ж = x₁ – 0,375 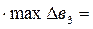250 – 0,375 · 666,67 = 0,0;

х_3ж = x₃ + 0,34 536 + 0,34 ·666,67 = 762,0;

Z_max = Z + y₃ 114107,1 + 0,268∙666,67=114285,7.

Осы жерде қаржы шамасы көбейген кезде пайданы макси-мальдау үшін x₁ өнімді өндіруді азайтып, керісінше x₃ өнімді өндіруді көбейту керектігін байқаймыз. Неге? Жауап. x₁ өнімнің бір бірлігіне кететін қаржы шығыны x₃ өнімге қарағанда 14 – 10 = 4 а.б. аз болғанымен, 3-ші өнімнің бір бірлігінен түсетін пайда 1-шіге қарағанда 150 – 135 = 15 а.б. артық (1.13-суретті қараңыз) және оның тиімділік әсері 1-шіге қарағанда 15/4=3,75 есе көп. Сондықтан қаржы көбейген кезде 3-ші өнім пайдалы және x₃ мөлшерін көбейту арқылы жалпы пайданы көбейтуге болатынын жоғарыда келтірген есептеулер көрсетіп тұр.

Математикалық модельдің көмегімен қаншама маңызды сұрақтарға жауап алуға болатынынын көрсету үшін, жоғарыдағы келтірілген мысалдардағы есептеулер жеткілікті деп ойлаймыз.

Көптеген әдебиеттерде соңғы симплекстік кестенің көмегі-мен, ешқандай да күрделі есептеулер жүргізбей-ақ осындай жауап-тар алынуы мүмкін делінеді. Бірақ, мұндай тұжырым, бүгінгі MS Excel мүмкіндігін ескерсек, біздің ойымызша онша дәйекті емес. Біріншіден, соңғы симплекс кестені алу үшін де қыруар есептеулер жүргізу керектігі әркімге белгілі. Одан ештеңе де ұту мүмкін емес. Екіншіден, соңғы кестеде келтірілетін, мына көрсеткіштерді: 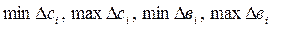анықтауға қажет, базистік айныма-лылар коэффициенттерінен құралатын матрицалардың кері матри-цасынан басқа, мәліметтердің барлығы да бізге белгілі. MS Excel көмегін қолданғанда бізге кері матрица қажет емес, өйткені аталған және басқада әрі қарай талдау жасауға керекті көрсеткіштерді, қарастырылып отырған шешім есептерінен (нәтиже, орнықтылық, шекаралығы) алуға болады. Осы есептерден мақсаттық коэффи-циенттерін және шектеулердің оң жақтарын қанша шамаға кемітуге және өсіруге болатынын, анықтап, олардың өзгеру шекараларын тауып, Excel-дің жұмыс бетіне есептің кестелік моделін шақырып, табылған шекара мәндерін кезек-кезек тиісті ұяларына жазып, Выполнить батырмасын іске қоссақ, Поиск решения бізге жоғарыда қолмен есептелген барлық көрсеткіштерді экранға «автоматты» түрде шығарады. Осыдан кейін кез-келген өндірістік сұрақтарға жауап беру үшін, жан-жақты кеңінен талдау жасай беруге, сөзсіз, мүмкіндік көбірек туады.

Жоғарыда қосалқы және қосымша қосалқы айнымалылары туралы айтылғанда, осы айнымалылар шамалары қандай аралық-тарға дейін сенімді деген сұрақтарды жауапсыз қалдырдық. Ұғымды, зейін қойып оқушы осы кезге дейін бұл сұрақтың жауа-бын тапқан да болар. Дегенмен де, шектеулердің оң жағының 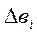– өзгеріс өсімі (кемуі) y_i – қосалқы айнымалылар шамаларының сенім аралықтары, ал мақсаттық коэффициенттердің 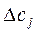– өзгеріс өсімі (кемуі) v_j – қосымша қосалқы айнымалылар шамаларының сенім аралықтары екенін атап өтейік.

Демек, негізгі көрсеткіштер туралы біраз деректер алдық. Өйткені Excel есептерінде келтірілетін көрсеткіштер шамалары, қайдан және қалай есептелінетіні бізге түсініксіз болатын.

Сонымен, ойшыл, іскер-кәсіпкерге керекті кейбір теориялық нұсқауларды талқылауды осымен тәмамдаймыз.

 

 

Шектеулерді талдау

Есептің шешімінде 2-ші және 4-ші өнім мәндері нөлге теңел-ді. Не себепті? Шектеулерді тексерейік. Бірінші шектеу, еңбек қорын модельдеуші теңсіздік (байланысты), қор толығымен қолда-нылған, яғни шектеулі және тапшы (оны орнықтылық есептегі көлеңкелік құнның мәні (69,64) де көрсетіп тұр). Екінші шектеу шикі зат қоры (байланыссыз) шаруашылықтағы басқа қорлармен баланстырылмаған, 1000 бірліктей шикізат пайдалынбай қалды. Үшінші шектеу қаржы қоры, ол да шектеулі (орнықтылық есептегі көлеңкелік құнның мәнінен де (0,268) байқауға болады). Осыдан, шаруашылықтың табылған оңтайлы өнім өндіру жоспары ең тиімді жоспар деп қортындылау әзірше ертерек.

Аталған қорлардан басқа қандай факторлар өндіріс табысына кері әсерін тигізеді? Шаруашылықта қолданбай қалған шикізат-тармен не жасауға болады, оларды қайда жұмсаған пайдалы? Міне осындай сұрақтарға жауап беруге тура келеді.

Жоғарыда аталған қорлардың ішінде ең құндысы еңбек қоры. Осы қорды талқылайық. Қордың көлеңке құны 69,64 тең, яғни шектеудің оң жағын бір бірлікке өсірсек мақсат функция мәні 69,64 ақша бірлігіне өседі. Шаруашылықтағы қорларды, оның ішінде шикізат қорын толық қолдану үшін еңбек қорын қаншаға өсіру керек? Өкінішке орай, орнықтылық есебі бұл сұрақтарға жауап бере алмайды.

Осы шектеудің Допустимое увеличение бағанасында тұрған мәнге қарайық. Ол 200 тең (1.15-сурет), яғни шектеудің оң жағын 1800 дейін көбейтіп, біз сол бұрынғы шешімде қала беруіміз мүмкін. Бірақ, айнымалылардың және мақсат функция мәндері, сөзсіз, өзгеріске ұшырайды. Сонда да, егер еңбек қоры ең жоғарғы шегіне дейін қолданылмаса, онда шектелген және шектелмеген болып, бұрынғы шектеулер қала береді. Ал, егер қарастырылып отырған шектеудің оң жағы 1800-ге тең немесе асып кетсе, онда орнықтылық есебі күрт өзгеріске ұшырайды, яғни осы мезетте есепке шектелмеген басқа шектеулер қатысады.