Главная | Обратная связь

Есепті тапсырыс бойынша шешу 7 страница

1.28-сурет

 

Логикалық шартты есептерді шығару барысында логикалық тізбек тәжірибеде жиі кездеседі. Негізі Excel мұндай тізбекте ЕГЕР функциясын 7 рет қолдануға мүмкіндік береді. Осылай шартты шектеулерді де енгізуге болады.

Шектеулердің сол жағы (СЖ) үшін шартты алғашқы мәлімет-тер мына форматта енгізіледі:

= ЕГЕР(шарт;СЖ1адресі;СЖ2адресі).

Шектеулердің оң жағы (ОЖ) үшін шартты алғашқы мәлімет-тер мына форматта енгізіледі:

= ЕГЕР(шарт;ОЖ1адресі;ОЖ2адресі).

Шектеулердің сол жағы (СЖ) үшін шартты алғашқы мәлімет-терді енгізу мысалы ретінде 1.29-суреттегі мәліметтерге көңіл аударыңыз. Мастер функция f_x - жолында шартты алғашқы мәліметтерді енгізу мына формула: = ЕГЕР(D10>B10;B4*B10+ +D4*D10) арқылы жазылған.

1.29-сурет

 

Егер берілген есептің оң жағынада шарт қойылса, онда тағы да осы әрекеттерге сәйкес амалдар жүргізіледі. Сөзсіз, бір есепте шектеудің оң және сол жақтарына мақсат функция үшін қойылған шарттар бірге енгізіле береді. Сонымен, шартты алғашқы мәліметтер туралы қарастырған оңтайластыруда мүмкіндіктер көп екені, түсінікті деп есептейміз.

 

 

2.Бүтін санды және сызықты емес модельдер

2.1 Бүтін санды модельдер

Тарихи деректер бойынша бүтін санды теңдеулерді шешумен ғалымдар ертеден айналысқан. Мысалға, Гректік математик Диофант (II–III ғ.ғ.) теңдеулердің шешімінде ізделініп отырған белгісіз тек бүтін мәнді болады деп қарастырған. Бүгінгі әдебиет-терде бүтінсанды модельдердің негізін 1932 жылы Венгер матема-тигі Е. Эгервари қалыптастырды делінеді. Ол әрбір ұшақтар жолы-на белгілі бір ұшақтарды бекітумен және әртүрлі жұмыстарға механиктерді бөлумен айналысқан.

Оңтайластыру модельдерін шешу нәтижесінде мәндері ізде-лініп отырған айнымалылар міндетті түрде бүтінсандар болуға тиіс болса, онда мұндай модельдерді бүтін санды программалау мо-дельдері деп атаған. Бүтін сандық шешім тек сызықтық програм-малау есебіне келтірілген кейбір есептерге ғана тән талап емес, шешімнің бүтін санды болуы кейде сызықты емес программалау есептерінде де кездеседі. Сондықтан, егер шектеулер және мақсат функциясы сызықты байланыста болса, онда мұндай есепті сызық-тық программалаудың бүтін санды есебі деп атайды; егер кемінде бір байланыс сызықты емес болса, онда мұндай есепті сызықты емес программалаудың бүтін санды есебі деп атайды.

Халық шаруашылығы есептерінің көбісінде бүтін санды бел-гісіздер кездеседі. Сөзсіз, мұндай сандар физикалық түрде бөлін-бейді, себебі, екі жарым жаңа кәсіпорнын ұйымдастыруға, бір жарым автокөлік сатыпалуға, қырық жарым мал бордақылауға, он жарым жұмыскерді жұмысқа қабылдауға және т.б. болмайды. Сөйтіп, сызықтық программалау есептеріне ұқсас көптеген халық шаруашылық есептеріне бүтін санды шешім қажет. Мысалға, мал табынының тиімді айналымы, ауылшаруашылық техникаларын әр түрлі жұмыстарға бекіту, өндіріс орындарының өндіретін бұйым-дарының тиімді санын анықтау және т.б.с.с.

Бүтін санды программалау есебінің пайда болуын Данциг-тың, Фулкерсонның және Джонсонның “Кесіп тастау” әдісінің идеясымен байланыстырады. Бірақ бүтін санды программалау есебінің бүгінгі дамуы, кесіп тастау идеясын іс жүзіне асыру үшін жасалған Гомори ұсынған бірінші алгоритм пайда болуынан кейін басталды. Бұл әдіс кейіннен Гоморидің атымен, Гомори әдісі деп аталынды. Сонымен, бүтін санды модельдерді шешу әдістерін күрделенген оңтайластыру әдістерінің қатарына жатқызуға болады.

Бүтін санды модельдерді шешу әдістерінің ерекшеліктеріне тоқталайық.

Бүтін санды модельдер сыныбына, айнымалылары теріс емес тек бүтін мәндер қабылдайтын, мақсат функция өзінің аргумент-терімен сызықты байланыста болатын және шектеулерінің сол жағы сызықты теңсіздік немесе теңдік түрінде берілген, бір крите-риялды оңтайластыру есептері жатады. Сонымен қатар айнымалы-лар шамаларына, келесі тақырыптарда қарастырылатын бульдік айнымалыларға қойылатын шектеулер сияқты, қосымша шектеулер қойылмайды Бүтін санды сызықты программалау есебінің жалпы математикалық қойылуын қарастырсақ, осы сынып есептері туралы нақтылы анықтама түсінікті бола бастайды. Демек, жоғарыда кел-тірген анықтама негізінде бүтінсанды сызықты программалау есебінің математикалық моделін мына түрде өрнектеуге болады:

(2.1)

x_j ≥ 0, j = 1,...n, x_j – бүтін сандар, j = 1,..k.

Келтірілген (2.1) жүйенің байланыстарына қарасақ, оның сызықты программалау және оған ұқсас есептерден ешқандайда айырмашылығы жоқ екенін байқаймыз. Дегенмен де, жалғызғана айырмашылық бар. Ол есептің шешімін күрделіндіретін және оған үлкен әсер ететін, мына: x_j – бүтін сандар, j = 1,..k шарты. Бүтін сандар саны k төменгі екі нұсқаның біреуін қанағаттандыруға тиіс.

Егер k = n, мұндағы n – айнымалылардың жалпы саны, онда барлық айнымалылар мәні тек бүтін сан болуға тиіс; мұндай жағдайда есеп толық бүтін санды деп аталады. Егер k < n, яғни тек k дейінгі айнымалылар бүтін санды, ал қалғандары өздерінің шеткі шекаралықтарына дейін кез келген мән қабылдай алатын болса, онда мұндай есептерді жарым-жартылай бүтін санды деп атайды. Осы жерде, толық бүтін санды есептерді шешу үшін барлық бүтін санды айнымалылар жоғары жағынан міндетті түрде шектеулі болу керектігін атап өтейік.

 

 

2.1.1 Бұтақ және шекара әдісі туралы қысқаша түсінік

Бүтін санды есептерді шешуге қазіргі кезге дейін сан түрлі әдістемелер жасалынғаныменен, олардың біреуі де тиімді есептеу процедураларымен қамтамасыз етілген жоқ. Мұндай жағдайлар есептің өлшемі үлкейген сайын ерекше сезіледі, тіпті үлкен қателіктер жіберіледі.

Сонымен, сызықты программалау есептеріне қарағанда бүтін санды программалау есептерін шешу алгоритмдерін компьютермен орындаған кезде біраз қиындықтар кездеседі. Осы қиындықтарды шешумен бүгінгі күнге дейін көптеген жас зерттеушілер айна-ласуда. Олар бүтін санды есептерді шығаруға біраз әдістерді жасап та тастады. Солардың ішінде компьютер тілінде орындауға әжептәуір қызықты және ыңғайлы алгоритм, ол “Бұтақ және шекара” әдісінің алгоритмі. Бұл әдістің алгоритмін ұсынған А. Лэнд және А. Дайг.

Қарастырылып отырған әдістің негізгі идеясы – іздеп отырған шешімді тапқанынша бастапқы көптікті бірінен кейін бірін, бірнеше ішкі көптікке, яғни бұтақтан бұтаққа бөліп, жаңа есептер құрылады да, олардың шешімдерін, яғни барлық ішкі көптіктерде шешімдерді іздейді.

Оңтайлы бүтін санды шешімі табылған көптік бұтақтарға бөлінбейді, оған ақырғы немесе ілініп тұрған бұтақтың ұшының төбесі сәйкес келеді.

Бұл әдіспен есепті шығару үрдісі, Гомори әдісіндегі кесіп тастайтын жазықтар сияқты үздіксіз сызықты программалау есебін шығарудан басталады.

Бір мысал қарастырайық. Мысал, көлемі 20 мың ө.б. (өлшем бірлігі) А және көлемі 38 мың ө.б. Б шикі заттарынан екі түрлі бұйымдар жасалмақшы. Нарықта бірінші бұйымның бір данасын 7 мың теңгеге, ал екінші бұйымның бір данасын 3 мың теңгеге өткізуге болады. Әрбір бұйымның бір данасына, сәйкесінше: А шикі заттынан – (5 және 2) мың ө.б., Б шикі заттынан – (8 және 4) мың ө.б. мөлшерде жұмсалынуға тиісті. Жасалған бұйымдарды нарыққа өткізу арқылы максимальды табыс алу үшін, өндіріс орынына оларды қанша данадан өндірген тиімді.

Шешімі. Бұйымдардың оңтайлы өндіру санын, сәйкесінше x₁ және x₂ деп белгілеп, есептің математикалық моделін құрамыз (1-ші есеп):

Z = 7x₁ + 3x₂ ® max

5х₁ + 2х₂ £ 20,

8х₁ + 4х₂ £ 38,

x₁³ 0, x₂ ³ 0 және x₁, x₂ – бүтін сандар.

Ізделініп отырған айнымалылардың мәні бүтін сан болу шарттын алып тастап, кәдімгі симплекс әдісімен оңтайлы шешімді табылды: х₁

¹=1, х₂ ¹=7,5 және Z¹ =29,5, мұнда айнымалылардың жоғарғы индексі есептің нөмірін көрсетеді.

Шешімде х₂

¹=7,5 – бүтін сан болу шарттын қанағаттандыр-майды. Сондықтан, есепті әріқарай шешу үшін х₂ ¹=7,5 мәні бүтін болуын көздеген, шекаралық шарт қойылған есеп құрамыз. Мұндай шекаралық шарт былай жазылады:

x₂≤7 және x₂≥8

Нәтижесінде, 2-ші есеп.

Z = 7x₁ + 3x₂ ® max

5х₁ + 2х₂ £ 20

8х₁ + 4х₂ £ 38

х₂ £ 7

x₁³ 0 және х₂³ 0.

Симплекс әдісімен шығару нәтижесінде: х₁

²=1,2; х₂ ²=7; Z²=29,4.

Әрі қарай х₁

²=1,2 бүтін санға айналдыру үшін екі есеп шығаруға тура келеді. Біріншіден, 3-ші есепті, мынадай шартпен:

Z = 7x₁ + 3x₂ ® max

5х₁ + 2х₂ £ 20

8х₁ + 4х₂ £ 38

х₂ ³ 8

x₁³ 0 және х₂³ 0

Симплекс әдісімен шығару нәтижесінде: х₁

³=0,75; х₂ ³=8; Z³=29,25.

Шешімде х

₁³=0,75 бүтін сан болмағандықтан, қосымша шекаралық шартты енгіземіз және бірінен кейін бірін, екі есепті тағы да шығарамыз:

4-ші есеп. Z = 7x₁ + 3x₂ ® max

5х₁ + 2х₂ £ 20,

8х₁ + 4х₂ £ 38,

х₁ £ 1 және х₂ £ 7,

x₁³ 0 және х₂³ 0.

Симплекс әдісімен шығару нәтижесінде: х₁

⁴=1; х₂ ⁴=7; Z⁴=28.

5-ші есеп. Z = 7x₁ + 3x₂ ® max

5х₁ + 2х₂ £ 20,

8х₁ + 4х₂ £ 38,

х₁ ≥ 2 және х₂ £ 7,

x₁³ 0 және х₂³ 0.

Симплекс әдісімен шығару нәтижесінде: х₁

⁵=2; х₂ ⁵=5; Z⁵=29.

Сонымен, жоғарыдағы есептердің шешімі бойынша 2.1-кестені тұрғызайық.

2.1-кесте

Көрсеткіштер	Есептер
X1		1,2	0,75
X2	7,5
Z	29,5	29,4	29,25

 

Кестеден көріп отырмыз, 4-ші есептің шешімі, айнымалы-лардың мәндері бойынша бүтін санды, бірақ оңтайлы емес. Өйткені мақсат функцияның мәнін әлі де болса жоғарылататындай бүтін-сандылық шешім бар. Ондай шешімді 5-ші есептен алдық және ол шешім оңтайлы.

Айнымалылар мәндері бүтін санды болу шарты қарастырыл-маған, «Бұтақ және шекара» әдісінің алгоритмі бойынша, 1-ші бөлімде келтірілген тәсілмен, жоғарыдағы қарастырылған әрбір есептің сызықтық модельдерінің MS Excel көмегімен алынған шешімдерді MS Excel-де сценарияға жазайық. Мысалға, 1-ші есептің шешімі алынғаннан кейін Сервис → Сценарии.. бұйрығын іске қосамыз. Диспетчер сценариев сұхбаттасу терезесі ашылады. Добавить батырмасын шертеміз. Название сценария терезесіне сценария атын жазамыз: 1-есеп (2.1-сурет).

 

2.1-сурет. «Бұтақ және шекара» әдісі алгоритмі бойынша бір есептің оңтайлы шешімін табу барысында шығарылған есептер

 

Әрі қарай келесі кезектегі есептің шарттары бойынша кестелік модельге түзетулер енгізіп, Поиск решения құралымен шешімдерді алғаннан кейін, оларды сценарияға жазу әрекеттері қайталанады. Осылай құрылған, барлық есептердің шешім нәтиже-лері, яғни сценария құрлымы 2.1-суретте келтірілген. Суреттен көріп отырмыз, сценария құрлымы толығымен қолмен құрылған 2.1-кес-тедегі мәліметтерді қайталады. Осы процедуралардан кейін алғашқы 1-есеп, айнымалылардың бүтінсан болу шарты (ол тура-лы келесі есепте түсініктеме беріледі) бойынша, MS Excel-де Поиск решения құралында қарастырылған «Бұтақ және шекара» әдісімен қайта шығарылды. Есептің шешім нәтижесі 2.2-суретте келтірілген. Онда жоғарыда жеке-жеке шешілген әрбір есептер «автоматты» түрде бірге қарастырылып, есеп бірден шешілді, яғни ешқандай қиындықсыз оңтайлы шешімді алдық.

2.2-сурет. «Бұтақ және шекара» әдісімен бірден анықталған оңтайлы шешім

Сонымен берілген есепті шешу нәтижесінен “Бұтақ және шекара” әдісі бүтін санды оңтайлы шешімді қамтамасыз ететініне және осы әдіс компьютерде жеңіл орындалынатынына көз жеткіздік. Ең бастысы, осы әдісті тәжірибеде қолдану нәтижесінде, бөлшек мәнді шешімге жай қарапайым «дөңгелектеу» ережесін қолдану, бүтінсанды оңтайлы шешім алуды қамтамасыздандыра алмайды деп қортынды жасалынды.

 

2.1.2 Бүтін санды модельдерді MS Excel көмегімен

шешу алгоритмі

Шартты үздіксіз сызықты модельдерден құралатын есептер симплекс әдісімен, симплекс кестелерін құру арқылы шешілетіні және осы әдістің алгоритмі көптеген пакеттерде компьютер тіліне өткізіліп, программалар құрылғаны белгілі. Осы әдістің, «Әрекет-терді зерттеу» [1], «Математикалық программалау» [16], «Эконо-микалық-математикалық әдістер» [15] және «Менеджментте мате-матикалық әдістер» [12] пәндерінде баяндалған теориясынан, әрбір қадамда кезекті жақсартылған симплекс кесте құрылатыны және осы кесте бойынша нақтылы қарастырылатын белгілер негізінде мынадай сұрақтарға: есепте мүмкін бола алатындай шешім барма және алынған кестедегі мәндер есептің шешімі бола ала ма? және ол оңтайлы ма?, жауап алынатыны айтылған. Есептің шешімі бар болса, онда аталған сұақтарға жауап беретін белгі (ереже бойынша қарастырылатын белгілердің біреу орындалса, онда алынған шешім мүмкін бола алатыны, ал егер екеуі де орындалса шешім оңтайлы делінеді) табылғанша қайта-қайта жаңа сиплекс кестесі тұрғызыла береді. Бүтін санды есептерді шешкенде мұндай белгілер қарастырылмайды, сондықтан кезекті алынған нәтиже бойынша есептің мүмкін бола алатын шешімі алынғанына және шешімнің оңтайлығына жауап алынбайды. Міне осындай қиындықтарға қарамастан, бүтін санды модельді «Бұтақ және шекара» әдісі бойынша шешу қарастырылған MS Excel құралы оңтайлы шешімді нақтылы дұрыс анықтайды.

Бүтін санды модельдерді MS Excel көмегімен шешу бары-сында жасалынатын жұмыстардың реті 1-ші бөлімде баяндалған сызықты модельдерді шешу технологиясымен бірдей. Сонымен қатар есепті шығару барысында, айнымалылар үздіксіз және бүтін санды болған жағдайда олардың нәтижелерінің дәлдігін бағалау үшін есептің шешімдерін салыстыруға болады.

Бүтін санды модельді MS Excel көмегімен шешу технология-сының кейбір ерекшеліктерін мынадай мысал арқылы қарасты-райық.

Төрт түрлі бұйымдарды: A, B, C және D даярлауға үш түрлі қор: еңбек, шикі зат және қаржы қажет, оларды қанша данадан шығару керектігін анықтайық. Бұйымдардың бір данасына есептелінген қорлардың шығындары және бір дана бұйымдардан түсетін пайда 2.2-кестеде берілген.

2.2-кесте. Есептің алғашқы деректері

Қорлар	Бұйымдар	Қорлар мөлшері
A (X1)	B (X2)	C (X3)	D (X4)
Еңбек
Шикізат
Қаржы
Пайда					–

 

Математикалық модель құрамыз, ол үшін мынадай белгілерді қабылдаймыз:

x_j – өндірілетін j – түрлі өнімнің оңтайлы саны,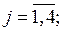

b_i – i – ші қордың шаруашылықта бар мөлшері,

a_ij – i – ші қордың j –шы өнімнің бір данасын өндіруге керекті мөлшері;

c_j – j – шы өнімнің бір данасынан алынатын пайда.

Осыдан есептің математикалық моделі мына түрде жазылады:

(2.2)

x_j ≥ 0, j = 1,2,3,4 x_j – бүтін сандар, j = 1,..4.

MS Excel –дің жұмыс бетіне кестелік модельді құрамыз. Ол үшін мынадай іс-әрекеттер жүргізіледі:

1. Кестелік модельге керекті комментарияларды арнайы ұяларға (2.3-сурет) енгіземіз. Бұл ұялардағы жазулар қарастырылып отырған есептің шешіміне ешқандай да әсер жасамайтынын тағы да ескерте кетейік.

2. B6:E6аралықтағы ұяларғамақсат функция коэффи-циенттерін енгіземіз: с₁ = 60, с₂ = 70, с₃ = 120, с₄ = 130.

3. F6ұяға мақсат функция формуласын енгіземіз: =СУММПРОИЗВ(B4:E4; B6:E6).

4. B9:E11 аралықтағы ұяларға шектеулердің коэффициент-терін енгіземіз.

5. H9:H11 аралықтағы ұяларға шектеулердің оң жағын: b₁ = = 40, b₂ = 75, b₃ = 120 енгіземіз.

6. F9ұяға бірінші шектеудің сол жағының формуласын жазамыз: =СУММПРОИЗВ($B$4:$E$4;B9:E9).

7. F9ұядағы формуланы F10жәнеF11ұяларға белгілі әдіспенкөшіреміз.

8.I9ұясынашектеудің оң жақ бөлігімен сол жағының айырмашылығынбілдіретінформуланы: =I9 – F9 жазамыз.

9.I9ұядағы формуланы, I10және I11ұяларға көшіреміз.

Сонымен Excel-дің жұмыс бетінде қарастырылып отырған есептің кестелік моделінің сыртқы пішіні 2.3-суретте көрсетілген.

Есепті әрі қарай шешу үшін Поиск решения шақырылады. Ол үшін бас менюдан: Сервис Þ Поиск решения...

Сұхбаттасу терезесінде Поиск решенияпайда болғаннан кейін төменгідей іс-әрекеттер орындалынады:

2.3-сурет. Бүтін санды есептің кестелік моделі

1. Установить целевую ячейкужолына мақсаттық ұяның абсолюттік $F$6адресін көрсетеміз, яғни курсорды мақсат функция формуласы жазылған ұяға орналастырамыз.

2. Равной:тобы үшін, максимальному значению –нұсқасын іздеуді таңдаймыз.

3. Изменяя ячейкижолынамәндері ізделінетін айнымалы-лардың абсолюттік $B$4:$E$4адрестерін енгіземіз.

4. Келесі кезекте шектеулерді, айнымалылардың төменгі және жоғарғы шектерін, теріс болмау және бүтін санды болу шарттарын енгіземіз. Осы мақсаттарға жету үшін келесідей іс-әрекеттер орындалынады:

· шектеулерді енгізу үшін Поиск решения-ныңалғашқы сұхбаттасу терезесіндегі Добавить батырмасын басамыз (2.4-сурет);

· қосымша пайда болған сұхбаттасу терезеде Ссылка на ячейку: жазуының астындағы терезеге $F$9:$F$11ұялар аралығыбейнеленеді;

· шектеулердің жиналып тұрған белгілері тізімдерінің ішінен кестелік модельде көрсетілген белгіні “<=” таңдаймыз;

· Ограничение: жазуының астындағы терезеге $H$9:$H$11аралықтарында тұрғанұялардағы шектеулердің оң жақтары енгізіледі;