 |
|
Есепті тапсырыс бойынша шешу 3 страница
Айнымалылар саны – n және шектеулер саны – m мен анық-талынатын оңтайластыру есептерінің өлшем бірлігі, оның маңызды сипаттамасы. Сондықтан шешім қабылдау үшін тәжірибелік жағдайда өндірістік есептерді құрған кезде осы екі көрсеткіштер қатысына ерекше көңіл аударған жөн. Егер n < m, онда есептің шешімі жоқ; n = m – есептің жалғыз ғана шешімі болады, яғни оңтайластрудың мағынасы болмайды; n > m – есептің шешімі өте көп есеп мағыналы деп саналады.
Егер есептің барлық шектеулері теңсіздік түрінде болса, онда оңтайластыру есебі барлық жағдайда мағыналы. Себебі негізгі хi айнымалылар саны (n) теңсіздіктерді теңдікке түрлендіре-тін қосымша уi айнымалылар санына, яғни шектеулер (m) санына (N=n+m) өседі. Нәтижесінде, барлық жағдайда: N = n+m > m, яғни есептің шешімі өтекөп болады.
Сонымен, N = n + k >m шартының орындалуы оңтайлаудың негізгі талабы екенін әрқашанда есте ұстағанымыз жөн. Мұндағы k–шектеулер жүйелеріндегі теңсіздіктер саны.
СП модельдерін шешу әдістері туралы [12, 15, 16 және 19] әдебиеттерде кеңінен жан-жақты баяндалған. Сондықтан оқу құра-лында қарастырылатын модельдердің математикалық теорясына және шешу әдістеріне көп көңіл аударылмайды. Біздің негізгі мақсат «Шешім қабылдау» мәселесінде белгілі математикалық әдістермен модельдерді қалай қолданады, яғни осы тұрғыда олар келесі бөлімдерде қарастырылады.
1.3 MS Excel - де оңтайластыру есебтерін
шығарудағы алғашқы қадамдар
MS Excel-де құрылған математикалық модельмен қандайда бір есептеулерді орындаудан бұрын, оны Excel-дің жұмыс бетіне бір ретпен ауыстырады (жазады). Ол үшін қандай ұяларда айнымалылар орналасатынын анықтап, мақсат функцияны және шектеулер функцияларын (сол жағын) есептейтін формулаларды керекті ұяларға жазып, сонымен қатар бөлек ұяларға шектеулердің оң жағын жазу керек. Excel-дің жұмыс бетінде ұяларда белгіленген мәндер және жазылған белгілер мен формулалардың барлығы бірге кестелік модель деп аталады. Шындығында бұлай аталу модель туралы ұғымды толық білдірмейді, тек оның математикалық модельмен есептеулер жүргізу үшін Excel-дің жұмыс бетінде кесте сияқты ыңғайлы орналасуының қажеттілігінен туындайды.
Оңтайластыру есептеріне кестелік модель құру жөнінде жал-пы қабылданған маңызды ереже жоқ. Дегенмен де Excel-де оңтай-ластыру есептердің кестелік модельдерін құрғанда нақтылы бір принциптерді және келешекте Поиск решения құралын қолда-нуды жеңілдететін келесідей ұсыныстарды ескерген жөн.
· Айнымалылардың мәндері бөлек бір ұяларда орналас-тырылады және бөлек ұялар блоктарында топтастырылады.
· Кестеде әрбір шектеулерге бөлек жол немесе бағана бөлінеді. Шектеулер бөлек ұялар блоктарында топтастырылады.
· Мүмкіндігінше айнымалылардың, мақсат функция мән-дері сақталатын ұялардың және шектеулердің тақырыптары, соны-мен қатар кестелік модельдің бас тақырыбы болғаны жөн.
· Мақсат функция коэффициенттері сәйкес айнымалы-лардың астына немесе үстіне орналастырылып, бөлек жолда сақта-лады; мақсат функцияны есептейтін формула көрші ұяда тұруға тиіс.
· Әрбір шектеулердің коэффициенттері тұрған жолдың оң жағындағы шеткі ұяда (шектеудің сол жағының формуласы жазылған) сол шектеудің есептелген мәні жазылады. Осы жолда одан кейінгі ұяда шектеу белгісі (“>=” немесе “<=” немесе “=”) және келесі ұяда шектеудің оң жағы жазылады. Мүмкіндігінше шектеудің оң жағы формула емес, тұрақты шама болғаны дұрыс. Келесі ұяға шектеудің оң және сол жағының айырымын қосымша көрсетуге болады.
· Поиск решения құралының сұхбаттасу терезесінде айнымалылардың теріс болмау шарты белгіленеді. Сондықтан айнымалылардың теріс болмау шартын кестелік модельге енгізу міндетті емес.
Осы нұсқауды бұлжытпай орындаған жағдайда модельдің барлық негізгі коэффициенттері бөлек ұяларда орналасады. Сон-дықтан, модельдің формулаларын өзгертпей, оларды керек кезінде жеңіл өзгертуге болады. Айнымалыларды немесе шектеулерді көр-сету үшін ұялар аралығын, яғни айнымалыларды немесе шектеу-лерді жеке-жеке енгізбей, топ-тобымен енгізуге (ұялар аралығы-мен) болатындықтан, оларды топтастыру нәтижесінде Поиск решения құралымен жұмыс жасау жеңілдетіледі. Кестелік модельде тақырыптардың (комментариялар) болуы, оның кез кел-ген қолданушыға түсінікті болуын қамтамасыздандыру және есеп-ті құжаттау үшін қажет.
Кестелік модельдің соңғы жолдарының біріне бөлек «Шеші-мі» жолын қарастырған біршама ұтымды. Біріншіден, айнымалы-лардың шешімі және мақсат функция мәні бірге жиналып тұрса, қарастырылып отырған модельді құжаттандыру ыңғайлы. Оларды түсіндіретін өлшем бірліктерін көрсететін жазулар жазуға және сан мәндердің бөлшек жағын керекті дәлділікке дейін көрсету үшін айрықша форматтауға болады. Екіншіден, математикалық модельде айнымалылардың коэффициенттері әртүрлі мәнде немесе шешім мәндері әртүрлі (мысалға, бірнеше қатардан тұратын бүтін және үтірден кейін бірнеше қатардан тұратын бөлшек сандар) болса, онда оларды керекті бөлшегіне дейін және мақсат функция мәнін бір ретке түзетіп, масштабтауға тура келеді. Осындай әрекеттерден кейін «Шешімі» жолында, кестелік модельдің «есептеу» бөліміне тиіспей, нақтылы есепке алынатын мәндерді керекті қалпына келтіруге мүмкіндік туады.
Кестелік модельге мәліметтерді жедел енгізуге автоматты көшіру әрекеті бірәз көмек береді. MS Excel-де көшіру процедура-лары өте көп. Солардың ішінен оңтайластыру есептерін шешуде жиі қолданылатындары: панель құралдары көмегімен көшіру, тыш-қан көмегімен көшіру, сүйретіп көшіру және адрестерін сақтай отырып көшіру. Осы көшіру тәсілдерінің ең қарапайымы, ол панель құралдарымен көшіру. Ол әрбір компьютерді пайдаланушыға белгілі.
Тышқан көмегімен көшіру тәсілінің алгоритмі:
– көшірілетін объектіні белгілейміз;
– курсорды объектінің шетіне апарамыз;
– “Ctrl” – батырмасын басып жібермейміз. Экранда, курсор стрелкасына “+” белгісі қосылады;
– тышқанның сол жақтағы батырмасын басып, жібермей, курсорды көшірілетін ұяға дейін жылжытамыз;
– тышқанның және “Ctrl” батырмаларын босатамыз. Экранда көшірілген объект жаңа орнында;
– белгіні алып тастаймыз.
Сүйретіп көшіру алгоритмі, бір ұядан тексті немесе санды (мысалға, №5) көрші келесі ұяларға көшіргенде қолданылады. Көшірілетін объектіні оңға немесе төмен сүйреткенде, онда тұрған санға, әрбір көрші жаңа ұяда 1 қосылып отырылады (мысалға, №6, №7, ...), ал солға немесе жоғары сүйреткенде, керісінше 1 кемиді (мысалға, №4, №3, ...)
– көшірілетін ұяны белгілейміз;
– белгіленген ұяның төменгі оң жақ бұрышына курсорды апарамыз. Экранда курсор ұшында қара крест пайда болады;
– тышқанның сол жақтағы батырмасын басып, жібермей, ақырғы көшірілетін ұяға дейін жылжытамыз;
– тышқанның батырмасын босатамыз. Экранда барлық көрші және ақырғы ұяларда сандары бірге өзгерген, көшірілген объекті.
Адрестерін сақтап көшіру. Оңтайластыру есептерін шыға-руда, аргументтері ұялардың адрестері болып есептелінетін функциялар жиі қолданылады. Мысалға, А1 ұяда мына формула тұрсын:
А1=В1+5.
Егер осы ұяны Е2 ұяға көшіретін болсақ, онда мынаны көреміз:
Е2=А2+5.
Ұялар адрестерінің көшіру кезінде мұндай өзгерісі, олардың жаңа адреске автоматты түрде бейімделуі делінеді.
Егер көшіру нәтижесінде ұяның адресі ешқандай өзгерізсіз сақталынатын болса, мұндай жағдайда көшірлетін ұяның адресіне $ символын енгізу керек. Бұл кезде мына ережелер ескерілгені жөн:
– символ мына түрде жазылса $A1, көшіру нәтижесінде бағананың ғана аты сақталады;
– символ мына түрде жазылса A$1, көшіру нәтижесінде жолдың нөмірі сақталады;
– символ мына түрде жазылса $A$1, көшіру нәтижесінде бағананың аты және жолдың нөмірі сақталады.
1.4 Модельдер шешімін талдаудың өзектілігі және
тәжірибеде керекті нақтылы көрсеткіштер
Медицинада ауру адамды алдынала зерттеп және оны талдап, бір шешімге келмейінше ешқандай ауруға диагноз қойылмайды және емдеуге қажетті дәрі-дәрмектер қолданылмайды, яғни «Шешім қабылдау» мәселесі жауапты. Өкінішке орай, өндірісте басқару жұмыстары, оның ішінде экономикалық және техникалық жағдайларды басқаруда «Шешім қабылдау» мәселесіне онша ма-ңызды мән берілмей, оның кейінгі, түпкі әсері ескерілмей қалады. Әрине, не себепті олай, оның себеп салдары көп, бұл жерде оның бәріне тоқталудың қажеті жоқ. Қазіргі нарық жағдайында негізінде қандай істе болмасын, алдынала талдаусыз шешім қабылдауға болмайды.
Талдау жасаудың қуатты құралы, ол математикалық модель. «Бір рет ату үшін мылтық сатып алуға болмайды» демекші, ізделі-нетін белгісіздердің тек бір мәнін анықтау үшін математикалық модель құруға болмайды. Ол үшін күрделі формулаларды терең ойластыра отырып, оны құрып, және соңында онымен бір ғана есептеу жүргізудің қажеті жоқ.
Негізінде математикалық модель, оңтайлы шешім қабылдау кезінде пайда болатын көптеген сұрақтарға жауап алуда қолданы-латын, өте қызықты құрал.
Математикалық модель негізінде жүргізілетін талдау түрлері 1.2-суретте келтірілген. Суреттегі кейбір сұрақтарды түсіндіріп көрелік.
Есепті қойған кезеңде мынандай: «не болады, егер...? және/немесе «не керек, мына...?» және т.б.с.с. сұрақтарға жауап беру үшін талдау жүргізіледі.
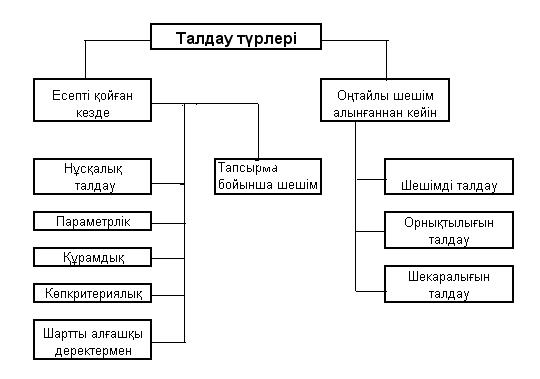
1.2- сурет. Шешілетін есепті талдау түрлері
Бірінші сұраққа жауап беру үшін жүргізілетін талдау, нұсқа-лық талдау деп аталады, ал екіншіге – тапсырыс бойынша шешім-дермен делінеді.
Нұсқалық талдаудың 1.2-суретте келтірілген түрлері:
· Есепті оның кейбір параметрлері арқылы шығарып, шешімге талдау жүргізу, параметірлік талдау делінеді. Оқулықта параметірлік талдауға бірнеше мысалдар келтіріледі.
· Оңтайластыру есебін шектеулердің әртүрлі құрамында шешу нәтижесін талдау жұмысын құрамдық талдау деп атайды.
· Есепті әртүрлі мақсат функцияларымен шешіп, нәтижені талдау, көп критериялы талдау делінеді.
· Егер есепті шешуге керекті алғашқы деректер, қосымша шарттың талаптарын дұрыс орындауға байланысты болса, онда мұндай талдау, шартты алғашқы деректермен талдау делінеді.
Берілген тапсырма бойынша есептің шешімін табу, есепті талдаудың екінші тобына жатады. Оның мақсаты, айнымалылар-дың, шектеулердің сол жағының немесе мақсат функцияның беріл-ген мәндерінде есептің шешімін іздеу.
Есепті қойған кезеңдегі талдаумен қатар, 1.2-суретте келті-рілген талдаулардың ішіндегі оңтайлы шешім қабылдауға ең қажетті және қуаттысы, ол оңтайлы шешімді талдау болып есептеледі. Оңтайлы шешімді талдаудағы орындалынатын жұмыс-тар 1.2-суретте де келтірілген және оларды орындау үшін оқушылардың қазақ тілінде жазылған алғашқы оқулықтармен оқу құралдарынан [12, 13, 15 және 16] немесе орыс тіліндегі әдебиет-терден [1 және 2] арнайы теориялық түсініктерді білгені жөн. Сондықтан әрбір жаңа тақырыптарды керекті теориялық мәлімет-терді қысқаша еске түсіруден бастаймыз.
1.4.1 Шешімнің сезімталдылығын талдау
Сонымен математикалық модельдің шешімі алынды. Енді біз онымен не істейміз, бірден өндіріске енгіземіз бе? Жоқ, әзірше ерте. Қойылған мәселенің әзірше нақтылы моделі үшін ғана шешім алдық, ал негізгі мәселе «өндірістік шешім қабылдау» әлі шешіл-ген жоқ. Модельді құру барысында, оны қарапайымдату мақсатта, біз бірәз көрсеткіштерді жуықтап алдық, сөзсіз, кейбір байланыстар ескерілмей де қалуы мүмкін, көптеген маңызды емес факторлар әдейі алынып тасталынды және байланыстар бір шама жеңілде-тілді. Сөйтіп, біз қойылған есепті реттедік, математикалық тілде мұндай әрекеттерді формалдау деп атайды. Сонымен, егер кейбір көрсеткіштердің тәжірибедегі нақтылы мәндері, модельде енгізіл-ген мәндерінен аздаған айырмашылықтар болса, онда шешімде олар қаншаға өзгереді немесе өзгермей ме? Осындай және осылар сияқты сұрақтарға алынған шешімді талдау нәтижесінде жауап беруге біз міндеттіміз. «Ғылым» тілінде мұндай талдау сезімтал-дылдықты талдау деп аталады. Осындай талдауда, нақтылы си-туацияда, шешім қабылдауда қолданылатын, маңызды ақпараттар алынады. Талдау, математикалық модельмен оңтайлы шешім алын-ғаннан кейін, жүргізіледі.
Сезімталдылықты талдауда төмендегідей сұрақтарға жауап-тар алынады:
· Алынған шешімді сақтай отырып, модельдің параметр-лері қандай шектерге дейін өзгере алады?
· Қандай шектеулер мақсат функциямен байланысты (яғни мақсат функцияны шектейді (ұстап қалады)), ал қандай шектеулер байланыссыз (яғни есептің шешіміне әсер етпейді).
· Егер байланысты шектеулердің оң жағын өзгертсек, онда мақсат функция қалай және қаншаға өзгеруі мүмкін?
· Егер есептің оңтайлы шешімінде бір айнымалы нөлге тең болса, онда ол қандай шартта оң мәнді қабылдаған болар еді? (Өндірістік есептер үшін аталған сұрақтар өте өзекті сұрақ-тар).
Бірден ескертейік, есептің шешімі арқылы толық сезімтал-дылықты талдау, күрделігі бойынша оңтайластыру есебінің шешу әдістерімен де теңеспейтін, олардан көп жоғары, арнайы әдістерді қолдануды қажет ететін, өте ауыр және қымбат жұмыс.Сондықтан, төмендегі бірінші мысалдан кейін келесі тәжірибелік мысалдарды қарастырғанда бұл талдауға терең тоқталмай, қысқа-қысқа негізгі көрсеткіштерді баяндаймыз. Келесі мысалда мүмкіндігінше осы талдауға кеңірек тоқталамыз. Мұндай талдаулар жүргізуге тағыда Поиск решения құралы көп мүмкіншілік тудыратынын, ол есептің шешімінің нәтижесі, орнықтылығы және шекаралығы бойынша есеп беретінін атап өтейік.Поиск решения құралының осындай әрекеттерін техникалық тілде генерациялау деп атайды.
СоныменПоиск решения құралы талдау жасауға мүмкінші-лік тудырады, ол есептің шешімінің 1.2-суретте көрсетілген үш түрлі есебін: шешім нәтижесін, орнықтылықты және шекаралы-ғын генерация жасайды. Аталған есептер тек сызықтық модель-дерді шығарғанда ғана генерацияланады. Бүтін санды модельдерде орнықтылық және шекаралығы есептері генерацияланбайды, ал сызықты емес модельдерде орнықтылықтылық бойынша есеп басқа түрде қалыптасады (генерацияланады).
1.4.2 Нұсқалық талдау
Қорларды оңтайлы қолдануды жоспарлау барысында ең қы-зықтысы нұсқалық талдаудың екі есебін шешуде:
– параметрлердің біреуінің әртүрлі мәндерінде есепті шешу және параметрлік талдау жүргізу;
– бірнеше мақсат функция бойынша шешімдерді іздеу.
Есепті бірнеше мақсат функциялар арқылы шешкенде екі қойлымның біреуі болуы мүмкін: алынатын нәтижені берілген қорлар мөлшерінде максимальдау немесе берілген нәтижеде қолда-нылатын қорлар мөлшерін минимальдау.
Егер қорлар мөлшерін K– деп, олардың қолдану нәтижесін H – деп белгілесек, онда H=f1(xj) және керекті қорлар мөлшері K=f2(xj), мұндағы xj – j-өнімнің оңтайлы мөлшері деп есептесек, есептің осы екі қойлымдардағы математикалық модельдері былай жазылуы мүмкін:
– бірінші қойлымда:
F1=H → max
H=f1(xj) және K=f2(xj)
K≤ Kберілген
gj ≤ xj≤ Gj , j=1,…,n,
– екінші қойлымда:
F2=K → min
H=f1(xj) және K=f2(xj)
H≤ Hберілген
gj ≤ xj≤ Gj , j=1,…,n.
мұндағы j-өнімнің gj – төменгі және Gj – жоғарғы өндіру шегі, n–өндірілетін өімдер түрлерінің саны.
Тәжірибеде осы екі қойлымда есептерді шығару тәсілдерін «Бірнеше мақсат функция бойынша шешім» тақырыбында қарасты-рамыз.
1.4.3 Қосалқылық теориясын қолдану арқылы есепті талдау
Қорларды оңтайлы қолдануға арналған есептің математи-калық моделін қарастырайық.
Мақсат функция:

мына шектеулерде:

Осы есептің қосалқы есебі:

мына шектеулерде:
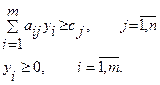
Қосалқылықтың бірінші теоремасы. Егер қосалқы жұп есептердің біреуінің оңтайлы жоспары болса, онда екіншісінің де оңтайлы жоспары болады және мақсат функцияларының мәндері осы оңтайлы жоспарда бір-біріне тең, яғни Zmax = Fmіn.
Егер Z®max (қосалқы есеп үшін F®mіn), ал шектеулердің түрі: “£” (қосалқы есеп үшін “³”) немесе Z®mіn, (қосалқы есеп үшін F®max), ал шектеулер “³” (қосалқы есеп үшін “£” ) түрде жазылады, керісінше жағдайда есептің шешімі жоқ.
Қосалқылықтың 2-ші теоремасы. Тек мына қатынастар орын-далғанда:


бастапқы есептің жоспары 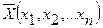 және қосалқы есептің жоспары
және қосалқы есептің жоспары  оңтайлы делінеді.
оңтайлы делінеді.
Осы көрсетілген жағдай, бір-бірімен қосалқыланған екі есептің біреуінің оңтайлы шешімі бойынша екіншісін анықтайды.
2-ші теореманың маңызы: егер қосалқы бағалар уі>0, онда қорлар жетімсіз (яғни олар толығымен қолданылған, ал олардың қолданбаған мөлшерлері Si=0). Егер уі=0, онда і-қор мөлшері артық, сондықтан Si>0. Егер уі<0, онда оңтайлы мәні ізделініп отырған і-айнымалының мәні ең шеткі төменгі шегіне тең, оның бір бірлікке өсуі мақсат функция мәнін қосалқы бағаның мәніне кемітеді.
Қосалқылықтың 3-теоремасы. Қосалқы есептің оңтайлы шешіміндегі yі-ң мәні, бастапқы есептің шектеулерінің бос мүше-лерінің (bі) мақсат функцияға әсерлігінің бағалары, яғни егер bі®Dbі бірлікке өзгерсе, мақсат функция (DZ) қаншаға өзгеретінін көрсетеді немесе математикалық түрде:
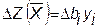 ,
,
мұндағы yі – bі-ң қосалқы бағасы (тәжірибеде өте маңызды көрсеткіш. Оны өндірістік қордың жалпылама объективті бағасы немесе көлеңкелік құны немесе құндылығы деп атайды).
Қосалқылықтың 3-теоремасынан:
 ,
,
мұндағы  онда
онда  . Осы теңдіктен, егер есеп қорларды оңтайлы қолдануға бағытталған болса, онда і-қордың мөлшерінің өзгеруі мақсат функция мәнінің сызықты байланыста өзгеруін көрсететінін байқауға болады.
. Осы теңдіктен, егер есеп қорларды оңтайлы қолдануға бағытталған болса, онда і-қордың мөлшерінің өзгеруі мақсат функция мәнінің сызықты байланыста өзгеруін көрсететінін байқауға болады.
Егер yі-мәні аз мөлшерде болса, онда і-қор мөлшерінің шама-лы өзгеруіне оңтайлы табыс мәнінің аздап қана өсуі сәйкес келеді, яғни і-қордың құндылығы онша көп емес.
Егер yі = 0, онда і-қор мөлшері көбейсе де оңтайлы табыс мәні өзгермейді, себебі осы қордың өндірістегі құндылығы нөлге тең, яғни қор құнсыз. Шындығында да, егер шикізаттың (қордың) мөлшері өзіне қажеттілік мөлшерден көп болса, онда оның қажет-тіліктен қалған бөлімі өндіріске керек емес, яғни ол құнсызданады және оны нөлге теңестіреді.
Егер yі- мәні көзге түсетіндей жоғары болса, онда і-қоры мөлшерінің шамалы өзгерісі оңтайлы табыс мәніне көп өзгерістер тудырады, яғни і-қорының өндірісте құндылығы жоғарлайды. Осы қор мөлшерінің азайуы өндірілетін өнім көлемін көп төмендетеді.
Сонымен, уі-айнымалысы і-қорының құндылығының сипат-тамасы деп есептелінеді. Мысалға, і-қор мөлшері бір бірлікке өссе (Dbі=1) оңтайлы табыс мәні yі- бірлігіне өседі. Сондықтан yі-ді қордың «Шартты құны», і-қоры бірлігінің бағасы, жалпылама объективті баға ретінде қарастырады.
Қосалқы баға yі-оңтайлы табыстың і-қоры бойынша жекелен-ген туындысы, сондықтан ол, і-қор мөлшері өзгеруіне байланысты оңтайлы табыс мәнінің өзгеру жылдамдығын сипаттайды. Сонымен қатар, yі-бойынша мақсат функцияның мәніне шектеулер қандай дәрежеде әсер ете алатынын анықтауға болады.
Қорлар мәнінің қандай өзгеру аралықтарында олардың құн-дылығы (уі) өзгерізсіз қалатынын мына формулалармен анық-тайды:

мұндағы хj–оңтайлы шешімдегі айнымалылардың мәні;