Главная | Обратная связь

Дискреттік программалау модельдері

Бульдік айнымалыларды пайдаланып шығарылатын тәжіри-беде жиі кездесетін маңызды есептердің бірі дискретті програм-малау есептері. Олар, есептеу объектісі және факторлары физи-калық түрде бөлінбейтін есептер. Ізделініп отырған айнымалылары тек бүтін мәндер қабылдайтын (мысалға, штаттық расписанияны жоспарлау және мәндері нөль немесе бір болатын логикалды немесе бульдік айнымалы жұмысқа тағайындау есептері) есептерді жатқызады. Сонымен, мұндай есептердің ерекшеліктері және екілік айнымалы есептерден айрықшылықтары былай түсіндіріледі: оңтайластырудың нәтижесінде оңтайлы мәндері ізделініп отырған айнымалылардың өзгеру аралығында кез келген үздіксіз мәндерінің бірі емес, тек олардың берілген нақты мәндерінің ішіндегі біреуі оңтайлы болуы мүмкін. Сондықтан мұндай сандар бүтін немесе бөлшек сандарда болады.

Дискретті программалау есептеріне бір мысал қарастырайық.

Мысал. Формасы параллелипипед болып келетін бактың сиымдылығы максимальды болатындай, табанының ені (a) және ұзындығы (b), сонымен қатар биіктігінің (h) ұзындықтарын табу керек.

Бак жасауға, ені: a = 4,25; 5,5 және 6,75 м, материалдарды қолдану ұсынылды. Материалдардың бағасы: С = kS =100 мың теңге, мұндағы k – 1 м² материалдың бағасы k =10 мың теңге, S – бак жасауға кеткен материал, м².

Есептің математикалық моделін құрамыз. Бактың көлемі:

V = abh, м³.

Бак жасауға керекті материалдың ауданы:

S = 2 (ab) + 2 (a +b)h = 2 (ab + (a + b)h), осыдан аламыз

С = kS =2 k(ab + (a + b)h).

Осындай әрекеттерден кейін есептің оңтайластыру моделін құрамыз:

V = abh → max

Берілген материалдардан жасалған максимальды сиымды бактың құны берілген бағадан (С_бер) көп болмауға тиіс:

2k (ab + (a + b)h) ≤ С_бер,

a, b, h ≥ 0 және a 4.25; 5.5; 6.75.

Есептің шарты бойынша бактың бағасы С_бер =100 және k = =10 мың теңге екенін ескерсек, онда бірінші теңсіздікті былай жазуға болады:

2∙10 (ab + (a + b)h) ≤ 100 немесе ab + (a + b) ≤ 5 (a)

Осыдан кейін бульдік айнымалылар арқылы математикалық модель мына түрде жазылады:

a = 4,25δ₁ + 5,5 δ₂ + 6,75 δ₃ немесе

a - 4,25δ₁ - 5,5 δ₂ - 6,75 δ₃ = 0 (б)

δ₁ + δ₂ + δ₃ =1 (в)

0 ≤ δ_j ≤ 1, j = 1, 2, 3.

δ_j – бүтін, j = 1, 2, 3.

 

Сонымен сызықты емес оңтайластыру моделі құрылды. Есепті MS Excel–де шығарамыз. Жұмыс бетіне барлық деректерді жазып, кестелік модель тұрғызамыз. Ол үшін B2:G2 аралықта мәндері ізделініп отырған (бульдіктермен қоса) айнымалылардың белгілері, E4:G4; E5:G5 және E6:G6 аралықтарда бульдік айнымалылардың төменгі және жоғары мәндері, сонымен қоса олардың бүтін сандар болу шарттары жазылды (2.14–сурет).

 

2.14-сурет

 

Жоғарыда сызықты емес программалау есебінің математи-калық моделі құрылғаны аталды. MS Excel көмегімен сызықты емес программалау есебін шығару тәсілінде сызықты програм-малау есебіне қарағанда мынадай өзгешеліктер бар:

– барлық ізделінетін айнымалыларға бастапқы мәндер тағайындалынады;

– Поиск решения–ның Параметры–де Линейная мо-дель–ді іске қосудың қажеті жоқ.

Бірінші талапты қамтамасыздандыру мақсатында B3:G3 аралыққа 1 жазамыз (2.14-сурет).

H9 ұяға мақсат функция формуласы: =B3*C3*D3, сонымен қатар H10, H11 және H12 ұяларында, сәйкесінше (а), (б) және (в) шектеулер формулаларының сол жағы: =B3*C3+(B3+C3);

=СУММПРОИЗВ (E11:G11;$E$3:$G$3) +B3 және

=СУММПРОИЗВ(E12:G12;$E$3:$G$3) жазылады.

Поиск решения құралында мақсат функция ұясының адресін және бағытын, айнымалылар ұяларының аралығын және шектеулерді енгізгеннен кейінгі сұхбаттасу терезесінің бейнесі 2.15-суреттегідей болады.

2.15-сурет

 

2.16-сурет

Сызықты емес программалау есебін шығару тәсілінің екінші талабы бойынша Парамер-дің сұхбаттасу терезесі 2.16-сурет-тегідей қалыпта қалады.

Выпонитьбатырмасын басқаннан кейін есептің шешімін аламыз (2.17-сурет).

2.17-сурет

Алынған шешімнен параллелипипед формалы бактың а қабырғасы тең 4,25 м (a = 4,25 м), ал қалған қабырғаларының ұзындықтары бірдей және тең: b=h=0,55 м. Анықталған қабыр-ғаларының оңтайлы ұзындықтарында бактың сиымдылығы максимальды және тең: V= 1,2966 м³ .

Бактың а қабырғасының ұзындығы (4,25, 5,5 және 6,75 м) берілген және математикалық модельде олар туралы қосымша шектеулер қарастырылғандықтан, табылған бактың сиымдылығы, есепті қосымша шектеусіз шығарған сиымдықтан азаяды.

Сонымен, дискреттік программалау көмегімен алдын ала берілген мәндердің ішінен экстремальдық мәнге жетуге ықпал жасайтындай бір мәнді алуға болады, бірақ мұндай әдістен мақсат функция жақсармайды.

Дискретті программалау есептерін шығару барысында тек нәтиже бойынша есеп (Отчет по результатам) алынады. Онда ешқандай да жаңа деректер болмайды, сондықтан оны талдау қажетсіз. Нұсқалық талдау қалай жүргізілетініне тоқталсақ, олда сызықты емес программалау есептерінде қолданылған тәсілдер арқылы жүргізілетінін байқаймыз. Дискреттік программалау есеп-терін шығарғанда параметрлік талдау біраз қызықты. Мысалға, 2.18-суретте қарастырылып отырған есептің ізделіп отырған пара-метрлері (бактың қабырғаларының ұзындығы) үздіксіз (есепті бульдік айнымалыларысыз шешу) және үздікті (яғни дискретті программалау есебі құрылып, бірнеше мәндердің ішінен бір мәнді, бульдік айнымалылары арқылы таңдау) болған жағдайда нәтиже-лерді салыстырыу үшін сценария кестесі келтірілген.

 

2.18-сурет

Ескерту: параметрлік талдауда жасалынған жұмыстар жоғарғы бөлімде жан-жақты баяндалуына байланысты, 2.18-суреттегі қорытынды сценарияны қалыптастыру жолына терең тоқталмаймыз.

2.18-суретте келтірілген деректерден көріп отырмыз, алғаш-қы бағалары әртүлі бактардың көлемі, олардың параметрлері үздіксіз болған жағдайда дискреттік программалау талаптарымен анықтаған мәндерге қарағанда біраз жоғары. Бірақ, жобаланып отырған бактың бағасы өскен сайын, оның екі нұсқада есептелген максимальды сиымдылықтарының қатынасы бірге ұмтылатыны байқалады.

Сонымен, осындай және барлық шығарылатын есептер үшін де, жоғарыда келтірілген тәсілмен талдаулардың жасалуы, оңтайлы шешімдерді қабылдауда өте керекті пайдалы құрал екеніне айрықша көңіл аудару керектігін атап өтейік.

 

 

2.2 Сызықты емес модель

«Димаш» атты компания номенклатуралық топтағы үш түрлі А, Б, В бұйымдарды шығарады. Осы бұйымдар бір өндіріс орнында бір жабдықтармен жасалады және жабдықтың жалпы жұмыс қоры бұйымдарды өндірген уақыттар сомасынан құралады. Сондықтан осы бұйымдардың шығару мөлшерлері бір-бірімен тығыз байланысты. Компания экономисі бір топтағы осы бұйымдардың жалпы өндіру құны, бір-бірінің өндірілген сандарымен (х_а, х_б және х_в) мынадай эмпириялық байланыста болатынын анықтады:

С = 200х_а + 600х_б + 400х_в - 100х_ах_б -50х_бх_в+ 150х_ах_в, теңге

Сонымен қатар, бұйымдардың сату құны, олардың өндірілген санына байланысты болатыны, яғни бұйымдар көп өндірілсе соғұрлым сату құндары төмендейтіні анықталды. Осы заңдылық-тардың эмпириялық модельдері статистикалық деректер арқылы тұрғызылды, яғни бір дана i-бұйымының құны:

Ц_а = 750(2 - х_а/500), теңге,

Ц_б = 1000 (2,5 - х_б/500), теңге,

Ц_в = 1500 (1,5 - х_в/500), теңге,

Өндіріс орнындағы жабдықтың қуаты, егер бұйымдардың барлық түрін бір уақытта шығаратын болса, онда олардың 500 данасын ғана шығара алады. Осы жағдайда өндіріс максималды пайда табу үшін компанияға әрбір бұйымдарды қанша данадан шығарған тиімді екенін табу керек.

Шешу. Есептің математикалық моделін құрамыз. Есепте қойылған мақсатқа жауап беретін айнымалылар: х_а, х_б және х_в – белгілі, яғни жасалынатын А, Б, В бұйымдардың оңтайлы мөлшері. Тапқан пайданы (Z) есептейтін мақсат функцияны тұрғызамыз.

Z = Ц_ах_а + Ц_бх_б + Ц_вх_в – C

немесе

Z = 750(2 - х_а/500) х_а + 1000 (2,5 - х_б/500) х_б + 1500 (1,5 - х_в/500) х_в –

– (200х_а + 600х_б + 400х_в - 100х_ах_б -50х_бх_в+ 150х_ах_в)

Біраз түрлендіргеннен кейін, мақсат функция мына қалыпқа келеді:

Z = 1300х_а + 1900х_б + 1850х_в – 1,5 (х_а)²– 2 (х_б)²– 3 (х_в)² +100х_ах_б +

+ 50х_бх_в – 150х_ах_в → max.

Көріп отырмыз, мақсат функция сызықты емес. Келесі кезекте шектеулер модельдерін тұрғызайық. Есепте жалғыз ғана «Үлкен» шектеу, ол – шығарылатын бұйымдардың жалпы мөл-шерінің шектеуі: х_а + х_б + х_в≤ 500 және мәндері ізделініп отырған айнымалылардың теріс болмау шарты: х_а ≥0, х_б ≥0және х_в ≥ 0. Тағы бір айрықша ескеретін жағдай, ондағы ізделініп отырған айнымалылар бүтін сандар. Модель сызықты емес болған жағдайда, бұл қызықты талап.

Сонымен математикалық модель дайын. Оны MS Excel-дің жұмыс бетіне кестелік модельге көшірейік. Біздің құрған кестелік моделіміз 2.19-суретте көрсетілген. Кестелік модельде мақсат функция формуласын енгізген кезде мұқият болғанымыз жөн (суретті қараңыз).

2.19-сурет. Сызықты емес модельдің шешімі

 

Мақсат функцияны есептеу үшін кестелік модельде оның коэффициенттері: «Айнымалылар қасындағылар», «Квадратты айнымалылардың қасындағылар» және «Айнымалылар көбейтінді-лердің қасындағылар» болып, үш топқа бөлінді. Е12 ұяда мақсат функцияның аталған коэффициенттермен формуласы В4:D4 аралықтағы ұяларға, мәндері ізделініп отырған айнымалылар есеп-тегі жалғыз негізгі шектеу 15-ші жолға және Е15 ұяға шектеудің сол жағының формуласы:=СУММПРОИЗВ(В15:D15;$В$4:$D$4) жазылды. Есептің шешімі, яғни 18-ші жолда В18:D18 аралықтағы ұяларда, қанша дана, сәйкесінше А, Б және В бұйымдары шығарылатыны, сол сияқты Е18 ұяда осы бұйымдарды сатқаннан кейін компанияға қанша пайда түсетіні көрсетілуі керектігі қарастырылды (2.19-сурет).

Келесі кезекте шектеулерді Поиск решения-ғаауыстыра-мыз. Осы істерден кейін Поиск решения-ның сұхбаттасу терезесінің қалпы 2.20-суреттегідей болады.

Поиск решения-ның Параметры арқылы келесі сұхбаттасу терезесінде есептің моделі сызықсыз болғандықтан Линейная модель-ден флажокты алып тастаймыз. Айнымалылардың теріс болмау және автоматты масштабтау шарттарын белгілейміз (флажок қойылады). Осы әрекеттерден кейін есеп орындалуға жіберіледі. Есептің шешімі 2.19-суретте көрсетілген.

2.20-сурет. Поиск решения-ның сұхбаттасу терезесі

Есептің оңтайлы шешімінен (х_а=0) компанияға А бұйымын шығарумен айналысу тиімсіз болатынын байқаймыз. Оның есесіне Б бұйымын 255 дана, ал В бұйымын 245 дана шығару компанияға өте тиімді. Өндірістің мұндай жоспары «Димаш» компаниясына 3751375 теңге пайда түсіреді.

Сызықты емес модельдің шешімінің талдау тәсілдеріне келесі тақырыпта тереңірек тоқталамыз. Дегенмен де, сызықты емес модельді Поиск решения сұхбаттасу терезесінің әртүрлі параметрінде және бастапқы мәндерде біраз зерттеп көрейік.

Сызықты емес модельдерге қатысты Поиск решения-ның параметрлері: Сходимость, Оценки, Разности және Метод поиска. Аталған параметрлер қарастырып отырған сызықты емес модельге қалай әсер ететінін зерттейік. Ол үшін оларды белгілі тәсілмен іске қосамыз да, Выполнить батырмасын басып, есепті шешуге жібереміз. Сөйтіп, аталған параметрлер есептің алынған нәтижесіне ешқандай да әсер етпейтінін байқадық. Есепте анықталған айныма-лылардың бастапқы мәндерін өзгертейік. Айталық, х_а≥ 200 болсын. Оны кестелік модельге В4 ұяға енгіземіз де, есепті орындауға жібереміз. Есептің жаңа шешімі 2.21-суретте көрсетілген. Жаңа шешімді 2.19-суретпен салыстырсаңыз, онда біраз өзгерістер бар екенін байқайсыз. Біріншіден, А бұйымын шығарудың бастапқы мәні белгілі болған жағдайда, өндіріс жоспары айтарлықтай өзгеріске ұшыраған. Екіншіден, осы әрекеттен кейін өндіріске А (248 дана) және Б (252 дана) бұйымдарын шығару тиімді болды да, пайда 6831536 теңге, яғни жуықтап алғанда ол екі еседей көбейді. Демек, қарастырылып отырған мысалдың осы өзгерісінен сызықты модельдерге қарағанда сызықты емес модельдерде айрықшылық-тар болатынын байқаймыз. Атап айтсақ, мұндай модельдерде бірнеше оңтайлы шешімдер болуы мүмкін және сіз ондай шешім-дер қаншалықты және оларды қалай табатынын алдын ала айта-алмайсыз. Дегенмен де, барлық айнымалыларға бастапқы әртүрлі мәндер тағайындап, зерттеулер жүргізу арқылы бір дәйекті шешім қабылдауға болатынына да көз жеткіздік. Біздің мысалда айныма-лыларға кезек-кезек алғашқы мән бере отырып, есепті бірнеше рет шешкенімен, осы қарастырылып отырған екі шешімнен басқа мақсат функцияны жақсартатындай шешім таба алмадық. Сондық-тан қарастырылып отырған модельдің басқа оңтайлы шешімі жоқ деп тұжырымдаймыз (бірақ, бұл тұжырым, сөзсіз, дәлелдеуді талап етеді).

Есептің шарты бойынша қалған екі айнымалыларға жоғарғы-дай міндеттеме жүктелінсе, яғни алғашқы модельге бірінші кезек-те: х_б ≥200, екіншісінде: х_в ≥200, қосымша шектеулер енгізіп, есепті қайта-қайта шығарып, алғашқы екі шешімді қайтадан алдық.

 

2.21-сурет. Сызықты емес модельдің жаңа шешімі

Сызықты емес модельдің параметрлерін өзгертіп, әртүрлі шешім нәтижелерін сақтап отыратын болғандықтан, сценария көмегін қолдандық. Ол үшін Поиск решения мен шешім (2.19-сурет) табылғаннан кейін сұхбаттасу терезесінде Результаты поиска решения алынады, осы терезеде Сохранить сценарий батыр-масын іске қосамыз. Сохранение сценария сұхбаттасу терезесі ашылады да, онда сценария аты енгізіледі. Біздің мысалда, ол «1-ші шешім» деп аталды. Осыдан кейін бірінші шешім сценариясы сақталады. Екінші шешімде (2.21-сурет) А бұйымын 200 данадан кем емес (х_а ≥ 200), үшінші шешімде Б бұйымын 200 данадан кем емес (х_б ≥ 200) және төртінші шешімде В бұйымын 200 данадан кем емес (х_в ≥ 200) өндіру керектігі қарастырылды, шешім нәтижелері жоғарыда баяндалған ретпен сақталынды (келесі тақырып, 2.24-сурет).

Инженерлік-техникалық сызықты емес модельдердің жалғыз ғана шешімі барлығын ерекше «белгілер» арқылы анықтауға бола-ды. Мұндай «белгілер» шектеулермен берілген айнымалылардың барлық өзгеретін аймақтарында мақсат функцияның дөңес немесе ойыс екенін анықтауға болатын, оның сыртқы түріне негізделген. Дегенмен де, көп мүшелі функция түріндегі модельдердің мұндай қасиеттерін тексеру арнайы математикалық әдістерді қолануды талап етеді және жеңіл есеп емес.

Сонымен, сызықты емес модельдердің альтернативті шешім-дерінің ішінен ең керекті оңтайлы шешімді іздейтін қазіргі кезде бірнеше математикалық әдістері бар. Олардың көбісі шартсыз оңтайластыру есептерінде қарастырылады.

 

 

2.2.1 Сызықты емес модельдердің шешімін талдау

Сызықты емес модельдер шешімін талдаудың негізгі мәселесі-кейбір жиі кездеспейтін жағдайлардан басқа табылған шешім шындығында оңтайлы, одан артық басқа шешім жоқ деп сендіруге және сенім білдіруге болмайды. Айнымалылардың әр-түрлі бастапқы мәнінде есепті қайта-қайта шешіп, шешім нәтиже-лерін салыстыру арқылы бір шешімге тоқталып, оны альтернативті оңтайлы шешімдердің ішіндегі ең басты оңтайлы деп тұжырым жасау әрекеті де сізді күмәнданудан құтқармайды. Себебі, ықти-малдықтың шамасы өте аз болса да, сізде әлі де болса ең басты оңтайлы шешімді алмағаныңыз туралы сенімсіздік қалды. Өкініш-ке орай, мұндай жағдайда қандай әдіс, әрекеттер қолдану керектігі туралы біз қарастырған әдебиеттердің ешқайсысынан да кездестіре алмадық. Дегенмен де, айнымалылардың әртүрлі бастапқы мәнінде есепті қайта-қайта шешіп, шешім нәтижелерін салыстыру арқылы, яғни мақсат функция максимумге ізделініп отырса бір шешімде алынған оның ең үлкен (мақсат функция минимумге ізделген жағ-дайда, керісінше) мәніне тоқталып, қалған шешімдердің барлығын өшіріп, тағыда айнымалылардың келесі бастапқы басқа мәнінде есепті шешуді жалғастырып, аяғында бір дәйекті нәтижеге жетуге болатынына күмән жоқ.

Сөйтіп, біздің мысалда осындай әрекеттер жасалынып, бір тұжырымға жеттік деп есептейік.

Сызықты емес модельдер шешімін талдауда Поиск реше-ния сызықты модельдер шешімінде алатын есептер сияқты есеп-терді қалыптастырады. Нәтижелер және шекаралар бойынша есептердің сызықтық модельдер шешімдерінде алынатын есептер-ден ешқандай айырмашылықтары болмайды. Тек, орнықтылық есеп сызықты емес модельдер шешімдерінде басқа түрде құры-лады.

2.22–суретте жоғарыда қарастырылған «Димаш» компания-сының сызықты емес моделінің бірінші шешімінің орнықтылық есебі көрсетілген. Келесі кезекте біз осы есеп бойынша шешім нәтижесіне талдау жасап көрейік.

2.22-сурет. Сызықты емес модель үшін орнықтылық бойынша есеп

Орнықтылық бойынша есепте бізге сезімталдықты талдау үшін, Нормированный градиент бағанасындағы Изменяемые ячейки кестесіндегі Множитель Лагранжа бағанасындағы және Ограничения кестесіндегі мәндер қызықты.

· Нормированный градиент –мәні нөлге тең болады, егер оған сәйкес айнымалы өзінің өзгеріс аралығының шеткі шегіне жақын жатса (0 ≤ х_і ≤ а₀немесе а₁ ≤ х_і ≤ а₂).Егер х_і = 0 немесе х_і = а₀, немесе х_і = а_1, немесе х_і = а₂ болса, онда нормированный градиент (нормалдық баға) осы айнымалының өзгерістерінде (модельдің қалған параметрлері өзгеріссіз қалған жағдай-да) мақсат функция мәнінің лезде (кірпік қаққанша) өзгерісінің жылдамдығын көрсетеді.

· Лагранжа көбейткіші – сәйкес шектеудің оң жақтағы мәнінің өзгерістерінде (модельдің қалған параметрлері өзгеріссіз қалған жағдайда) мақсат функ-ция мәнінің лезде (кірпік қаққанша) өзгерісінің жылдам-дығын көрсетеді. Лагранжа көбейткіші оңтайлы шешімде оған сәйкес шектеу байланысты болса, тек сонда ғана нөлден басқаша.

Қарастырылып отырған екі көрсеткіштің қызметтері, оларға ұқсас сызықтық модельдің нормальдық баға (қосымша қосалқы айнымалы) және көлеңкелік құн (қосалқы баға) көрсеткіштерінің қызметтерімен бірдей емес. Нормированный градиент – оған сәй-кес айнымалы бойынша және Лагранжа көбейткіші – оған сәйкес шектеудің оң жағы бойынша мақсат функциядан алынған туынды-лар (мақсат функция мәнінің лезде (кірпік қаққанша) өзгерісінің жылдамдығы деп аталуының өзі осы себепті және осы құбылыс-тың анықтамасы). Сондықтан, егер нөлдік айнымалы мәнін жоға-рылатқанда, мақсат функция мәні осыншама төмендетілсе, бұл көрсеткіштерді бағалау көрсеткіштері ретінде қолдануға болады.

Сөйтіп, сызықты емес модельдің орнықтылық есебі, оның басқа есептері сияқты, шектеулердің оң жақтарынан басқа, модель-дің параметрлері туралы ештеңе де айтпайды. Сондықтан, егер модельдің басқа параметрлері арқылы оның сезімталдығын зерттеу керек болса, онда модельді керекті параметрлердің мәнінде бірне-ше рет шешуге тура келеді. Төменде осындай шешімдер нәтижесіне талдаулар жүргізіледі.

Екі шешімнің нәтижелерін жоғарыда қысқаша талқыладық. Екінші шешімде пайда 6831536 теңге, яғни біріншіге (3751375 теңге) қарағанда пайда жуықтап алғанда екі еседей көбейді. Мін-детті түрде айнымалылардың біреуі оңтайлы шешімде нөлге тең болуы, екі шешімде де бірдей және бұл осы шешімдердің кемшілігі. Бірінші шешімде, егер оңтайлы шешімге х_а бір бірлігін енгізетін болсақ, онда мақсат функция мәні 23,08 мың теңгеге (бұл 2.22-суретте нормированный градиент-тің мәні) кішірейген болар еді. Осыған сәйкес, екінші шешімде, егер оңтайлы шешімге х_в бір бір-лігін енгізсек, онда мақсат функция мәні 48,536 мың теңгеге (бұл 2.23-суретте нормированный градиент-тің мәні) төмендейді. Сондықтан, егер оңтайлы шешімге енбеген әрбір бұйым 100 дана-дан кем өндірілмесін деген өндірістік қосымша талап қойылса, онда бірінші шешімде пайда 2308 мың теңгеге төмендейді (қалған пайда 943375 теңге құрайды), ал екінші шешімде пайда 4853,6 мың теңгеге төмендейді (қалған пайда 5977936 теңге құрайды). Сөзсіз, мұндай жаңа шектеулерде есепті қайта шығарған жөн. Дегенмен де, қарастырылып отырған шартта да екінші шешімнің айырмашы-лығы анағұрлым жоғары екені анық байқалады.

2.23-сурет. 2-ші шешімде алынған орнықтылық бойынша есеп

Енді шектеулерге көшейік. Біздің модельде шектеу біреу - ол өндірілетін бұйымдардың шектік саны (яғни шектеудің оң жағы бүтін сан өлшем бірлігімен «дана» деп өлшенеді). Сондықтан, осы шектеуге байланысты Лагранжа көбейткіші қор (яғни өндірілген бұйымдардың жалпы саны) бағасы ретінде қарастырылады. Басқа сөзбен айтқанда, Лагранжа көбейткішін барлық бұйымдарды бірге қарастырғанда (біріктірген) бір бұйымнан алынатын пайда (пайда-ға бір бұйым үлесі) немесе жалпы барлық бұйымдар санының (түрлеріне байланыссыз) бір данасына шаққандағы орташа пайда деп түсіндіріледі. Аталған пайдаға бір бұйым үлесі мәнітек алын-ған шешімнің жанында кішкене аймақта сенімді, бірақ, барлық ше-шімі бола алатын аймақта бұл мән сенімді емес екенін ұмытпаған жөн.

Бірінші шешімде Лагранжа көбейткіші 13130 теңгеге, ал екіншіде – 25724 теңгеге тең. Егер өндіріс орны қойылған шарт бойынша өндірілетін барлық бұйымдар саны 500 дананың орнына 501 дана өндіретін болса, онда осыншама шамаға пайда мәні көтерілген болар еді. Көріп отырмыз, бұл жолы бірінші шешімге қарағанда тағыда екінші шешім ұтымды.

Осымен сезімталдықты талдауды бітірсе де болады. Өйткені, орнықтылық есебінде тағы да қарастыратындай ешқандай да мәлімет таба алмадық. Дегенмен де, осы жерде заңды сұрақ туады: «Барлық бұйымдар міндетті түрде өндірілетін болса, онда оларды қаншадан өндірген тиімді болар еді?» Осы сұраққа жауап беру үшін барлық бұйымдар түрлерін 150, 160 және 165 данадан кем емес өндірілуі міндеттелген жағдайда жаңа шектеулер құрылып (х_а≥ 150; 160; 165, х_б≥150; 160; 165 және х_в≥150; 160; 165), есептің қайта-қайта шешімін тауып, нәтижесі жоғарыда баяндалған тәсілмен сценарияда сақталды (2.24-сурет. 5-ші, 6-шы және 7-ші шешімдер).

Сценария кестесінен (2.24-сурет) көріп отырмыз, барлық шешімдердің нәтижелері екінші шешімге жетпейді. Сондықтан, жоғарыда келтірілген сұраққа жалғыз ғана жауап – өндірістің максималды мүмкінділігі В бұйымын қанша өндіру керектігіне байланысты. Егер оны аз өндіру міндеттелінсе, онда өндіріс пайда-сы екінші шешімнің нәтижесіне ұмтылады да, оны көп өндірген сайын пайда төмендейді.

 

2.24-сурет.Сызықты емес модельдің сценариялар бойынша есебі

 

«Димаш» компаниясы өндірісінің сызықты емес модель-дерінің шешімдерін қысқаша талдауды қорытындылайық.

1. Табылған пайда мәні бойынша өндіріске ең тиімді жоспар екінші шешімнің нәтижесінде, мақсат функцияның мына мәнінде Z = 6831536 теңге (сценариядағы 2-ші шешім) алынған: х_а = 248,

х_б =252 және х_в= 0 көрсеткіштер. В бұйымын өндіруді ұлғайтсақ, онда оның бір данасына шаққанда мақсат функция мәні 48,536 мың теңгеге қысқарады. Жалпы өндірілген бұйымдар көлемі ұлғайған сайын пайда да көбейеді, 500 данадан асқан бұйымдар санының бір бірлігінен пайда 25724 теңгеге өседі.

2. Егер өндіріске кез келген бұйымды 150 данадан кем өндірмеу керек деген міндеттеме жүктелсе, онда сызықты емес модель мақсат функцияның мына мәнінде Z = 1796250 теңге, мынадай шешім х_а =150, х_б =200 және х_в= 150 береді. Өндіріске қойылған міндеттемеге байланысты бұл ең оңтайлы жоспар болып есептелінеді. Көріп отырмыз, мұндай жоспарда екінші шешім жос-парына қарағанда пайда төрт еседей кеміген. Кез келген бұйымды өндіру көлемі туралы модельге жүктелетін міндеттеме азайған сайын В бұйымының саны міндеттемеде көрсетілген мәннен аспайды да, ал басқа бұйымдардың саны және мақсат функция мәні керісінше көбейеді. Осыдан, В бұйымды өндіруді максималды қысқартсақ, пайда соғұрлым өседі деген тұжырым өз-өзінен туындайды.

Сонымен, сызықты емес модельдің шешімін талдау қортын-дысы осындай.

 

3. Транспорттық типтес модельдер

3.1 Транспорттық модельдердің жалпы құрамы

Транспорттық есеп - сызықтық программалау есебінің тәжі-рибеде ең көп тарағандарының бірі. Кейде оны тасымалдау есебі деп те айтады. Тек жүкті тасу қарастырылған есеп болған жағдайда есепті осылай атау орынды да. Оның негізгі мақсаты тауарларды тиімді және ұтымды тасымалдау жоспарын құру болса, тәжірибеде осы есептің математикалық аппараттарына және шығару алгоритм-деріне сәйкес келетін жүк тасмалдаудан басқа мақсаттағы есептер-дің түрлері көптеп кездеседі. Сондықтан, мұндай есептер халық шаруашылығында маңызды есептердің қатарына жатады және ол-ардың барлығын транспорттық типтес есептер деп атайды.

Транспорттық есептердің тәжірибелік маңызын терең қарас-тырмастан бұрын қарапайым есептердің алғашқы қойылуын және есепті формалдау ретін талқылайық. Бірінші кезекте транспорттық есептердің жалпы математикалық моделін жазу үшін төмендегідей шартты белгілерді және атауларды қабылдайық.

Жалпы бір тектес өндірілген (шығарылған) өнімді, бір тектес жүк деп, өнім өндіретін орындарды жүк жіберетін пункттер, ал өнім қабылдайтын орындарды тұтынушы пункттер деп атайық. Негізінде мұндай атаулар жуықтап алынған және шартты түрде есептің қойылу мағынасы түсінікті болу үшін қабылданған. Өйткені тәжірибеде халық шаруашылығында, оның ішінде ауыл шаруа-шылығында транспорттық есептің математикалық аппаратын қол-дануға болатын, бірақ мағынасы тіптен ұқсамайтын есептер көптеп кездеседі.

Айталық, жүк жіберетін пункттердің санын - m (олардың нөмірлер индексін j-десек, онда j =1,2,... m), ал тұтынушылардың санын - n (олардың нөмірлер индексін і-десек, онда і=1,2,... n) деп белгілейік.

Әрбір жүк жіберетін пункттерді нөмірлеріне сәйкес (A₁, A₂,...A_m), ал тұтынушыларды нөмірлеріне сәйкес (B₁, B₂,...B_n) деп атайық. Жүк жіберетін пункттерде өндірілген өнімдер көлемі (а₁, а₂, ...а_m) және олардың тұтынушыларға керекті мөлшері (b₁, b₂, ...b_n) жүк көлемдеріндей болсын.

C_іj– і-ші тұтынушыға j-ші жүк жіберетін пункттен жүкті тасығанда, оның бір өлшем бірлігіне есептеген шығын (мұндағы і=1,2,...n; j =1,2,...m), яғни С₁₁, С₁₂, ...С_nm. Бұл көрсеткіш әртүрлі мағынада болуы мүмкін: ақша шығыны, уақыт, еңбек өнімділігі, арақашықтығы және т.б.с.с. Әдебиеттерде бұл көрсет-кішті тасымалдаудың ²Тарифі² немесе кестеге жазылғаннан кейін і-ші жолмен j-ші бағананың қиылысында тұрған тордың бағасы деп атайды.

х_іj - і-ші тұтынушыға j-ші жүк жіберетін пункттен таситын жүктің оңтайлы мөлшері, яғни таситын жүк көлемі белгісіз (х₁₁, х₁₂, ...х_nm ).

Тұрғызылатын математикалық модельдің мағынасы түсінікті болу үшін көмекші кесте тұрғызайық (3.1-кесте).

3.1-кесте

№1	A1	A2	…	Am	Жүкке сұран.
B1	х11 С11	х12 С12	…	х1m С1m	b1
B2	х21 С21	х22 С22	…	х2m С2m	b2
. . .	. . .	. . .	. . .	. . .	. . .
Bn	хn1 Сn1	хn2 Сn2	…	хnm Сnm	bn
Жүк мөлшері	a1	a2	…	am	–

 

Есептің мақсаты әрбір жүк жіберетін пункттен барлық тұ-тынушыларға тиісті мөлшерде жүкті аз шығынмен тасымалдау жоспарын құру, олай болса барлық шығын:

Z=C₁₁х₁₁ +C₁₂х₁₂+...+ C_nmх_nm → mіn (3.1)

Мына жағдайда:

а) барлық жүк жіберетін пункттерден тасымалдауға арналған жүк көлемдері толығымен тиісті орындарына жеткізілінеді, олай болса:

х₁₁ + х₂₁+...+ х_n1 = a₁

х₁₂ + х₂₂ +...+х_n2= a₂

... ... ...

х_1m + х_2m +...+х_nm= a_m (3.2)

б) жүк әрбір тұтынушыға керекті мөлшерде тасылуы керек:

х₁₁ + х₁₂ + ...+ х_1m = b₁ х₂₁ + х₂₂ + ...+ х_2m = b_{2 . . . . . . . . .}

х_n1 + х_n2 + ...+ х_nm = b_n (3.3)

в) әрбір жүк жіберетін пункттен әр тұтынушыға таситын жүктің мөлшері теріс сан болуы мүмкін емес (яғни х_іj>0 - жүк тасу тиімді немесе х_іj=0 - жүк тасу тиімсіз):

х₁₁ ³ 0, х₁₂ ³ 0,... х_nm ³ 0. (3.4)

Сонымен (3.1) ... (3.4) жалпы транспорттық есептің кеңейтіл-ген моделі болып есептелінеді.

- сома белгісі арқылы транспорттық есептің математи-калық моделін құрама түрінде көрсетейік:

(3.5)

Шектеу шарттары:

(3.6)

(3.7)

х_іj≥0, (3.8)

Мына жағдайда:

(3.9)

яғни барлық жүк жіберілетін пункттерде өндірілген немесе жинал-ған жүктің көлемі толығымен тұтынушылардың сұраныстарын қамтамасыздандырады. Мұндай транспорттық есеп жабық немесе балансталған деп аталады.

Егер математикалық модельде 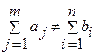шарты орындалмаса, мұндай транспорттық (тасымалдау) есептерінің моделін ашық немесе балансталмаған модель деп атайды.

Транспорттық есептің моделі ашық болған жағдайда есепті шешу үшін оны жабық транспорттық есепке айналдырады.

Егер болса, онда жүк артық жиналған, мұндай жағдайда есепті жабу үшін жалған тұтынушы (B_n+1) енгізіледі де, оның жүкке сұраныс мөлшерін мына қатынаспен есептейді:

b_n+1=Σa_j – Σb_і.

Кейбір әдебиеттерде мұндай есептер «Артығымен тасымал-дау есебі» немесе «Балансталмаған, ашық транспортық есеп» делінеді.

Егер болса, онда өндірілген өнім (жүк) мөлшері тұтынушылардың сұраныс мөлшерін толығымен қамтамасыз ет-пейді, мұндай жағдайда есепті жабу үшін жалған жүк жіберуші пункт (А_m+1) енгізіледі де, ондағы жиналған жүк мөлшерін мына қатынаспен есептейді:

а_m+1=Σb_і–Σa_j.

Жүктің бір бірлігін тасуға кететін шығын (жалған тордың бағасы), яғни бірінші жағдайда: C_n+1,1= 0, C_n+1,2= 0,...,С_n+1,m= 0, ал екінші жағдайда: C_1,m+1 = 0, C_2,n+1= 0,...,С_n,m+1= 0-деп алынады.

Қарастырылып отырған тақырыпта жоғарыдағы келтірілген транспорттық есептердің математикалық модельдері аграрлық өн-еркәсіп кешенінің көптеген есептерінің математикалық аппарат-тарының негізін құрайтынын атап өттік. Мысалға, ауыл шаруа-шылығында ауыспалы егістік жерлерді оңтайлы жоспарлауда, техниканы әртүрлі жұмысқа оңтайлы бөлуде, өндіріс мамандарын әртүрлі жұмысқа тиімді бекітуде, өндіріс орындарын тиімді түрде орналастыруда, тағы басқа да көптеген есептерде қолданылады.

 

3.2 Транспорттық модельдерді шешу әдістеріне

қысқаша шолу

 

Жалпы транспорттық есеп сызықты программалау есебінің құрамына енеді. Дегенмен де, сызықты программалау есептерін ше-шуге арналған компьютерлік программалар пакеттері дамығанға дейін, транспорттық есепті симплекстік әдіспен шешуде, қосымша іс-әрекеттер жүргізуді қажет ететін біраз ерекшеліктер кездеседі. Жоғарыда қарастырылған сызықты программалау есептерінің математикалық моделінде белгісіз х-тер тек бір ғана j = 1,2,...n индекспен берілген. Ал тасымалдау (транспорттық) есебінде белгі-сіздер екі индекспен анықталады.

Транспорттық есепті симплекс әдісімен шешкен кезде екі индексті (өлшемді) көрсеткіштер бір индексті көрсеткіштерге ауыстырылады, мысалы:

х₁₁= у₁, х₁₂= у₂, х₁₃= у₃, х₁₄= у₄, х₂₁= у₅, х₂₂= у₆, және т.б.с.с.

с₁₁= v₁, c₁₂= v₂, c₁₃= v₃, c₁₄= v₄, c₂₁= v₅, c₂₂= v₆, және т.б.с.с.

Осы әрекеттердің нәтижесінде транспорттық есептің матема-тикалық моделі жоғарыдағы баяндалған сызықтық программалау есебінің симплекс әдісімен шығарылатын түріне ауысады. Сөйтіп, есепті шығару үшін симплекс әдісін қолдануға болады. Бірақ, есеп-тің шарты қарапайым, ал ізделінетін белгісіздер өте көп және есепті ешқандай есептеу техникасынсыз қолмен симплекс әдісін қолда-нып шығару өте ыңғайсыз.

Осы келтірілген жағдайларға байланысты ғалымдар транс-порттық есепті шығарудың симплекс әдісінен басқа жолын қарас-тырды. Қазіргі кезде транспорттық есептерді шығаруға өте ыңғай-лы көптеген әдістер жасалынған. Мысалға, үлестіру (тарату) әдісі, Венгер әдісі, потенциал әдісі, Вогель (Фогель) әдісі және тағы басқа әдістер тәжірибеде кеңінен таралған. Солардың ішінен 1949 жылы Кеңестер Одағының белгілі математигі, академик Л.В. Кантарович және М.К. Гавурин ұсынған тарату (үлестіру) әдісі тәжірибеде кеңінен қолданылады.

Транспорттық есептерді шешуге арналған әдістердің көпші-лігі осы есептердің математикалық моделінің мына қасиеттеріне сүйенеді:

– барлық шектеуші шарттар тек теңдік түрінде беріледі;

– әрбір белгісіз тек екі-ақ теңдеудің құрамына енеді;

– шектеуші шарттардағы белгісіздердің коэффициенттері бірге тең.

Транспорттық есептерді шешуге арналған барлық әдістерді қолданғанда есепті шешу әрқашанда тірек жоспарын құрудан басталады (бірінші құрылған кестені базистік шешім деп атайды). Математикалық программалау пәніне арналған әдебиеттерде [12, 13, 15, 16...] тірек жоспарын құрудың бірнеше тәсілдерін кездестіруге болады. Солардың ішінде ең көп кездесетіндері:

n солтүстік - батыс бұрышы ережесі;

n екі есе ұтымды ережесі;

n жол немесе бағана бойынша ең кіші элемент ережесі;

n матрица кестесіндегі ең кіші элемент ережесі;

n Вогель (Фогель) әдісі.

Осы ережелердің бірімен тірек жоспарын құрғанда әрқашан-да толтырылған торлардың саны мына талапқа дәл болуға тиіс:

K_т = m + n –1,

бұл жағдай үлестіру әдісінің бірінші талабы.

Үлестіру (тарату) әдісі. Транспорттық есепті шешуге арнал-ған және тірек жоспарын біртіндеп жақсарту ретін нақтылы көрсе-тіп бейнелейтін ең бірінші жасалған әдіс. Ол осы әдістің негізінде жасалынған МОДИ әдісін (модификацияланған) оқып үйренуге жақсы кіріспе болып табылады.

Бірінші кезекте жоғарыда көрсетілген ережелердің бірімен тірек жоспары құрылады. Барлық бос торлар үшінарнайы тәртіп-пен және ереже бойынша тұйықциклдар тұрғызылады [12].

Бос торлардың сипаттамалары мына формуламен есептелі-неді:

мұндағы – циклдың тақ торларының бағалары (бос тор бірінші тақ тор болып есептелінеді де, әрі қарай жұп, келесісі тақ болып әрі қарай цикл бойынша қайталана береді. Есептеу кез келген бағытта немесе цикл бағытымен жүргізіледі);

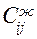– циклдың жұп торларының бағалары.

Оңтайлы жағдайдың белгісін тексеру. Егер Z ® mіn, онда барлық бос торлардың сипаттамасы оң сан болса, яғни: , базистік шешім оңтайлы делінеді. Егер Z ® max, онда барлық бос торлардың сипаттамасы теріс сан болса, яғни: 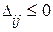, базистік шешім оңтайлы делінеді.

Егер құрылған жоспар оңтайлы емес және бірнеше теріс сипаттама болса, онда осы сипаттамалардың ең кішісі бойынша цикл құрылады да, түрлендіру жүргізіледі, яғни бір рет орнын ауыстыру әрекеті жасалынады [12, 13, 15].

МОДИ әдісі (потенциалдар әдісі).Үлкен өлшемді кестелерде транспорттық есептерді үлестіру (тарату) әдісімен циклдер құрып сипаттамаларды есептеу, өте ыңғайсыз. Осындай есептерді моди-фикацияланған тарату әдісімен (МОДИ) шешкенде есептеу технологиясы көп жеңілденеді. Цикл құрмай-ақ бос торлардың сипаттамаларын мынадай формуламен есептеуге болады:

D_іj = C_іj – (U_і + V_j ),

мұндағы C_іj – бос торлардың бағасы;

U_і– кестенің і-жолының потенциалы;

V_j– кестенің j – бағанасының потенциалы.

Негізінде МОДИ әдісі үлестіру (тарату) әдісімен сәйкес, ал потенциалдар әдісінен айырмашылығы бос тордың сипаттамасын анықтайтын формуланың таңбасы әртүрлі.

Потенциал деп мына формуламен: C_іj^т = U_і+V_j немесе кейбір әдебиеттерде C_іj^т =α_і+β_j есептелген кез келген сандар жұйелерін айтады. Мұндағы С_іj^т – толтырылған (базистік) тордың бағасы; U_і сияқты α_і - кестенің і-жолының потенциалы; V_j сияқты β_j – кестенің j – бағанасының потенциалы.

МОДИ әдісі бойынша бірінші кезектеалғашқы тіректік шешім жоғарыдағы айтылған ережелердің бірімен құрылғаннан кейін жоғарыда келтірілген формула (C_іj^т =U_і+V_j) бойынша базистік (толтырылған) тордың жолының-U_і және бағанасының-V_j потен-циалдары анықталынады. Бірінші жолдың потенциалы U₁ = 0-ге тең деп алынады. Бос торлардың сипаттамаларын мына формула-мен есептейді: D_іj = C_іj – (U_і + V_j ). Келесі жасалатын әрекеттер үлестіру (тарату) әдісімен бірдей.

Дифференциалдық ренталар әдісі. Егер потенциалдар әдісі-мен транспорттық есептің оңтайлы жоспарын анықтау үшін ең бірінші оның тірек жоспарын құрып, одан кейін ол біртіндеп жақ-сартылса, ал дифференциалдық ренталар әдісімен ең бірінші тасымалданатын жүктің негізгі бөлігі ең тиімді түрде бөлінеді де (мұндай әрекет шартты-оңтайлы бөлу делінеді), осыдан кейін келесі итерацияларда (әрекеттерді қайтадан қайталау) жүктің бө-лінбей қалған бөліктері біртіндеп бөлініп, аяғында тиімді оңтайлы жоспар құрылады.

Венгер әдісі.Бұл әдістің негізгі идеясы: жол (бағана) бірдей шамаға d_j (d_і) өзгергенде (көбейсе немесе кемісе) есептің оңтайлы жағдайы ешқандай өзгеріске ұшырамайды.

Қазіргі кезде тірек жоспарын құрғанда бірден немесе оңтайлы шешімге өте жақын базистік шешімді құруға мүмкіндік беретін бірнеше әдістер белгілі. Солардың бірі аппроксимация (аппроксимация ағылшын сөзі – түзету, жақындасу деген ұғымды білдіреді) әдісі немесе оны У. Фогель (Вогель) әдісі деп атайды. Себебі аталған әдістің авторы американдық математик У. Фогель (кейбір ағылшын тілінен аударған оқу құралдарында У. Вогель деп аталынып жүр). Ол экономикалық тұрғыдан қарағанда осы әдіс-тердің ішіндегі ең ұтымдысы.

Сонымен, транспортық және осы типтес есептерді қолмен, компьютерсіз шығаруға арналған бірнеше әдістер мен тәсілдер бар. Олардың бір-бірінен айырмашылығы онша көп емес. Бірақ, көп өлшемді есептерді жедел, тез арада шешімін табуға қазіргі кезде жоғарыдағы аталған әдістер мен тәсілдер жарамсыз. Сондықтан осындай есептерді компьютер көмегімен шығару келешекте қызық-ты болмақ.

Қазіргі кезде нарық жүйесінде тек жүкті тасымалдаумен ай-налысатын транспорттық есептен басқа осы есепке ұқсас модельдер көптеп кездесетіні туралы жоғарыда біренеше рет аталды.

Нарық жүйесінің көптеген есептерінің модельдерін транс-порттық есептердің модельдеріне ұқсатып құрып, оларды осы есептердің әдістерімен компьютерде MS Excel-дің Поиск решения құралының көмегімен шығаруға болатынына келесі тақырыптарда көздеріңіз жетеді.

 

 

3.3 Транспорттық модельдерді компьютерде

шешу тәсілдері

Бір транспорттық есеп құрып, осы мысалды MS Excel - де есепті шешуге арналған барлық нұсқаларды қарастырамыз.

Алматы қаласында орналасқан «Курерьтранс» компаниясы қалаға сырттан келген жүктерді алдын-ала үш қоймада: 1-шіде 1000 дана, 2-шіде 3000 дана және 3-шіде – 2500 дана контейнерлерде сақтайды. Осы жүктерді нарыққа шығаратын төрт (П1, П2, П3 және П4) орындарға жеткізу керек. Айталық, олармен алдын ала жасалған келісім-шарт бойынша сәйкесінше 1-ге – 1300 дана, 2-ге –800 дана, 3-ге – 2700 дана және 4-ге – 1700 дана жеткізу келісілген болсын. Сонымен қатар, жүкті нарыққа шығарушылар-дың (немесе сатып алушылар) қоймалары қаладан әртүрлі қашықтықта орналасқан делік (Ескерту: әрі қарай сатып алушылар делінеді).

«Курерьтранс» компаниясы қоймаларынан жүкті сатып алу-шыларға жеткізуге кететін бір контейнерге шаққандағы шығын алдын ала есептеліп, келесі 3.2-кестеде келтірілген.

3.2-кесте. Бір контейнерге шаққандағы жүкті тасымалдау шығыны, доллармен

Компания қоймалары	Сатып алушылар (нарыққа шығарушылар)
П1	П2	П3	П4
№1
№2
№3

Аталған компанияға жүкті сатып алушылар қоймаларына аз шығынмен жеткізуді қамтамасыздандыратын оңтайлы жоспар құру керек.

Шешуі. Есепті шешудің тәсілдерін қарастырудан бұрын, бірінші кезекте қандай транспорттық есеп қойылғанын тексереміз. Транспорттық есеп ашық не жабық болуы мүмкін, яғни:

1000 + 3000 + 2500 = 1300 + 800 + 2700 + 1700, есеп жабық (балансталған).

Келесі кезекте мына белгісіздерді қабылдаймыз:

х_ij – i-ші компания қоймасынан j-ші сатып алушылардың қоймасына тасылатын жүктің оңтайлы мөлшері (есептің шарты бойынша контейнерлердің оңтайлы саны), i =1,2,3 және j= =1,2,3,4.

Z =50x₁₁ + 150x₁₂ + 60x₁₃ + 75x₁₄ + 100x₂₁ +30x₂₂ + 100x₂₃ + 40x₂₄ + + 70x₃₁ + 180x₃₂ +210x₃₃ + 120x₃₄ → min

Егер есеп жабық болса (балансталған), онда компания қойма-ларындағы барлық жүктер толығымен тасылады. Мұндай жағдайда тасымалданатын жүктерге шектеулер мына түрде жазылады:

x₁₁ + x₁₂ + x₁₃ + x₁₄ = 1000,

x₂₁ + x₂₂ + x₂₃ + x₂₄ = 800,

x₃₁ + x₃₂ + x₃₃ + x₃₄ = 2500.

Барлық сатып алушыларға жүктер керекті мөлшерде жеткі-зілуге тиіс:

x₁₁ + x₂₁ + x₃₁ = 1300,

x₁₂ + x₂₂ + x₃₂ = 800,

x₁₃ + x₂₃ + x₃₃ = 2700,

x₁₄ + x₂₄ + x₃₄ = 1700.

Осыдан кейін есептің математикалық моделін MS Excel-ң жұмыс бетіне жазамыз. MS Excel-ге жазылған кестелік модельдің түрі 3.1-суретте берілген. Кестелік модельдің құрамы өндірістік модель құрамынан өзгеше. Себебі кестелік модельде тасымалдау тарифі матрицасын және оңтайлы мәндері ізделінетін белгісіздер матрицасын жеке-жеке құрған ыңғайлы.

Ескерту:G11:G13 және B15: E15 ұяшықтарда тұрған сан мәндерін форматтау үшін, оларды белгілеп алып, сұхбаттасу терезесіне (⇐ Предыдущая567891011121314Следующая ⇒