 |
|
Тапшысымен тасымалдау есебі 1 страница
Жоғарда транспортық типтес есептердің теориялық жағдай-ын баяндаған бөлімде егер  болса, онда өндірілген өнім мөлшері тұтынушылардың сұраныс мөлшерін толығымен қамтама-сыз етпейді делінді. Мұндай жағдайда есепті «Тапшысымен тасмалдау есебі» немесе «Баланысталмаған, ашық транспортық есеп» деп атайды.
болса, онда өндірілген өнім мөлшері тұтынушылардың сұраныс мөлшерін толығымен қамтама-сыз етпейді делінді. Мұндай жағдайда есепті «Тапшысымен тасмалдау есебі» немесе «Баланысталмаған, ашық транспортық есеп» деп атайды.
Айталық, компанияның №3 қоймасында 2500 дана контей-нерлер емес 2100 дана контейнерлер сақталынуда дейік. Есептің қалған шарттары өзгерусіз қалсын. Мұндай жағдайда «Курерь-транс» компаниясының барлық қоймаларында:
1000 + 3000 + 2100 = 6100 дана.
Сатып алушыларға жүк керек:
1300 + 800 + 2700 + 1700 = 6500 дана.
Сонымен, 6500 дана контейнерлерге тұрған жүкке сұраныс болса, компания қоймаларында бар жоғы 6100 дана контейнерлерде жүктер сақтаулы, яғни ұсыныс тапшы, есеп ашық (баланысталма-ған).
Мұндай есептерде жіберілетін пункттерге шектеулер теңдеу түрінде, ал қабылдайтын пункттерге шектеулер теңсіздік түрінде жазылады. Біздің мысалымызда мынадай шектеулерді аламыз. Тасмалданатын жүктерге шектеулер мына түрде жазылады:
x11 + x12 + x13 + x14 = 1000,
x21 + x22 + x23 + x24 = 800,
x31 + x32 + x33 + x34 = 2100.
Барлық сатып алушыларға жүктер керекті мөлшерде жеткізіл-мейді, яғни:
x11 + x21 + x31 ≤ 1300,
x12 + x22 + x32 ≤ 800,
x13 + x23 + x33 ≤ 2700,
x14 + x24 + x34 ≤ 1700.
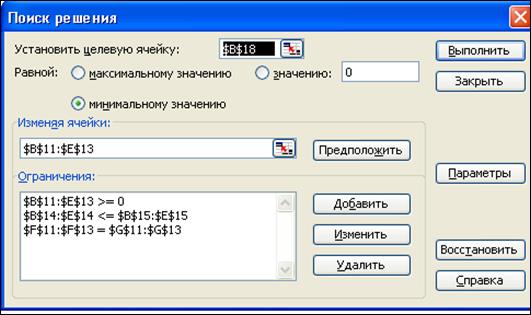
3.7-сурет. Поиск решения сұхбаттасу терезесі баланысталмаған
тапшы есебі үшін

3.8-сурет. Баланысталмаған тапшысымен тасымалдау есебінің шешімі
Қарастырылып отырған математикалық модель үшін кестелік модель баланысталған есептің кестелік моделі формасын тегістей қайталайды. Тек, B15:E15 ұяларын қалыптастырғанда “=”-белгісі “<=”-белгісімен ауыстырылды да, Поиск решения сұхбаттасу терезесінде B14:E14 = B15:E15 шектеулері B14:E14 <= B15:E15 шектеулеріне ауысады (3.7-суретті қараңыз). Табылған шешім 3.8-суретте көрсетілген.
Есептің шешімінің нәтижесі шамамен балансталған жабық транспорттық есептің шешу нәтижесін қайталайды. Тек, мұнда П3 сатыпалушы 400 дана жүктер тиелген контейнерлерді ала-алмайды. Барлық тасымалдау шығыны 437 мың доллар құрайды (мақсат функцияның мәні B18 ұяшықта).

3.9-сурет. Тапшысымен тасмалдау есебінің шешімі
Есепті тағы да бір нұсқада шешу тәсілін қарастырайық. Транспорттық есептің моделі ашық болған жағдайда есепті шешу үшін оны жабық транспорттық есепке айналдыратыны жоғарыда теориялық бөлімде түсіндірілді. Біздің жағдайда, компания қойма-ларындағы жүктер мөлшері тұтынушылардың сұраныс мөлшерін толығымен қамтамасыз етпейді, яғни есеп «Тапшысымен тасмал-дау есебі». Оны жабу үшін жалған жүк жіберуші № 4 қойма енгі-зіледі де, ондағы жиналған жүк мөлшерін мына қатынаспен есеп-тейміз: аm+1=Σbі–Σaj, яғни №4 жалған қоймаға (6500 – 6100 = 400) дана жүк тиелген контейнерлер керек. Жүктің бір бірлігін тасуға кететін шығын (жалған тордың бағасы), яғни C41=0, C42= 0, С43 = 0 және C44 = 0 деп алынады. Енді осы көрсеткіштерді MS Excel кестелік модельге енгізіп, есепті белгілі тәсілмен Поиск решенияқұралымен шығарайық (3.9-сурет). Сонымен, 3.9-суреттен көріп отырмыз тағыда 1-нұсқада алынған нәтижені қайталадық.
Талапты оқырмаға жоғарыда баяндаған тәсілдермен «Арты-ғымен тасымалдау» есебін, өз бетінше MS Excel көмегімен шығаруды ұсынамыз. Жоғарыдағы баяндалған тәсілдерді дұрыс меңгерген жағдайда ешқандай қиындықсыз мақсатыңызға жетесіз.
3.5 Тағайындау туралы есептер
Тәжірибеде дискретті программалау әдістерімен шығарыла-тын есептердің бірі тағайындау есебі. Халық шаруашылығында, оның ішінде агроөнеркәсіп кешенінде тағайындау есебіне ұқсас есептер көптеп кездеседі. Мысалға, ауыл шаруашылығында бір түрлі техникалармен бірнеше түрлі жұмыстар орындалады, бір жұмысшы бірнеше түрлі жұмыс орындай алады, бірақ бір жұмыс-шының немесе бір техника түрінің кез келген жұмыста еңбек өнімділігі (жұмыс өнімділігі) немесе берілген уақыт аралығында жұмыс көлемін орындау қабілеті, ақырында әрбір жұмыста олардың тиімділігі әртүрлі болуы мүмкін. Сондықтан техника түрлерін немесе жұмысшыларды тиімді бөліп, әрбір жұмысқа бекітіп, тағайындау маңызды экономикалық есептердің бірі. Мұндай мағынадағы есептер жалпы "Тағайындау есебі" делінеді.
Айталық n тұрлі жұмысты n жұмысшылар орындай алады делік. Сонымен қатар әрбір жұмысшының кез-келген жұмыстағы еңбек өнімділігі (шығаратын шығыны немесе әкелетін пайдасы немесе т.б.с.с. көрсеткіштерінің бірі) белгілі босын. Оны Cіj деп белгілейік,  және
және 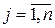 .
.
Есептің экономикалық мәнісі – әрбір жұмысқа тиісті жұмыс-шыны тағайындау нәтижесінде өндіріс орны ең жоғары тиімділікке (максималды еңбек өнімділігіне немесе пайдаға немесе минималды жұмыстың орындалу уақытына) жету керек. Сонымен қатар, бір жұмысшы тек бір жұмысты ғана атқаруға тағайындалуға тиіс.
Есептің математикалық моделін құру үшін Xіj-мен і-жұмыс-кердің j-жұмысын атқаруға тағайындалғанын белгілейік. Егер Xіj=1болса, онда і-жұмыскер j-жұмысқа тағайындалған, керісінше жағдайда, яғни Xіj=0 ол тағайындалмаған. Сонымен, мәндері тек 0 немесе 1 болатын, біз бірінші рет екілік айнымалылармен кездестік. Әдебиеттерде екілік айнымалылар бинарлық, бульдік немесе логикалық деп аталады. Келесі кезекте осындай айнымалылармен қалай жұмыс істейтін жағдайларға тоқталайық. Екілік айнымалы-лар арқылы есептің жалпы математикалық моделін былай жазуға болады:
Мақсат функция
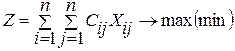 (3.10)
(3.10)
Мына жағдайда
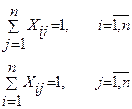 (3.11)
(3.11)
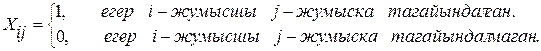
Тағайындау есептеріне айнымалылардың теріс болмау шарты жазылмайды.
Келтірілген модельден «Тағайындау» есебі «Тасымалдау» ес-ебімен өте жақын «Туысқан» екенін байқауға болады. «Туысқан»-дық есептің математикалық құрамында, жұмысшылар және жұмыс түрлері, жүкті жіберу және қабылдау пунктеріне сәйкес келетіні арқылы байқалса, ал айырмашылығы жұмысшылар саны жұмыс түрлерінің санына тең болуы (бірақ, мұндай жағдай тағайындау есебі үшін міндетті шарт емес), сонымен қатар айнымалылардың екілік типте болуы және олардың жолдар және бағаналар бойынша сомасы бірдей бірге тең болуында.
Егер жұмыскерлер санымен жұмыс түрлерінің саны бірдей болса, онда мұндай есептерді баланысталған дейді де, ал керісінше жағдайда баланысталмаған делінді.
Егер кейбір жұмыстар бірнеше жұмыскерлер арқылы орын-далса, бірақ жалпы керекті жұмыскерлер санымен бар жұмысшылар саны тең болса, онда мұндай тағайындау есептері де баланысталған делінеді. Мұндай есептерді «ұжымы» мен жұмыстарды орындау деп те атауға болады. Осындай жағдайларда «тасымалдау» кестесі мына түрде жазылады:
3.3-кесте. «Ұжымы» мен жұмыс орындау жағдайдағы тағайындау
есебінің кестесі
| Жұмысшылар | Жұмыстар түрлері | ∑ Хij | |||
| ... | m | ||||
| х11 С11 | х12 С12 | … | х1m С1m | ||
| х21 С21 | х22 С22 | … | х2n С2m | ||
| … | … | … | … | … | … |
| n | хn1 Сn1 | хn2 Сn2 | … | хnm Сnm | |
| ∑ Хij | K1 | K2 | … | Km |
Есеп балансталған болу үшін мына шарт орындалуға тиіс:
K1+ K2 + …+Km = n.
Жұмысшылар және жұмыс түрлер саны бірдей болғандағы есептің математикалық моделі (3.10) және (3.11) формулалар арқы-лы өрнектелінеді. Ал «ұжымы» мен жұмыстарды орындайтын бол-са, 3.3-кестедегі көрсетілген тәртіп бойынша есептің математи-калық моделіне біраз өзгерістер енгізіледі, яғни:
Мақсат функция
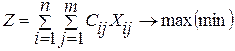 (3.12)
(3.12)
Мына жағдайда
 (3.13)
(3.13)
K1+ K2 + …+Km = n. (3.14)
Баланысталмаған тағайындау есептері.Баланысталмаған тағайындау есептерінде көбінесе жұмыскерлер саны жұмыс түрлері санынан көп болады. Бірақ, мұндай жағдай міндетті шарт емес. Себебі тәжірибеде керісінше жағдайлар да кездесуі мүмкін. Ондай есептер кездескен жағдайда «Артық мөлшерлі есептер үшін шек-теулер» тәсілін оқып-зерделеген оқырман ешқандай қиындықсыз мұндай есептерді өзбетінше талқылай алуға тиіс. Біз тек жұмыс-керлер жұмыс түрлерінен көп болған жағдайды қарастырамыз. Мы-салға, m жұмыс түрлері және n жұмыскерлер, сонымен қатар m < n болсын. Сөзсіз, барлық вакансиялар қолданылып, бірнеше жұмыс-керлер жұмыссыз қалады да мынадай шектеулер құрылады:
– жұмыскерлердің жұмысқа тағайындалу жағдайы (жолдар бойынша сома)
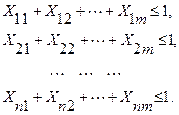
– әрбір жұмыс түрлері толығымен жұмыскерлермен қамта-масыздандырылады (бағаналар бойынша сома)
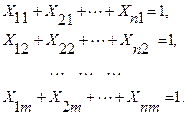
«Ұжымы» мен жұмыстарды орындауға баланысталмаған тағайындау есептерінде шектеулер қалай жазылатын тәсілдерін қарастырайық. Мұндай есептерде мынадай шарт орындалынады: K1+ K2 + …+Km < n. Келтірілген шартты ескере отырып, есептің шектеулерін былай өрнектейміз:
– жұмыскерлердің жұмысқа тағайындалу жағдайы (жолдар бойынша сома)
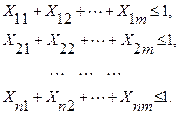
– әрбір жұмыс түрлері толығымен жұмыскерлермен қамта-масыздандырылады (бағаналар бойынша сома)
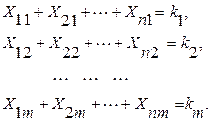
Мұндай есептер комбинаторлық класс есептеріне жатады. Қазіргі кезде осындай есептерді шешуге арналған бірнеше әдістер бар. Солардың ішіндегі ең көп таралғаны Венгер әдісі. «Тағайын-дау» есептерінің барлық варианттарын, n-үлкен сан болған жағдайда, қарастыру мүмкін емес. Себебі бір жұмысшыны барлық жұмысқа тағайындаумен қатар барлық жұмысшы бойынша n!-нұсқаларды қарастыру керек. Сондықтан мұндай есептер қазіргі кезде MS Excel көмегімен шығарылады.
3.5.1 Баланысталған «Тағайындау» есебін MS Excel көмегімен шешу тәсілі
Қарапайым өлшемді бір мысал қарастырайық. «Қуат» атты құрылыс компаниясы 4 құрылыс объектісінде бетон құю жұмысын жүргізбекші. Фирмада осы жұмыспен 4 бригада айналыса алады. Әрбір бригаданың жетекшілері аталған объектілерде болып, жұмыс көлемін және қанша уақытта орындай алатындарын бағалады. Бригада жетекшілерінің мәліметтері 3.4- кестеде келтірілген.
Компания басшысының мақсаты - әрбір объектілерге брига-даларды тағайындай отырып, қарастырылып отырған барлық объектілерде бетон құю жұмыстарын қысқа уақыт аралығында орындауды қамтамасыздандыратын жоспар құру.
Компания басшысына тиімді жоспар құруға көмек көрсе-тейік. (Компания бізге қанша төлейді? Сөзсіз қызықты). Бригадалар және объектілер саны бірдей, сондықтан есеп баланысталған тағайындау есебі.
3.4-кесте
Бригадалардың бетон құю жұмысын орындай алатын мүмкіндіктері, күн
| Бригадалар | Құрылыс объектілері | |||
| №1 | ||||
| №2 | ||||
| №3 | ||||
| №4 |
Шешу. Баланысталған тағайындау есебінің математикалық моделін құрайық. Модельде 16 екілік айнымалыларды Xij( і=1,2,… .,4 және j=1,2,…,4) анықтаймыз. Егер Xij=1 тең болса, онда і – бри-гадасы j - объектіге тағайындалады, және Xij=0 тең болса і – бри-гадасы j - объектіге тағайындалмайды. Барлық объектілерде бетон құю жұмыстарының орындалу уақыттарының сомасы мақсат функ-цияны өрнектейді, яғни:
Z = 30X11 + 40X12 + 50X13 + 60X14 +36X21 + 41X22 + 52X23 + 58X24 +
+ 28X31+44X32+49X33 +57X34 +35X41+39X42 + 49X43 + 63X44 
Шектеулерді жазайық. Есеп баланысталған, сондықтан 4 қарапайым шектеулер теңдік түрінде (матрицалардың жолдар бойынша сомасы):

және 4 шектеулер тағы да теңдік түрінде (матрицалардың бағана-лар бойынша сомасы) беріледі:
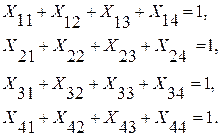
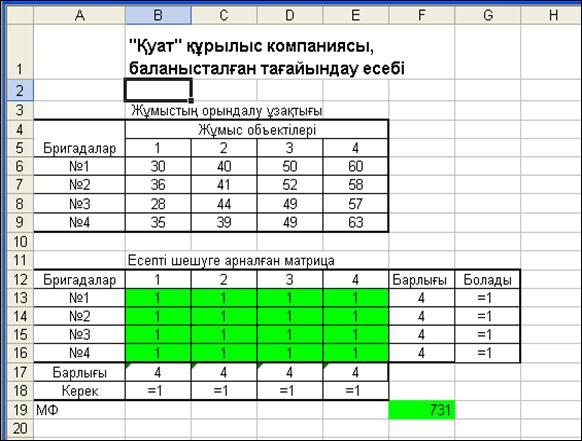
3.10-сурет. Баланысталған тағайындау есебінің кестелік моделі
Есеп бізде баланысталған, сондықтан есепте шектеулер 8 түрлі қарапайым теңдеулерден құралды. Келесі кезекте Excel–дің жұмысшы бетіне құрылған есептің моделі арқылы кестелік модельді тұрғызамыз. Осы жерде Excel жұмыс беті міндетті түрде тиімді жобалану керектігін ерекше атап өтейік. Біздің жоба бойынша кестелік модель 3.10-суретте келтірілді. Ол транспорт есебін Excel –де шешудегі кестелік моделге ұқсас.
Мақсат функция мәні F19 ұясында 3.10-суретте fx жолында келтірілген формула бойынша есептелінді. B17:E17 және F13:F16 аралықтарда алдыңғы бөлімдерде келтіргендей жолдар және бағаналар бойынша айнымалылар сомасы есептелінеді, мысалға, =СУММА(B13:B16) немесе =СУММА(B13:E13), сөйтіп, осындай формулалар матрицаның ақырғы жолына және бағанасына дейін жазылады.
Поиск решения құралын іске қосамыз. Сұхбаттасу тере-зесінде мақсат функцияның адресін F19, бағытын және айныма-лылардың адрестер аралығын көрсетеміз (3.12-сурет). Есептің B13:E16адрес аралығындағы айнымалылардың екілік болу шартын енгіземіз (3.11-сурет).
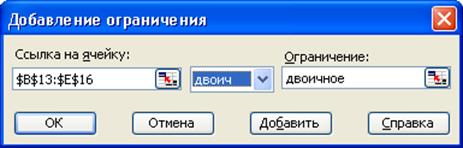
3.11-сурет. Есептің айнымалыларының екілік шарты
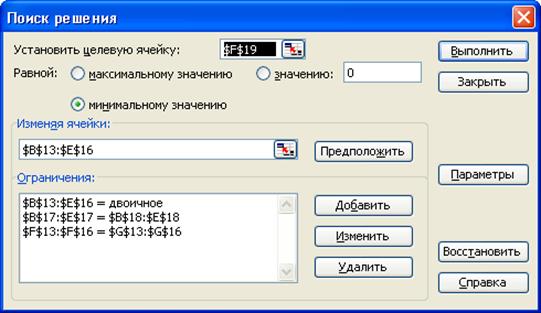
3.12 -сурет. Баланысталған тағайындау есебін шығару үшін
Поиск решения –ның сұхбаттасу терезесі
Барлық шектеулерді енгізгеннен кейінгі Поиск решения–ның сұхбаттасу терезесі 3.12-суретте көрсеткендей түрге енеді. Параметры батырмасын басып, келесі сұхбаттасу терезесінде Линейная модель және Автоматическое масштабирование жазба-ларына белгі қоямыз. Неотрицательные значения жазбасына белгі қоюдың қажеттігі жоқ.
Ақырында, Поиск решения -ның сұхбаттасу терезесінде Выполнить батырмасын шерткеннен кейін, есептің 3.13-суретте көрсеткен шешімін аламыз.
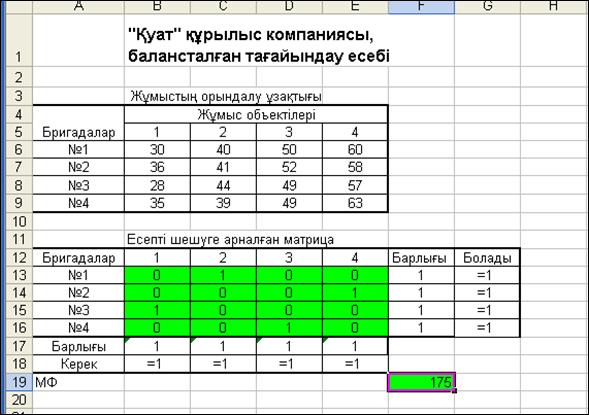
3.13-сурет. Баланысталған тағайындау есебінің шешімі
Ескерту. Егер есепте кем дегенде бір айнымалыға екілік шарты қойылса, онда Поиск решения құралы тек есептің шешу нәтижесін генерациялайды.
Сонымен, есептің шешімінен мынадай қорытындыға тоқтала-мыз: бірінші бригаданы 2-ші объектіге, екінші бригаданы 4-ші объектіге, үшіншіні 1-ші объектіге, ал төртінші бригаданы 3-ші объектіге жібергенде, барлық объектілердегі жұмыстар қысқа мер-зімде орындалады. Барлық жұмыстың орындалу уақытының ұзақ-тығы 175 жұмыс күнін құрайды.
3.5.2 Баланысталмаған «Тағайындау» есебін MS Excel көмегімен шешу тәсілі
«Қуат» құрылыс компаниясы бригадаларды бетон құятын объектілерге тағайындамас бұрын, тағы бір бригада кезекті жұмы-сын бітіріп, бетон құю жұмысқа оларды да тағайындауын өтінді. Бригаданың жетекшісі әрбір объектідегі жұмысты (1-объектіні 29 жұмыс күнінде, 2-шіні 40 күнде, 3-шіні 48 күнде және 4-шіні 59 күнде бітіреміз деп) бағалап, өздерінің шешімдерін компанияға жеткізіп үлгерді. Сонымен, әрбір бригаданың қанша уақытта әрбір объектіде жұмысты орындайтыны 3.5-кестеде келтірлген.
3.5-кесте
| Бригадалар | Құрылыс объектілері | |||
| №1 | ||||
| №2 | ||||
| №3 | ||||
| №4 | ||||
| №5 |
Есепте бригадалар саны объектілер санынан көп, сондықтан балансталмаған тағайындау есебі құрылды.
Шешу. Баланысталмаған тағайындау есебінің математикалық моделін құрайық. 20 екілік айнымалыларды Xij ( і=1,2,…,5 және j=1,2,…,4) анықтаймыз. Егер Xij =1 тең болса, онда і - бригадасы j - объектіге тағайындалады, және Xij =0 тең болса і - бригадасы j - объектіге тағайындалмайды. Барлық объектілерде бетон құю жұ-мыстарының орындалу уақыттарының сомасы мақсат функцияны өрнектейді, яғни:
Z = 30X11 + 40X12 + 50X13 + 60X14 +36X21 + 41X22 + 52X23 + 58X24 +
+ 28X31 + 44X32 +49X33 +57X34 +35X41+39X42 + 49X43 + 63X44 +
+ 29 Х51 + 40Х52 + 48Х53 + 59 Х54 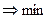
Шектеулерді жазайық. Есеп баланысталмаған, сондықтан 4 қарапайым шектеулер теңдік түрінде (матрицалардың бағаналар бойынша сомасы):
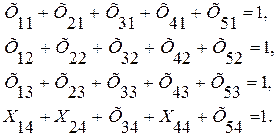
және 5 шектеулер теңсіздік түрінде (матрицалардың жолдар бойынша сомасы) беріледі:
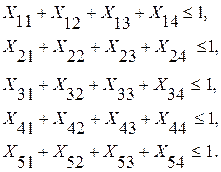
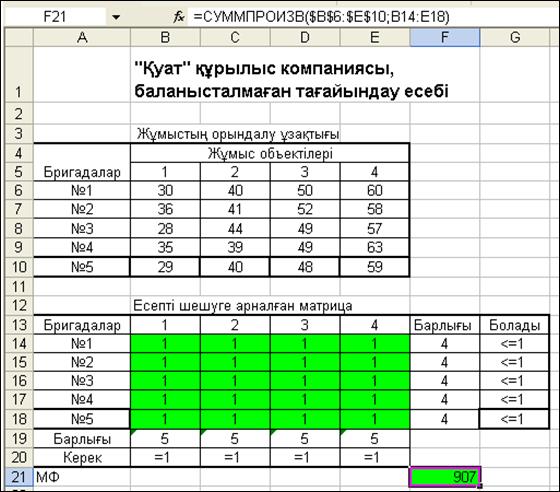
3.14 – сурет. Баланысталмаған тағайындау есебінің кестелік моделі
Есептің кестелік моделі (3.14-сурет) баланысталған тағайындау есебінің кестелік моделіне өте ұқсас (3.1-суретті қараңыз). Тек есепке 5-ші бригаданың мәліметтері қосылғанда, ал G13:G17 ұялары қалыптасқан да, “=” белгісінің орнына “<=” белгісі қойылған.
Есепті шешу үшін Поиск решения-ның сұхбаттасу терезесі мынадай түрде болуға тиіс (3.15-сурет). Бұл сұхбаттасу терезесі 3.3-суретпен сәйкес, бірақ негізгі өзгешелігі айнымалылар аралықта-рының адересі өзгерді және F13:F16 = G13:G16 шектеулері F13:F18<= G13:G18 шектеулерімен ауыстырылды.

3.15 - сурет. Баланысталмаған тағайындау есебін шығару үшін
Поиск решения –ның сұхбаттасу терезесі
Поиск решения-ның сұхбаттасу терезесіндегі Выполнить батырмасын шерткеннен кейін есептің 3.16-суретте келтірілген шешімін аламыз.
Алынған шешімнен 1-ші бригада жұмыссыз қалатыны, 2-ші бригада 4-ші объектіге, 3-ші бригада 1-ші объектіге, 4-ші бригада 2-ші объектіге, ал 5-ші бригада 3-ші объектіге жіберілетіні байқала-ды. Сөйтіп, барлық жұмыстың орындалу уақытының ұзақтығы 173 жұмыс күннен тұратынын, оның баланысталған есептен 2 күн қысқа екенін анықтадық.
Сонымен жоғарыда, тәжірибеде көп кездесетін классикалық транспорттық типтес модельдердің MS Excel-де шешу тәсілдері қарастырылды. Бірақ, өндірісте кейбір жағдайларда транспорттық типтес модельдерге көптеген өзгерістер енгізуге тура келеді. Тіпті кейде транспорттық типтес модельдің жалпы құрлымы өзгеріп кетуі де мүмкін. Мысалға, кейбір жүк жіберілетін пункттерден жүкті қабылдайтын пункттерге жүкті тасымалдауға рұқсат жоқ немесе өнімді өндіруге және оны тұтынушыға жеткізуге кететін шығындар сомасы минималды болуы қарастырылса және т.б.с.с.
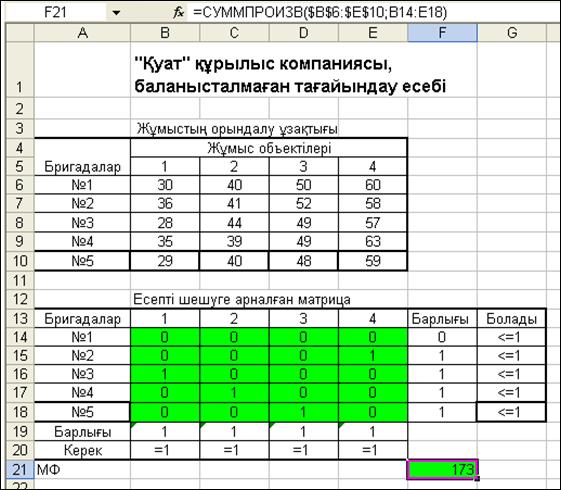
3.16-сурет. Баланысталмаған тағайындау есебінің шешімі
Мұндай жағдайларда транспорттық типтес модельдерді MS Excel-де шешу біраз күрделенеді және оларға арналған арнайы ережелер жоқ, тек есептің мақсатын дұрыс түсініп, адекватты математи-калық модель жазып, және MS Excel-дің жұмыс бетінде ыңғайлы кестелік модель құрсаңыз, табысты шешім алатыныңыз сөзсіз. Ісіңізге сәт, талабыңызға нұр жаусын!
4. Агроөнеркәсіп кешенінің маңызды есептері
4.1 Көпкезеңді жарым-жартылай бүтін санды модель