 |
|
Тапшысымен тасымалдау есебі 6 страница
1-нұсқа. 1Ө1 → 1Ө2 → 1Ө3, яғни барлық өнімдер 1-ші техно-логиялық тәсілмен өндіріледі, сәйкес өнімдердің оңтайлы мөлшер-лері (х11; х12 және х13).
2-нұсқа. 2Ө1 → 1Ө2 → 1Ө3 ↔ (х21; х12 және х13).
3-нұсқа. 3Ө1 → 1Ө2 → 1Ө3 ↔ (х31; х12 және х13).
4-нұсқа. 1Ө1 → 2Ө2 → 1Ө3 ↔ (х11; х22 және х13).
5-нұсқа. 2Ө1 → 2Ө2 → 1Ө3 ↔ (х21; х22 және х13).
6-нұсқа. 3Ө1 → 2Ө2 → 1Ө3 ↔ (х31; х22 және х13).
Құрылған нұсқаларға байланысты есептің математикалық модельдерін тұрғызайық. Есепте, өндіріс орнында өндіруге бола-тын өнімдер түрлерінің саны n=3 және қолданылатын қорлар түрлерінің саны m=4.
Осы жерде оқырманның мынадай жағдайға көңіл аударғаны жөн. Айталық, әрбір нұсқадағы модельді жеке-жеке қарастырып, олардың ішіндегі ең максималды пайдаға жеткен шешім арқылы, өндіріс орнының оңтайлы бағдарламасын құруға болады делік. Бірақ, мұндай жағдайда есепті шешу барысында ұзақ уақыт көп есептеулер жүргізуге және аралық нәтижелерді қайта-қайта экранға шақырып, оларды сақтап отыруға тура келеді. Есептің өлшемі ұлғайған сайын, мұндай тәсілмен есепті шешу қиындай бастайды, тіпті кейде тәжірибелік үлкен өлшемді есепті шешу тиімсіз болуы мүмкін. Есептің нәтижесін құжаттау үшін де аталған тәсіл өте ыңғайсыз. Негізінде өндіріс орнына дұрыс шешім қабылдау үшін есепті шешу нәтижесі бойынша барлық нұсқадағы шешімдерді жан-жақты талдау көзделінеді. Сондықтан, тек пайданың макси-малды мәні арқылы шешім қабылдау кейбір жағдайларда өндіріс талаптарына толық жауап бермеуі мүмкін. Сөйтіп, есепті техноло-гиялық тәсілдердің мүмкін бола алатын бірлестігінен құрылған нұс-қалар бойынша, «қорды оңтайлы бөлу» есебі сияқты жеке-жеке қарастыру бізге қызықты емес. Мұндай қойлымадығы есептерді шығару тәсілдері жоғарығы бөлімдерде жан-жақты баяндалды.
Сонымен, жоғарыда келтірген өндірістік нұсқалар есептің шарты бойынша міндетті түрде бірге қарастырылады. Демек, есеп-тің жалпы математикалық моделі әрбір нұсқа бойынша құрылған экономикалық-математикалық модельдер жинтықтарынан, яғни блоктық матрицадан және оларды біріктіруші блоктан тұруға тиіс (4.9-кесте).
4.9-кесте. Блоктық матрица
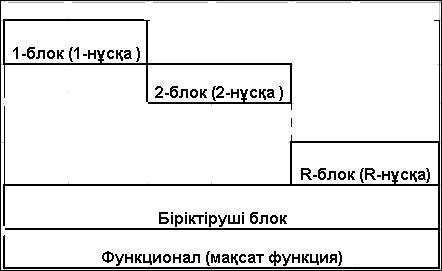
Диагональ бойынша орналасқан тікбұрышты матрицалар блоктарынан құралған кестені блоктық матрица деп атайды. Барлық блоктардың (біздің жағдайда әрбір блок ретінде есептің шарты бойынша құрылған нұсқалар түсініледі) айнымалылары бір жүйеде немесе теңдікте біріктіріледі де осы теңдікті біріктіруші блок деп атайды (4.9-кестені қараңыз).
1-Блок (1-нұсқа) Нұсқаның мақсат функциясының математи-калық моделін (4.19) формула бойынша:
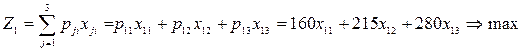
мына жағдайда:
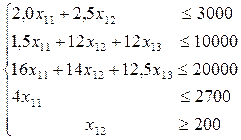
Есептің жалпы моделінде нұсқалардың мақсат функциясы шектеу қатарына жазылады, яғни:
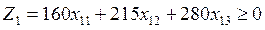 (4.34)
(4.34)
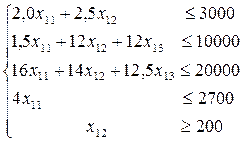 (4.35)
(4.35)
х11 ≥ 0 ; х13 ≥ 0
2-Блок (2-нұсқа).
Мақсат функция:
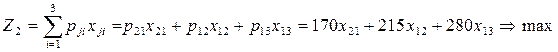
одан:
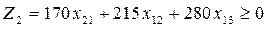 (4.36)
(4.36)
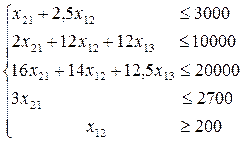 (4.37)
(4.37)
х12 ≥ 0 ; х13 ≥ 0
3-Блок (3-нұсқа).
Мақсат функция:
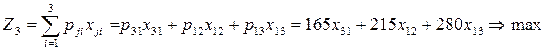
одан:
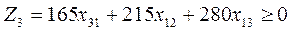 (4.38)
(4.38)
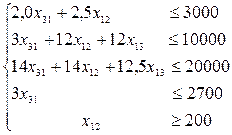 (4.39)
(4.39)
х31 ≥ 0 ; х13 ≥ 0
4-Блок (4-нұсқа).
Мақсат функция:
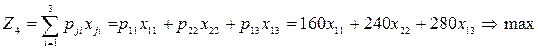
одан:
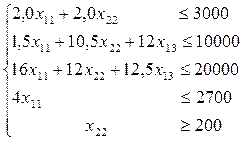 (4.40)
(4.40)
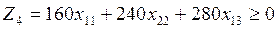 (4.41)
(4.41)
х11 ≥ 0 ; х13 ≥ 0
5-Блок (5-нұсқа).
Мақсат функция:
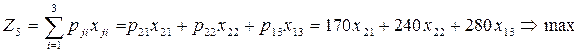 одан:
одан:
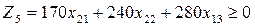 (4.42)
(4.42)
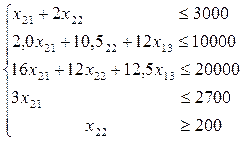 (4.43)
(4.43)
х12 ≥ 0 ; х13 ≥ 0
6-Блок (6-нұсқа).
Мақсат функция:
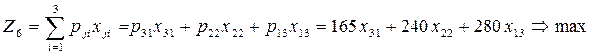 одан:
одан:
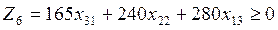 (4.44)
(4.44)
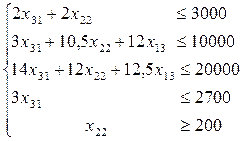 (4.45)
(4.45)
х13 ≥ 0 ; х13 ≥ 0.
Есептің жалпы математикалық моделінде келтірілген (4.27) формула бойынша, технологиялық тәсілдер бірлестіктерінің нұсқа-ларынан алынатын пайдалар сомасы максималды болуға тиіс, яғни:
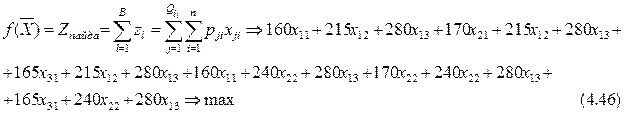 мынадай шектеулерде: (4.34; 4.35;...4.45).
мынадай шектеулерде: (4.34; 4.35;...4.45).
Негізінде (4.46) формула бойынша барлық технологиялық тәсілдер бірлестіктерінің әрбір нұсқаларын оңтайластыру арқылы алынатын максималды пайдалар сомасы есептелінеді және оны нұсқаларды біріктіруші блок дейді. Себебі онда барлық блоктағы айнымалылар бірге қарастырылады және барлық нұсқалар бірге бір есепті шешуге бағытталған. Бірақ оның мәні бойынша ешқандай да шешім қабылдай алмаймыз. Осыдан кейін барлық оңтайластырған, пайдасы максималды мәніне жеткен нұсқалар ішінен пайдасы бәрінен жоғары нұсқа ізделінеді, яғни:
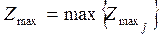 (4.47)
(4.47)
Осы әрекет функционалды, яғни мақсат функцияны анықтау үшін қолданылады.
Сонымен, максималды пайда табу қарастырылған жағдай-дағы есептің математикалық моделі толық құрылды. Келесі кезекте осы құрылған модельді MS Excel-дің жұмыс бетіне кестелік модельге ауыстырамыз.
Кестелік модель тұрғызу туралы арнайы тәсіл жоқ екені белгілі. Дегенмен де, бірінші бөлімде келтірілген ұсыныстарға және 4.9-кестедегі блоктық матрица тұрғызу принципіне сүйеніп, негізгі мақсат талдауға ыңғайлы және MS Excel-дің жұмыс бетіне көрнек-ті сидыру көзделініп, кестелік модель 4.10-суретте көрсетілген қа-лыпқа келтірілді. Осы жерде кестелік модельді MS Excel-дің жұмыс бетіне сидыру үшін, блоктық матрицада қойылған, блоктарды диагональ бойына орналастыру принципі орындалмағанын атап өтейік. Мұндай әрекет есептің нәтижесіне ешқандайда әсер етпейді.
Кестеде жеке әрбір нұсқалар бойынша өзінше бір блок құ-рылған. Онда белгісіздер үшін бөлек ұялар аралығы: 1-нұсқа – $B$4:$D$4; 2-нұсқа – $B$11:$D$11; ...; 6-нұсқа – $B$39:$D$39 қарастырылған.
Бірінші кезекте 1-нұсқада, (4.35) формуламен өрнектелген шектеулер жүйелері, содан кейін (4.34) формула өрнегі: G4:L8 және G9:L9 ұялар аралықтарына орналастырылған. Тура осындай ретпен басқа нұсқалардағы шектеулер жүйелерін: G11:L44ұялар аралықтарына өздерінің тиісті комментарияларымен барлық нұсқаларға сәйкес блоктарды орналастырдық (4.10-сурет).
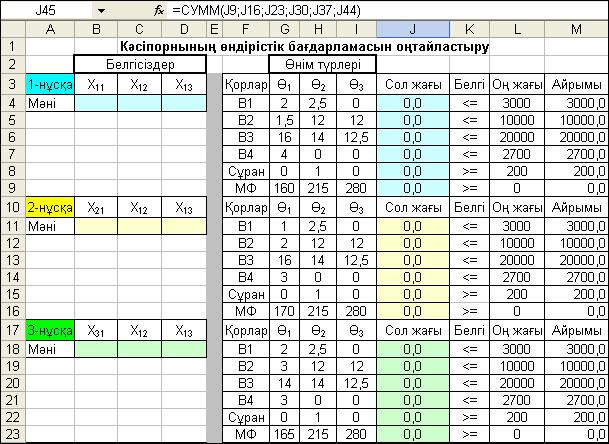

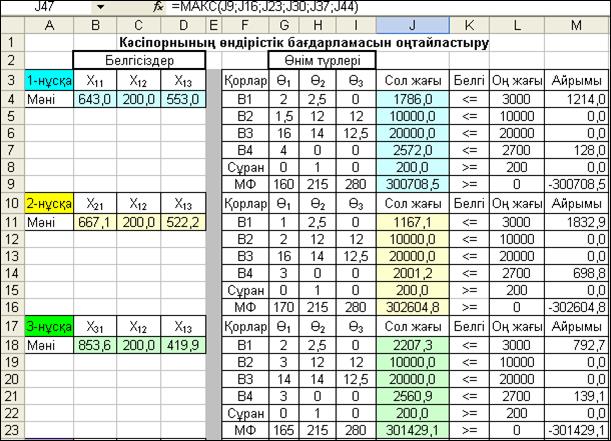
4.10-сурет. Максималды пайда арқылы кәсіпорнының оңтайлы бағдарламасын анықтауға арналған кестелік модель
Сонымен қатар кестелік модельде шектеулердің «оң жағы» және «сол жағы» мәндерінің айрымдары үшін қосымша М4:М44 ұялар аралығын тағайындадық. 4.10-суретте әрбір блоктарда есепті шешу нәтижесінде қызықты көрсеткіштердің мәндері анықталынатын ұялар арнайы түстермен көрсетілген.
4.9-кесте келтірілген блоктарды орналастыру реті бойынша орналасқан кестелік модельдің біріктіруші блогы, яғни 4.46 фор-муладағы көрсетілген технологиялық нұсқалардың мақсат функ-циялар мәндерінің сомасы, J45 ұяда: =СУММ(J9;J16;J23; J30;J37; J44) формуламен есептелінеді. Осы формулада көрсетілген J9, J16, J23, J30, J37 және J44 ұяларда әрбір нұсқалар бойынша мақсат функциялардың максималды мәндері анықталынады. Кестелік модельдің соңғы жолында, әрбір блоктағы мақсат функциялар мо-дельдерінен құралған шектеулердің сол жақтарының: J9, J16, J23, J30, J37 және J44 ұяларда орналасқан мәндері ішінен, J47 ұяда, (4.47) формула негізінде құрылған: =МАКС(J9; J16;J23;J30;J37; J44) формула бойынша пайдасы максималды мәнді нұсқа ізделі-неді.
Кестелік модельді орналастырғаннан кейін Поиск решения құралын іске қосамызда тиісті әрекеттерді орындаймыз. Шектеулер жүйесі әдеттегідей әдістермен енгізіледі. Осы жерде ерекшелік, тек Изменяя ячейки-ге белгісіздер ұялар аралықтарын, мына түрде: $B$4:$D$4; $B$11:$D$11; …; $B$39:$D$39 (4.11-сурет) енгіземіз. Параметры→ Линейная модель, Неотрицательные значения және Автоматическое масштабирование - ғабелгі қойылады.
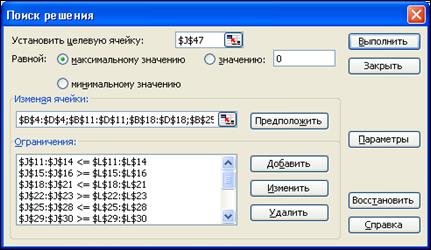
4.11 - сурет. Есепті шешу барысындағы Поиск решения-ның сұхбаттасу терезесі
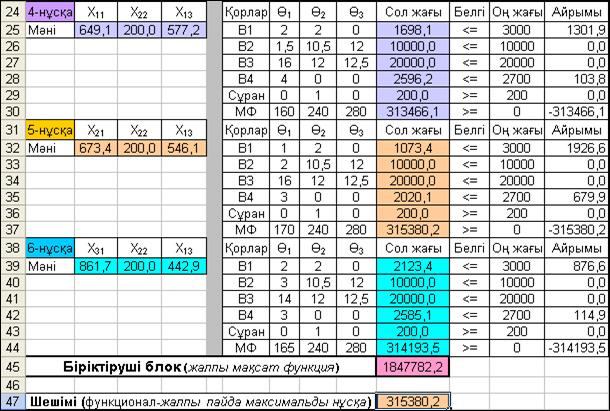
4.12-сурет. Кәсіпорынның оңтайлы бағдарламасы анықталған есептің шешімі
Выполнить батырмасын іске қосқаннан кейін әдеттегідей сұхбаттасу терезесі арқылы Поиск решения есептің шешімі табылғанын хабарлайды.
Есептің шешімі 4.12-сурет көрсетілген. Суретте оңтайлы өндірістік бағдармалар ішіндегі айрықша оңтайлысы 5-нұсқа екені байқалады. Өйткені мақсат функцияның максималды мәні, яғни 315380,2 теңге пайда, тек осы нұсқада алынатыны және өндіріс орны 1-ші өнімді 2-технологиямен: х21= 673.4 ө.б.; 2-ші өнімді де 2-технологиямен: х22 = 200,0 ө.б.(яғни сұраныс көлеміндей) және 3-ші өнімді х13= 546,1 ө.б өндіру керектігі, сонымен қатар өндірістік қорлардың осы нұсқада тиімді қолданылатыны анықталынды. Осы нұсқада қорлар басқаларға қарағанда көп артық қалады. Мысалға, 1-ші қор 1926,6 ө.б., ал 4-ші қор 679,9 ө.б. (2-нұсқа 698,8 ө.б., ескермегенде) артық қалды. Сөзсіз, өндіріс орны қолданылмай қалған қорларды басқа мақсаттар үшін пайдаға асырып, жалпы өндіріс үшін пайда мәнін жоғарлатуы әбден мүмкін.
Қарастырылып отырған есептің екінші критериясы, өнім-дердің өзіндік құнының минималды мәнін іздейтін модель. Енді есепті осы модель бойынша шығарайық. Ол үшін барлық өнім-дердің өзіндік құндарының сомасы, яғни (4.31) формуласының экономикалық-математикалық моделін (біріктіруші блокты) тұрғы-зайық:
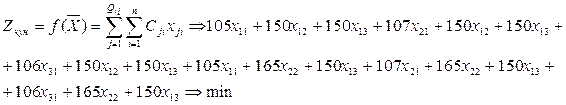
Осы формула мына түрде: =СУММ(E5;E12;E19;E26;E33; E40), кестелік модельде J45 ұяда есептелінеді (4.13-сурет), сөйтіп барлық блоктар бір-бірімен біріктіріледі.
Есептің шарты бойынша берілген, өткен жылғы пайда деңгейін ескерсек, онда (4.33) формула бойынша әрбір блокқа сәйкесінше мындай теңсіздіктер енгізіледі:
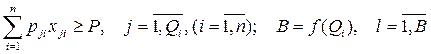 немесе
немесе
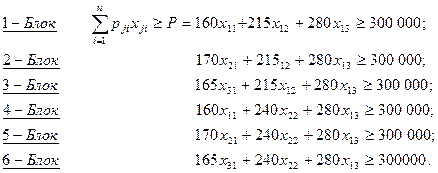
Сонымен, өнімдерді өндіру технологияларының бірлестіріл-ген әрбір нұсқалары бойынша кестеде жеке өзінше бір блок құрылған. Онда белгісіздерді (4.10 және 4.13-суреттер) және өзіндік құндарды есептейтін бөлек ұялар аралығы, сонымен қатар әрбір нұсқалар бойынша олардың нақтылы мәндерін көрсететін (1-Блокта – B5:D5және E5; 2-Блокта– B12:D12 және E12; ...; 6-Блокта – B40:D40 және E40) ұялар қарастырылған (4.11-сурет), яғни:
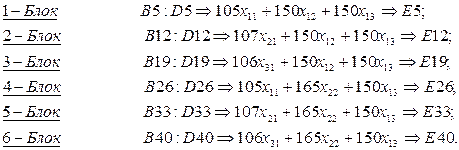
Есептің 1-ші қойлымындағы математикалық модельдің шектеулері толығымен 2-ші қойлымдағы модельге де енгізілетін болғандықтан, алғашқы кестелік модельді осы есепті шешуге де қолданамыз. Өнімдердің өзіндік құндарының минималды мәндерін іздеуге арналған және осындай мақсатта түзетілген кестелік модельдің алғашқы қалпы 4.13-суретте көрсетілген.
Кестелік модельдің соңғы жолында, әрбір блоктағы мақсат функциялар мәндері ішінен, J47 ұяда, (4.47) формулаға керісінше құрылған: =МИН(E5;E12;E19;E26;E33;E40) формула бойынша өзіндік құны минималды мәнді нұсқа ізделінеді.
Выполнить батырмасын іске қосқаннан кейін есептің шешімі алынғаны туралы әдеттегідей сұхбаттасу терезесі арылы хабар-ланады да, есептің шешімі 4.14-суретте көрсетілген кейіпте экран-да көрінеді.
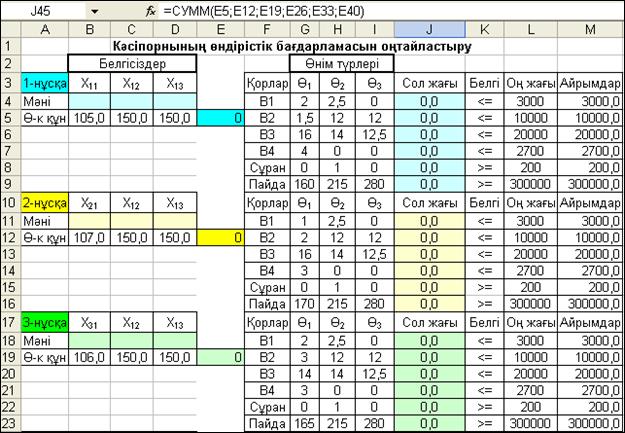
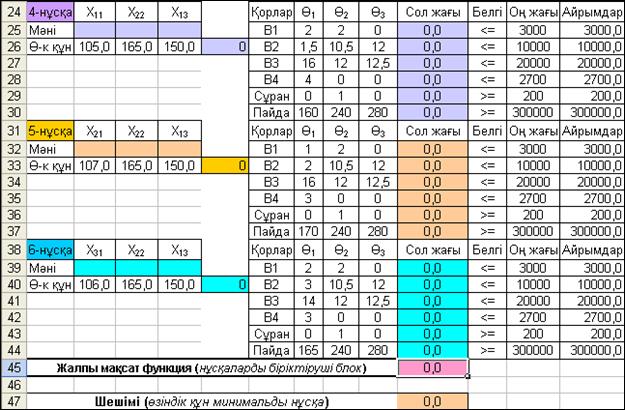
4.13-сурет. Минималды өзіндік құн арқылы кәсіпорынның оңтайлы бағдарламасын анықтауға арналған кестелік модель
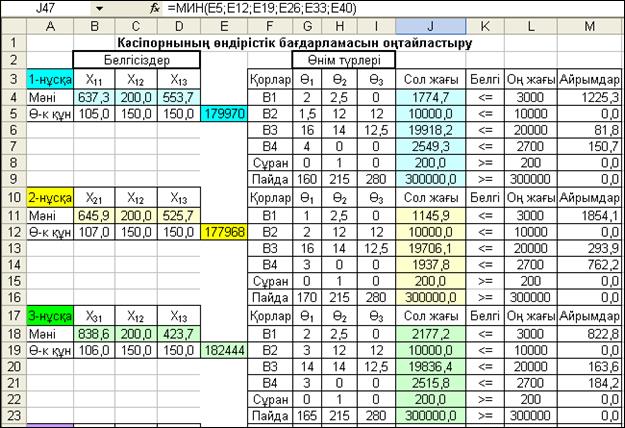
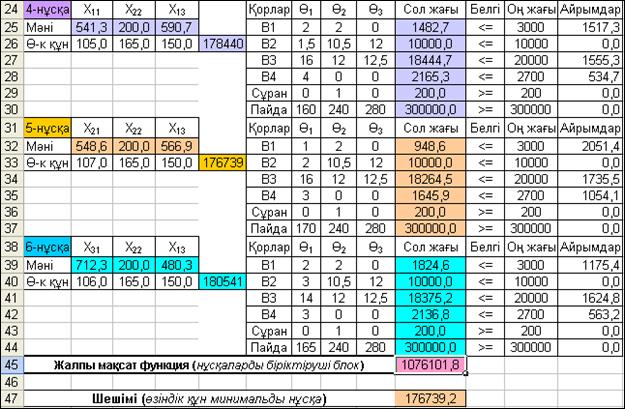
4.14-сурет. Кәсіпорынның оңтайлы бағдарламасы анықталған есептің шешімі
Сонымен, екінші критериямен есепті шешу нәтижесінде тағы да оңтайлы өндірістік бағдарламалар ішіндегі айрықша оңтайлысы 5-нұсқа екенін 4.14-суреттен көріп отырмыз. Суретте мақсат функцияның (өнімнің өзіндік құндар сомасының) минималды мәні 176739,2 теңгеге тең. Өндіріс орнына тек 5-нұсқамен, яғни 1-ші өнімді 2-технологиямен: х21= 548,6 ө.б.; 2-ші өнімді де 2-техноло-гиямен: х22 = 200,0 ө.б., яғни сұраныс көлеміндей және 3-ші өнімді х13= 566,9 ө.б өндіру тиімді екені анықталынды. Алдыңғы шешім-дегідей өндірістік қорлардың осы нұсқада тиімді қолданылатыны, яғни басқа нұсқаларға қарағанда 5-нұсқада қолданылмай қалған қорлар мөлшері анағұрлым көп екені анықталды. Мысалға, 1-ші қор 2051,4 ө.б., 3-ші қор 1735,5 ө.б. және 4-ші қор 1054,1 ө.б. артық қалды. Сөйтіп, 5-блокта модельденген, өндіріс орнының өнімдерді өндіру технологияларының бірлестігі ең оңтайлы екені дәлелденді.
Қарастырылып отырған есеп сызықтық модельдеу есептері-не жатады. Поиск решениясызықтық модель есебін шешу нәти-жесінде үш қортынды есептерін берілетіні белгілі. Оның ішінде нәтиже бойынша есебінде әдеттегі нәтижелерден (белгісіздердің мәндері, шектеулердің оң және сол жақтарының айрымдары, сонымен қатар қор толық қолданылса шектеу байланысты, ал керісінше жағдайда байланыссыз делінетін жағдай) басқа ерекше атап өтетіндей қызықты ештеңеде байқалмады.
Қортынды есептердің ішінде орнықтылық есебі бір шама қызықты. Осы есепте екі кесте алынады. Қарастырылып отырған негізгі есепті екі критериямен шешу барысында алынған орнық-тылық есебінің 1-ші кестесінің нәтижесі, біздің біраз түзетулерден кейінгі кейпі, 4.15-суретте көрсетілген.
Орнықтылық есебінде (4.15-сурет) қосымша қосалқы айны-малы (vі)барлық жағдайда нөлге тең. Себебі қарастырылып отырған нұсқаларда жоспарланған өнімдердің барлығында өндіру тиімді болып отыр.
Дегенмен де, өндіріс орнының экономикалық потенциалдық мүмкіншілігіне толық жетуге 2-ші өнімге қойылған қатаң сұраныс мөлшері (200 ө.б. кем емес) кедергі жасауда. Ондай жағдай айнымалылардың табылған мәндері өзгеріссіз қалған жағдайда, мақсат фукция коэффициенттері қандай аралықтарға дейін өзгеретінін көрсететін, Допустимое увеличение және Допустимое уменьшение бағаналарындағы мәндерден де байқалады. Мысалға, 2-ші өнімнің бір бірлігінің бағасы мақсат функция максимумге ізделгенде ең үлкен санға кемісе, ал керісінше жағдайда ең үлкен санға өседі. Өндіріс орнының табылған оңтайлы бағдарламасының орнықты болуы 3-ші өнімнің бір бірлігінің бағасына да байланысты (4.15-сурет).
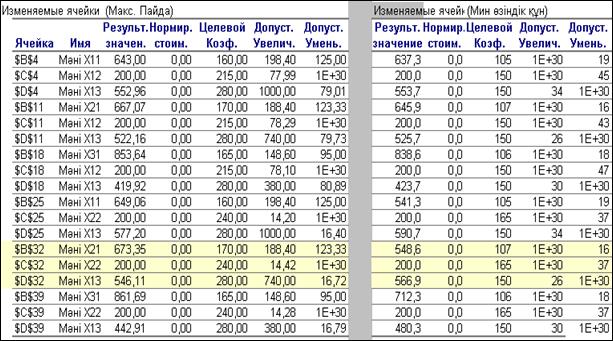
4.15-сурет. Орнықтылық есебінің 1-ші кестесі
Орнықтылық есебінің 2-кестесінде де шектеулер үшін 1-кестедегі сияқты көрсеткіштер беріледі (қорлардың қолданылған шамасы; көлеңкелік құн немесе шектеулердің қосалқы бағалары–уі). Есепті максималды пайдаға және минималды өзіндік құнға шешкендегі, сәйкесінше 4.16 және 4.17-суреттерде орнықтылық есебі бойынша 2-ші кестелердің нәтижелерінің фрагменттері көрсетілген. Кесте де қызықты көрсеткіш, ол көлеңкелік құн. Қор толық қолданбаса көлеңкелік құн нөлге (уі = 0) тең болатыны белгілі. Біздің мысалда, (4.16-сурет) 5-ші оңтайлы нұсқада 1-ші жә-не 4-ші қорлар толығымен қолданылмады, қосалқы бағалар: у1= 0 және у4 = 0. Өндіріс орнында 2-ші және 3-ші қорлар тапшы, қосалқы бағалары, сәйкесінше: у2=14,1 және у3 = 8,9. Егер 2-ші қор шамасы бір бірлікке өсетін болса, онда мақсат функция мәні 14,1 шамаға көбейеді, керісінше жағдайда сонша мәнге азаяды. Осындай пікірді 3-ші қор бойынша да, яғни осы қордың бір бірлікке өзгеруіне байланысты мақсат функция мәні 8,9 шамаға өзгеретінін айтуға болады.
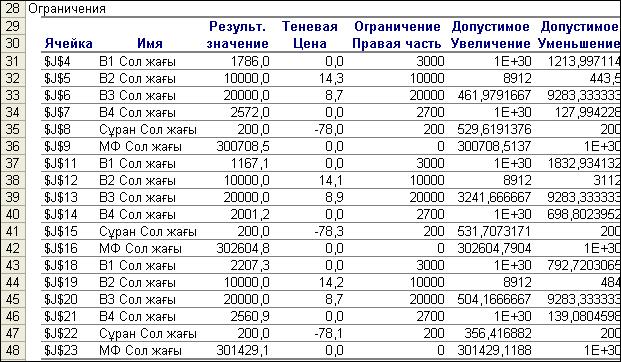
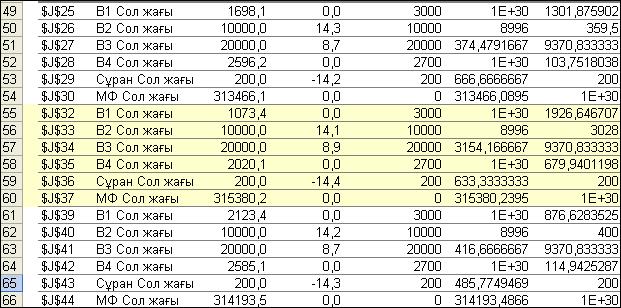
4.16-сурет.Есепті максималды пайдаға шешудегі орнықтылық есебінің 2-кестесі
4.16-суреттен көріп отырмыз, өндіріс орнына 2- өнімді өндіру тиімді емес. Сұраныс талабы бойынша қойылған, 2-ші өнімді 200 ө.б. кем емес өндіру шектеуінің қосалқы бағасы (у5 = -14,4), яғни өнімге сұраныс бір бірлікке көбейсе: Z=315380,2 –1·14,4 =315365,8 немесе бір бірлікке азайса: Z=315380,2 + 1·14,4 = 315394,6. Келтірілген есептеулер тек 5-ші оңтайлы нұсқа бойынша қарасты-рылып отыр. Бірақ, 1-ші, 2-ші және 3-ші нұсқалардың оңтайлы шешімдерінде 2-ші өнімге сұраныс шектеулерінің қосалқы бағалар (у5) мәні кемінде 5 есеге дейін өскен (-78,3). Сонымен осы көрсет-кіш бойынша басқа нұсқаларға қарағанда тағы да 5-ші нұсқаның ұтымды екені дәлелденді.
Есепті минималды өзіндік құнға шешкенде (4.17-сурет) тағы да жоғарғыдай нәтижелерді алдық. Шешімде 5-ші оңтайлы нұс-қада 1-ші, 3-ші және 4-ші қорлар толығымен қолданылмады, қосалқы бағалар: у1=0, у2=0 және у4=0. Өндіріс орнында 2-қордың тапшы екені тағы да дәлелденді, оның қосалқы бағасы (у2= -3,0) теріс мәнді, яғни оның бір бірлікке өсуі мақсат функция мәнін кішірейтеді. Демек, өзіндік құнның шамасы 3 ақша бірлігіне кемиді.
Өндіріс орнына 2-ші өнімді өндіру тағы да тиімді болмай шықты. 2-ші өнімді 200 ө.б. кем емес өндіру шектеуінің қосалқы бағасы (у5 = 37,1), яғни өнімге сұраныс бір бірлікке көбейсе: Z =
= 176739,2 + 1·37,1 = 176770,3 немесе бір бірлікке азайса: Z=176739,2 – 1·37,1 =176702,1.
Шекаралық есеп бойынша шешім құрамын сақтай отырып, оңтайлы шешімге енген өнім мөлшерін қанша аралыққа дейін өзгертуге болады деген сұраққа жауап алынатыны белгілі. Біздің жағдайда оңтайлы шешімде алынған көрсеткіштердің шамалары шеткі ең жоғарғы мәндеріне сәйкес, ал олардың төменгі мәндерін нөлге дейін өзгертсек те оңтайлы шешімде алынған өнім құрамы өзгермейді.
Сонымен, қарастырылып отырған мысал бойынша тәжіри-белік есептердің шешу тәсілін оқып, зерделеу біздің негізгі мақсат болатын, біз оған жеттік деп ойлаймыз. Ал оқу үшін қарастырыл-ған мысалда кездескен қызықты мәліметтерді талдауды аяқтадық. Дегенімен де, әлі де болса шешімді талдау толық бітпейтінін тағыда ескертеміз. Тәжірибелік есептерді шешкенде толық талдау жасау барысында, бірнеше өндірістік қызықты сұрақтарға жауаптар алынатыны даусыз.
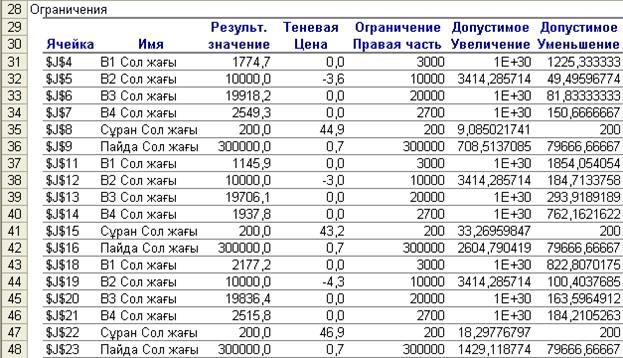
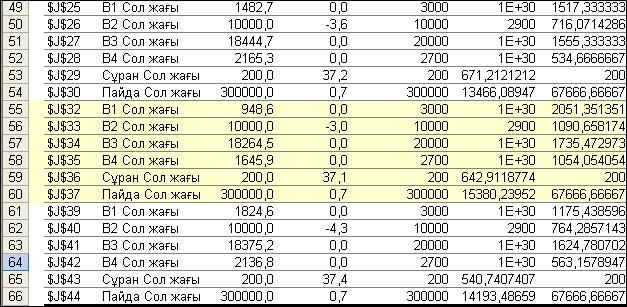
4.17-сурет. Есепті минималды өзіндік құнға шешудегі орнықтылық есебінің 2-кестесі
4.4 «Қоспа» есебінің моделі
Тәжірибеде «Қоспа» есебі ең маңызды есептердің қатарына жатады. Оның терең мәнді, өзекті есептердің бірі болуын, даму тарихынан да байқауға болады. Осы есептің авторы Джон Стиглер оның алғашқы математикалық моделін 1945 жылы жанұясының тіршілігіне байланысты құрастырғанына қарамастан, ол адамзат өміріндегі барлық салаларда қолдану тапты. Ал Дж. Стиглер Нобель лауазымының иегері аталды. Ол бүгінгі таңда кез келген қоғамда халық шаруашылығының біраз салаларында көп қол-данылатын есептердің бірі. Мысалға, агроөнеркәсіп салаларында «Мал шаруашылығында рацион құру», «Тыңайтқыштардың оңтай-лы құрамын анықтау», «Жемшөп қоспасының оңтайлы құрамын анықтау» және т.б. Бастапқы кезде әдебиеттерде осы типтес есеп-терді «Диета туралы» есептер деп атады. Осы атауға байланысты саудасаттық салаларда «Тиімді тамақтану азықтарын жоспарлау» есебі қазіргі экологиялық жағдайларға байланысты адамзат өмірін-дегі өте маңызды есептерге айналды.