Главная | Обратная связь

Тапшысымен тасымалдау есебі 9 страница

Кестеден көріп отырмыз, әрбір тоқсаның басында әрбір жоба инвестицияланылады, яғни ақша іске салынады. Бірінші жобаға 4 тоқсан бойы ақша салынса, екіншіге 5 тоқсан, ал қалған жобаларға 6 тоқсан бойы ақша салынады. Сонымен қатар есепте басқада талаптар болуы мүмкін. Мысалға, бірінші және екінші жобалардан түсетін пайдалар арқылы қалған жобаларды 5-ші және 6-шы тоқсандарында инвестициялау жағдайды қарастыруға болады. Әзірше мұндай талапта, есептің қойылуын қарастырмаймыз.

Шешуі. Қойылған есепті шығаруды ең қарапайым нұсқадан бастайық. Компанияның П1, П2, П3, П4 және П5 жобаларға қатысу дәрежелерін сәйкесінше х₁, х₂, х₃, х₄ және х₅ деп белгілейік. Қабылданған белгісіздер 0 - ден (жобаға қатыспайды) 1-ге дейін (жобаға қатысады) өзгеретін болсын. Сонымен, біз әзірше айны-малыларды 1-ші типегілер және 2-ші типтегілер деп бөлмейміз. Мұндай бөлуді кестелік модельдер құрған кезде жүргіземіз.

Айнымалыларды 1-ші және 2-ші типтерге бөлу жоғарыда осы бөлімде баяндалды. Мысалға, айнымалылар типтері мынадай шарт-тарға байланысты анықталынады. Бірінші шарт, егер i-инвестр жобаны таңдап алса, онда ол жобаның сұранысын толық қанағат-тандырады (х_i=1), жобаны таңдамаса (х_i=0), мұндай жағдайда 1-ші типтегі бульдік айнымалылар қабылданылады. Екінші шарт, егер i-инвестр жобаны толық қанағаттандырмай, тек оған өз үлесімен ақша салатын болса, онда х_i – 0-ден 1-ге дейін үздіксіз өзгеретін шамаға айналады да, оны 2-ші типтегі айнымалы деп атайды. Ескерту: Екінші шарт жағдайында инвестрге түсетін пайда, оның жобаға үлестік қатынасына байланысты есептелінеді.

Жалпы табыс сомасы барлық жобаларды іске қосқаннан кейін есептелінеді деп есептеп, максимальды мәні ізделінетін мақ-сат функцияны былай өрнектейміз:

Z= 1170 x₁ + 2035x ₂ + 2375x₃ + 1280x₄ + 2890x₅

Келесі кезекте инвестрдің тоқсан сайын инвестициялауға арналған бос қаржыларының шектеулерін жазамыз:

4495 x₁ + 2050x₂ + 930x₃ + 2610x₄ + 1000x₅ ≤ 10000,

1100 x₁ + 1495x₂ + 3865x₃ + 1020x₄ + 2230x₅ ≤ 10000,

1985 x₁ + 635x₂ + 965x₃ + 1550x₄ + 2795x₅ ≤ 7500,

2025 x₁ + 3850x₂ + 875x₃ + 4730x₄ + 2570x₅ ≤ 12500,

0 x₁ + 2440x₂ + 1550x₃ + 4015x₄ + 2565x₅ ≤ 10000,

0 x₁ + 0x₂ + 2615x₃ + 4990x₄ + 3005x₅ ≤ 10000.

Бұл шектеулерден басқа, бірінші типтегі айнымалылар үшін екілік болу шарты, айнымалылардың теріс болмау шарты және екінші типтердегі айнымалылар үшін мынадай: x₁ ≤1, x₂ ≤ 1, x₃ ≤ 1, x₄ ≤ 1 және x₅ ≤ 1 шектеулер жазылады.

Осы құрылған математикалық модельдер негізінде белгілі тәсілмен MS Excel-дің жұмыс бетіне кестелік модель құрамыз. Құрылған кестелік модель 5.5-суретте келтірілген және осы суретте инвестр барлық жобаларды таңдағандағы жағдай қарастырылған, яғни мәндері ізделініп отырған айнымалылар бірінші типтік деп қабылданған. Ол үшін олардың барлығы да бірге теңестірілген (5.6-ші суретті қараңыз).

 

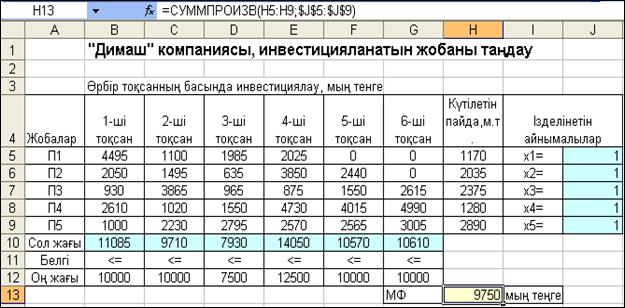
5.5-сурет. Инвестр барлық жобаларды таңдағандағы есептің нәтижесі

 

 

5.6-сурет. Инвестр барлық жобаларды таңдағандағы шарттың жазылуы

Есептің 1-нұсқада шығару нәтижесінен, егер инвестр барлық жобаны таңдаса, 2-ші тоқсанан басқа тоқсандарда жобаларды ақ-шамен толық қанағаттандыра алмайтынын байқаймыз. Демек, мақсат функцияның есептелген мәніне, инвестр толығымен инвес-тициялау талабын орындағанда жетуге болады. Инвестрдің қаржы-сы шектеулі болғандықтан бұл нұсқа тәжірибеде орындалмайды.

Енді есепті 2-нұсқада, яғни инвестр өзінің қаржысының жеткенінше, пайдалы жобаларды таңдау жағдайларын қарасты-райық. Есептің шарты бойынша инвестр бірінші кезекте, таңдалған пайдалы жобаны ақшамен тоқсан сайын толық қамтамасыздан-дырады немесе оны қабылдамайды. Мұндай жағдайда мәндері ізде-лінетін айнымалылар екілік болып есептелінеді, яғни олар, тек екі мән (0 немесе 1) қабылдайды. Жоба қабылданса х_і =1 немесе қабылданбаса х_і =0.

Есепті енді екілік айнымалылармен шешеміз. Ол үшін Поиск решения құралын іске қосып, J5:J9 аралықтағы ұяларға екілік шартты жазамыз (5.7-суретті қараңыз). Осы жағдайда айнымалы-лардың теріс болмау шартын жазудың немесе параметр-де белгі-леудің қажеті жоқ.

5.7-сурет. Екілік айнымалы есеп үшін Поиск решения–ның сұхбаттасу терезесі

 

Екілік айнымалылармен шешілген есептің нәтижесі 5.8-сурет-те берілген. Көріп отырсыз, бұл шешімде алынған табыс айтарлық-тай көп емес және инвестрге 4-ші жобаға ақша салу тиімсіз (х₄ нөлге тең). Сонымен қатар, инвестициялауға бөлінген ақша толық қолданылған жоқ. Сөзсіз, бұл ойланатын жағдай. Сондықтан бұдан да ұтымды инвестициялау нұсқасын қарастырған жөн.

 

5.8-сурет. Екілік айнымалылармен жобаларды таңдау есебінің нәтижесі

5.9-сурет. Үздіксіз айнымалы есеп үшін Поиск решения–ның сұхбаттасу терезесі

Енді есепті екілік шартсыз, яғни инвестрге кейбір жобаларды оған керекті мөлшерде ақшамен толық қамтамасыздандырмай, өз мүмкіндігінше үлеспен инвестициялауға қатысатын жағдайды қа-растырайық. Есеп екінші типті үздіксіз мәнді айнымалыларға ауы-сады. Демек, J5:J9 аралықтағы ұяларға х_і ≤ 1 шартын жазамыз (5.9-суретті қараңыз) және Параметр-дегі белгісіздердің теріс болмау шартын белгілі тәсілмен белгілеуді ұмытпаңыз.

 

 

 

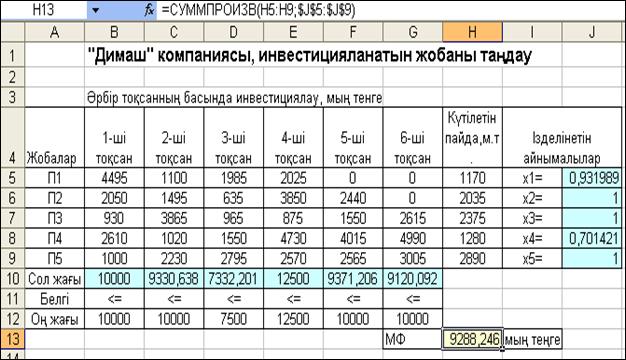
5.10-сурет. Үздіксіз айнымалылармен жобаларды таңдау есебінің нәтижесі

 

Есепті MS Excel-де шығару нәтижесі 5.10-суретте көрсетіл-ген. Сөйтіп, инвестрдің екінші, үшінші және бесінші жобаларға толық, ал бірінші жобаға 93% деңгейінде және төртінші жобаға 70% деңгейінде қатыса алатынын суреттен байқадық. Осы жағ-дайда инвестрдің табысы ең жоғары (9288,246 мың теңге) деңгейге жететініне көз жеткіздік. Осы нұсқада алынған табыс алдыңғы нұсқадағы нәтижеден 9288,246 – 8470 = 818,246 мың теңге артық. Инвестрдің инвестициялауға жұмсауға жоспарланған бос қаражаты толық дерліктей қолданылды.

Сонымен ақырғы нұсқада шығарылған есептің нәтижесін оңтайлы шешім деп қабылдау толығымен дәйекті.

5.2.2 Тапқан пайда арқылы инвестициялау

Жоғарғы бөлімде талқыланған есептің алғашқы шартын өзгертпей, бірінші және екінші жобалардан түсетін пайда арқылы 5-ші және 6-шы тоқсандарда инвестициалау жұмысын жүргізу үрдісін қарастырайық.

0х₁ + 2440х₂ + 1550х₃ + 4015х₄ +2565х₅ ≤ 10000 + 1170х₁у₁

немесе

–1170х₁у₁ + 2440х₂ + 1550х₃ + 4015х₄ +2565х₅ ≤ 10000.

Сөйтіп, алтыншы тоқсанда да осы әрекеттерге сәйкес мүмкін бола алатын инвестициялардың сомасы, мына: 1170 х₁ (1-у₁) + +2035х₂у₂ мәнге өседі. Сондықтан, осы тоқсанға сәйкес мынадай шектеу құрамыз:

0х₁+ 0х₂ + 2615х₃ + 4990х₄+3005х₅ ≤ 10000 + 1170 х₁ (1-у₁) + 2035х₂у₂

немесе

–1170 х₁ (1-у₁) – 2035х₂у₂ + 2615х₃ + 4990х₄ +3005х₅ ≤ 10000.

 

5.11-сурет. Жаңа есеп үшін кестелік модель

Математикалық модельдің шектеулер жүйесіндегі соңғы екі шектеуді, алынған шектеулермен ауыстырамыз. Шектеулерде ай-нымалылардың көбейтіндісі х₁у₁ және х₂у₂ пайда болуына бай-ланысты, алғашқы математикалық моделіміз сызықтықтан сызық-ты емес модельге ауысқанына көңіл аударыңыз.

Жаңа есеп үшін кестелік модель 5.11-суретте бейнеленген. Мұнда L5 және L6 ұяларда жаңа айнымалылардың мәндері орна-лысады. Бесінші тоқсан үшін қойылған теңсіздіктің сол жағын есептеуге мынадай формула:

=СУММПРОИЗВ(F5:F9; $J$5:$J$9) – H5*J5*L5,

ал алтыншы тоқсан үшін теңсіздіктің сол жағын есептеуге мынадай формула жазылады:

=СУММПРОИЗВ(G5:G9;$J$5:$J$9) – H5*J5*(1–L5) – H6*J6*L6.

.

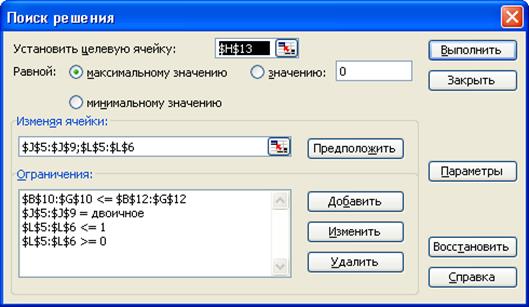
5.12-сурет. Екілік айнымалы жаңа есеп үшін Поиск решения-ның

сұхбаттасу терезесі

Жаңа есепті айнымалылардың х₁, х₂, х₃ , х₄ және х₅ екілік болу шарты бойынша шығарамыз. Осы жағдайдағы Поиск реше-ния-ның сұхбаттасу терезесі 5.12-суретте көрсетілген. Көріп отыр-сыз, ұяшықтар полясына L5:L6 ұялары қосылған, шектеулер тізіміне қосымша L5:L6 <=1 және L5:L6 >= 0 шектеулері енген. Поиск решения-ның Параметры –дағы Линейная модель-ден флажокты алып тастаймыз да, Поиск решенияқұралын іске қосамыз.

Жаңа есептің шешімі 5.11-суретте көрсетілген. Жаңа есепті шығарғанда алынған нәтижелер толығымен жоғарғы бөлімде есепті екілік айнымалылармен шығарған нәтижені қайталады. Сонымен, жалпы пайданың сомасы өспеуіне байланысты бірінші және екінші жобаларға түскен пайдамен инвестициялау жұмысын жүргізу тиімді емес. Дегенмен де, теріс нәтиже – ол да нәтиже. Бірақ, әліде тексерілмеген басқа да нұсқалар бар. Сондықтан жоғарыдағы кел-тірген тұжырым ертерек емес пе?

Осы жерде, қабылданған жаңа айнымалылар у₁ және у₂ бойынша көптеген есептің шешімдерін алуға болатынын, атап өтейік. Бірақ ізделініп отырған басты айнымалы х_і өзінің мәнін өз-гертпеуіне байланысты олардың нәтижелері қызықты емес.

 

5.13-сурет. Айнымалылары үздіксіз жаңа есеп үшін Поиск решения-ның сұхбаттасу терезесі

 

Енді пайда есебі арқылы толық емес, үлес түрінде жүргізетін инвестициялау нұсқасын қарастырайық. Егер 5.10-суретте келтіріл-ген есептің шешіміне ой салып талдасаңыз инвестициялық қорлар бесінші және алтыншы тоқсандарда 5-ші және 6-шы шектеулер үшін тапшы емес. Сондықтан осы қорлардың қосымша өскені есептің шешіміне ешқандай да әсер етпейді. Бірақ бұл тұжырымды дәлелдеу керек. Осы нұсқада есепті шешу үшін 5.11-суретте келті-рілген кестелік модельді пайдаланамыз. Есепті шығару барысында Поиск решения-ның сұхбаттасу терезесі 5.13-суреттегідей болып көрінуге тиіс. L5:L6 ұялар аралығы айнымалылар полясына және шектеулер тізіміне L5:L6<=1 – шектеуі қосылады. L5:L6>=0 – шек-теуі берілмейді. Себебі барлық айнымалылардың теріс болмау шар-тты міндетті түрде белгіленуге тиіс. Линейная модель-ден фла-жокты алып тастаймыз.

 

5.14-сурет. Айнымалылары үздіксіз жаңа есептің шешімі

 

Есептің шешімі 5.14-суретте көрсетілген. Көріп отырмыз, шешім нәтижесі толығымен 5.10-суреттегі көрсетілген нәтижені қайталады. Оны дәлелдеу керек болатын. Олай болса, біз оны дәлелдедік (5.10 және 5.14 суреттердегі нәтижелерді салысты-рыңыз, көзіңіз жетеді).

Сонымен, жалпы пайданың сомасы өспеуіне байланысты бірінші және екінші жобаларға түскен пайдамен инвестициялау жұмысын жүргізу «Димаш» компаниясы үшін тиімді емес деген шешім қабылдаймыз.

 

 

5.3 Мақсаттық қаржылық қорды құру есебі

Ақшаны өсім пайызына салудың әртүрлі тәсілдері және әдістері болатыны бүгінгі кезде әркімге белгілі. Сөзсіз, кім де болса өсім пайызына ақшаны минимальды мөлшерде салып, максималь-ды табыс немесе пайда табуға тырысады. Сондықтан, салымнан максимальды табыс алу үшін, оны іске қандай тәсіл және әдіспен салған тиімді деген еріксіз сұрақ туады.

Тәжірибеде мұндай есептерді қаржыларды жоспарлау есебі деп атайды. Есепте өте маңызды және күрделі мәселелердің бірі тәуекелділік (риск) көрсеткішінің мәнін дәйектеу және анықтау. Сонымен қатар басқа да факторлардың өсімге салған қаражатқа әсерін нақтылы дұрыс анықтаған маңызды.

Қарастырылып отырған есепті ретке келтіру мақсатында (формализация) мынадай сөздіктерді енгізейік:

– салым – іске салған ақша;

– алдын-ала жиналған ақша – мақсаттық қаржылық қор;

– салым бойынша тәуекелділік (риск) индексі.

Тәжірибеде қаржыларды жоспарлау есебінің бірнеше нұсқа-лары кездеседі. Біз мақсаттық қаржылық қорды минимальды мөлшерде іздеу деп аталатын қаржыларды жоспарлау есебінің А–нұсқасын қарастырамыз.

Айталық, бір мезгілде салымға салған немесе несиеге беруші қарызға берген қаражатты қайтару керек, яғни қарызгер немесе банк нақтылы бір соманы төлеуге тиіс. Осы соманы төлеу үшін қарызгер немесе банк алдын-ала бір қаражатты жинақтайды. Осындай мақсатта жинақталған қаражатты мақсаттық қор деп атаймыз.

Салым қысқа мерзімге салынсын. Бұл жерде қысқа мерзімдік деп салымның салған уақытымен оны қайтарған уақыт аралығы айтылады және осы мерзімде салымнан түскен табыс та анықталуға тиіс.

Сонымен, есептің мақсаты мақсаттық қордың минимальды мөлшерін анықтайтын және қарызды өтеуге жұмсалатын салым түрлерін таңдау.

Оқылып, зерделенетін көрсеткіштерді мынадай символдармен белгілейік:

Y – бір мақсат үшін алғашқы салынған салым мөлшері (қаржыландыру әрекетінің басында уақыт мезгілі нөлге тең деп есептелінеді, t = 0);

t – ағымдағы уақыт белгісі (t = 0, 1, …, T);

C_t – t - уақытта (t = 1, 2, …, T) төленген ақша мөлшері;

j – тез мерзімді салым индексі, j=1, 2, …, n;

v_j – тез мерзімді j - салымның салынған уақыты;

w_j – тез мерзімді j - салым бойынша қаражатты қайтару

мерзімі;

r_j – тез мерзімді j - салымнан алынатын табыс;

x_j – тез мерзімді j - салымның алғашқы мөлшері.

T– займды (салымды қанша жылға, уақытқа) берген мерзімнің мөлшері;

n – салымдар саны.

Кез келген тез мерзімді j салым v_j уақытта салынған мөлше-рі белгілі және ол есепке алынған деп санайық.

Егер тез мерзімде j салымның алғашқы мөлшері x_j болса, онда w_j – қаражатты қайтару мерзімінде банк немесе несиеге алушы (қарызгер) мына мөлшерде (1+r_j)x_j ақшаны клиентке қайтаруға міндетті. Қоғамда болып жатқан әртүрлі шектеулер ескерілмей, кез келген уақыт мезгілінде төлей алатындай салым салынған деп есептейік. Кез келген уақыт мезгілінде төлей алатын салымдардың табысы нөлге тең болуы мүмкін. Нөлдік табысты салымды қолдану ақша активтенбегендігін көрсетеді, яғни мағынасы ақша иесінің қолында қалғанмен бірдей.

Осындай талдау жүргізе отырып, әрі қарай есепті қалыптас-тыра беру үшін, тағы да мынадай символдарды енгізейік.

Айталық,

немесе j = 1, 2, …, G_t,

мұндағы G_t – t – уақыт мезгіліндегі салымшыларсаны,олай болса бұл көптік тек уақыт t= v_j, яғни j – ші салымға t уақыт мезгілінде ақша салынған.

Демек, ақшаны қайтару әрекетін де осындай символдармен белгілеп, аламыз:

немесе j = 1, 2, …, Q_t,

мұндағы Q_t – t - уақыт мезгіліндегі төленген салымдар саны, яғни мына уақыт t = v_j+w_jмерзімінде j - ші салым өтелген.

Сөйтіп, кез келген t-уақыт мезгілінде G_t және Q_t белгілі болатынын байқаймыз.

Жоғарыдағы қабылданған символдарды қолданып, есептің математикалық моделін жазайық:

(5.8)

Мына жағдайда:

(5.9)

(5.10)

(5.11)

(5.12)

Математикалық модельдегі (5.8) формула мақсаттық қаржы-лық қордың минимальды мәнін іздейтін мақсат функциясы. Атал-ған функцияның минимальды мәні қаржы әрекеттерінің барлық талабының орындалуын қамтамасыз етуге тиіс, яғни мынадай жағ-дайларда:

– қаржы әрекеттері әлі басталған жоқ, яғни уақыт мезгілі нөлге тең, ал мақсаттық қор салымдарға бөлінген және барлық салымдардағы сомамен мақсаттық қордың айрымы нөлге тең (5.9–ші шектеу);

– төленген сомалармен салымдар сомаларының баланыстық қатынасын көрсететін шектеу (5.10–ші шектеу). Формуладағы B_t – – t - уақыт мезгіліндегі пайыздық ақша мөлшері немесе табыс мөлшері;

– пайыздық ақшаларымен қоса салымшыларға төленген қаржы мөлшері немесе займға алынған қаражатты қойылған мерзі-мінде өтеуді қамтамасыздандыру шарты (5.11–ші шектеу);

– мақсаттық қорды құру және салымға ақшаны салу тиімді немесе тиімсіз, яғни математикалық тілде айнымалылардың теріс болмау шарты (5.12–ші шектеу).

Табыстың максимльды мәнін іздейтін қаржыны жоспарлау есебінің тағы бір нұсқасын (В нұсқасы) қарастырайық. Айталық, са-лымшы бір уақыт аралықтарында максимальды пайда табу үшін, қаражатын салымға салсын. Есеп мақсаттық қордың бекітілген бел-гілі бір мөлшерінде, барлық тез мерзімдік салымдар ішінен макси-мальды табысты қамтамасыз ететіндерін таңдап алу керек.

Жоғарыдағы келтірілген символдарменқатар тағы да мына-дай белгілерді қабылдайық:

B_t – салымшылардың T-уақыт мезгілінде алған табысы;

A_t – t - уақыт мезгілдерінде салынған салым мөлшерлері (t = 1, 2, …, T).

Келесі кезекте есептің математикалық моделін тұрғызайық.

Табыс максимальды болуын көрсететін мақсат функция:

(5.13)

Мына жағдайда:

– бастапқы уақыт мезгілінде мақсаттық қордың салымдар бойынша бөлінуін сипаттайтын шарт:

(5.14)

– төленген сомалармен салымдар сомаларының баланыс-тық қатынасын көрсететін шарт:

(5.15)

– табыс шамасын анықтайтын шарт:

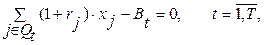(5.16)

– ешқандай табыс ала алмаймыз немесе аламыз және са-лымға ақшаны салу тиімді немесе тиімсіз, яғни математикалық тілде айнымалылардың теріс болмау шарты:

(5.17)

1. Ақшаны пайыздық үстемеге салу. Фермер көксөкті сақтауға арналған құралды сатып алу үшін, осы құралды шыға-ратын кәсіпорынмен келісім-шартқа отырды.

Құралды өндіріске қоятын кәсіпорынға келісім-шарт бойын-ша фермер 750 млн. теңге төлеуге тиіс. Келісім шартта бірінші екі ай өткеннен кейін 150 млн. теңге, ал қалған 600 млн. теңгені алты айдан соң, құралды өндіріске енгізгізіп, сынақтан өткізгеннен кейін төлеу керектігі көрсетілген.

5.4–кесте. Салым салу тәсілдерінің алғашқы мәліметтері

Салым салу нұсқалары	Салым ұзақтығы, ай	Салым салу уақыты мезгілдері (ай басы)	Пайыздық үстемесі, %
А		1,2,3,4,5,6	1,5
В		1,3,5	3,5
С		1,4	6,0
D			11,0

 

Фермер келісім-шарт жасалған күннен бастап мақсат қорын жинақтауға кірісті. Мақсат қор жинақталғаннан кейін қаражатты белсендіру үшін (активтендіру), ол депозитке қойылмақшы. Сөзсіз, мұндай іс–әрекет фермердің қаражатын өсірудің бір тәсілі. Мақ-саттық қор фермер сатып алатын құралдың құнынан (750 млн. теңгеден) айтарлықтай аз болуы керектігін жақсы түсінеді. Деген-мен, құралдың құнын толық төлеген кездің өзінде, өсім салымына қойған қаражат, оған бір шама көп те болуы мүмкін. Бірақ фермердің инвестрлік мүмкіншілігі келісім-шартта көрсетілген әрекеттердің уақытында орындалуын қамтамасыздандыра ала ма? Мүмкін мақсаттық қор көпте болар, онда фермерге оны салымға қою тиімсіз болуы да мүмкін. Сөйтіп, мақсат қорын құрып, ақша-ны инвестрлеудің бірнеше нұсқалары (есепте A, B, C, D (5.4–кесте)) бар екеніне көз жеткізуге болады. Фермер барлық мүмкін бола алатын нұсқалардың (есепте келтірілген нұсқаларды бір–бірімен байланыста қарастырса 60-тан астам жаңа нұсқаларды алуға болады) ішінен ақшаны салымға пайыздық үстемемен қою-дың 12 тәсіліне тоқталды делік. Салым нұсқасы, олардың ұзақ-тығы, салым салу уақыты және пайыздық үстемесі 5.4 және 5.5–кестелерде келтірілген.