 |
|
Тапшысымен тасымалдау есебі 8 страница
5. Қаржылық есептердің модельдері
Тәжірибеде басқа оңтайластыру есептеріне қарағанда жиі байқалатын, көптеген жағдайларда оңтайлы шешім қабылдауды қажет ететін әртүрлі қаржылық есептерін кездестіруге болады. Шындығында, есепті шешу нәтижесінің критериясы максимумге, мысалға, пайда, табыс және тағы басқа немесе минимумге, мысал-ға, өзіндік құн, өнімнің бағасы және тағы басқада көрсеткіштер ізделінетін барлық оңтайластыру есептері, қаржылық есептеріне жатады. Сонымен қатар кәдімгі қаржылық есептерге, шығынсыз-дық (зиянсыздық) нүктені есептеу, капиталды іске салуды жоспар-лау, инвестициялау портфельдерін қалыптастыру, ақша ағымын басқару және басқа да қаржы айналымына байланысты есептерді жатқызады.
Қаржылық есептердің математикалық модельдері сызықтық, сызықты емес, бүтін санды, екілік айнымалылармен және басқа да түрде, сонымен қатар өзінің құрамы бойынша өндірістік, қоспа есебі сияқты, транспорттық типтес, тағайындау есебіне ұқсас және басқа да типте болуы мүмкін. Сонымен қатар, қаржылық есеп-терінің өздеріне тән айрықшылықтары болады. Олардың мағына-сында уақыт анық байқалып тұрады. Мысалға, уақыт бойынша шамалары бірқалыпты емес, капитал салымын жоспарлағанда немесе ақша ағымын басқарғанда пайыздық үстеме есептелінеді. Бірақ осыған қарамастан қаржылық есептер, динамикалық емес, міндетті түрде статистикалық делінеді, яғни басқаша айтсақ, мұндай модельдерде, уақыт тәуелсіз айнымалы емес, әйтеуір бір параметрі ретінде ескеріледі.
Жұмыс барысында қаржылық есептермен кез келген кәсіпкер немесе кәсіпорын жетекшісінің жиі айналысуына тура келетіні сөзсіз. Сондықтан келесі тақырыптарда тәжірибеде жиі кездесетін, біршама қызықты қаржылық есептерін қарастырамыз.
5.1 Шығынсыздықты (зиянсыздықты) талдау
Экономикада шығынсыздықты (зиянсыздықты) талдау ма-ңызды мәселе. Шығынсыздықты талдау барысында, жаңа өндірісті ұйымдастыру үшін, қанша қаржы керектігі бағаланады және жаңа өнімді өндіру үшін іске салынатын капитал туралы жан-жақты талдаулар жасалынады. Жаңа өнімді өндіруге кеткен барлық шығындардың сомасы және оған қосылған бастапқы кезде осы өндірісті іске қосу үшін салынған капитал мөлшері мен өнімді нарыққа шығарып, сатқанда алынған барлық табыстардың сомасы тең болатын уақыт аралығы ізделінеді. Сонымен қанша уақыт мөлшерінде өндіріс шығынсыз нүктеге жететіні, яғни шығын және кіріс тең болатын уақыт анықталынады.
Өнім өндірілмейтін халық шаруашылығының кейбір сала-ларында, мысалға, сауда-сатық салада немесе тұтынушыларға қыз-мет көрсету орындарында шығынсыз нүкте – рентабельдіктің та-балдырығы (орысша - порог рентабельности) деп аталады.
Есептің мағынасы түсінікті және қарапайым болу үшін өнді-рісті іске қосуға салынған алғашқы капитал мөлшері белгілі деп есептейік.
Айталық, бір кәсіпорын n жаңа Б1, Б2,…,Бn деп аталатын бұйымдарды шығаруды жоспарлап отыр делік. Бұйымдардың әр-қайсысын алдын-ала жобаланған шамада шығару үшін в1, в2, ..., вn мөлшерде бастапқы капиталды іске салу керек болсын. Бұл капиталдар бекітілген немесе тұрақты деп аталатын шығындар және олардың шамалары алдыңғы уақыттарда бұйымдардың өндіру мөлшерінің дамуымен байланысы болмайды. Негізінде бұл шығын-дарға, алғашқы құралдарды сатып алуға, оларды жұмысқа қосуға кеткен және т.б. жұмыстар үшін керекті шығындар жатады. Осы шығындармен қатар, өндірісте өнімдер түрлеріне байланысты бөлінбейтін жалпы в0 мөлшерде бекітілген шығын болуы мүмкін. Мысалға, кәсіпорында барлық бұйымдарды өндіруге қатысы бар, жаңа цех құрлысының бағасы (в0) немесе т.б.с.с.
Әрбір жаңа Б1, Б2,…,Бn бұйымдардың бір данасының өзіндік құны (з1, з2, ...,зn) және нарықта қаншадан (с1, с2,...,сn) сатылатыны алдын-ала анықталған деп есептейік. Сөйтіп, шығынсыздықты талдауға керекті деректердің манимальды жиынын атап өттік.
Кәсіпорын Б1, Б2, …, Бn деп аталатын бұйымдарды, белгілі бір уақыт аралығында (бір айда, тоқсанда, жарты жылда немесе бір жылда), x1, x2, ..., xn данадан өндіреміз деп жоспарласа, онда осы өнімдерді өндіруге кеткен барлық шығындардың сомасы (қосылған бастапқы өндірісті іске қосу үшін салынған капитал мөлшері) мен оны нарыққа шығарып сатқандағы барлық табыстардың сомасы тең болатын k уақытты арқылы шығынсыздықтың теңдігі құрылады. Бұл теңдікті былай жазыуға болады:
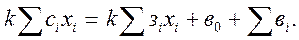
Осы теңдіктен шығынсыз нүктеге жететін уақытты анықтаймыз:
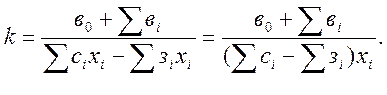
 (5.1)
(5.1)
Сөйтіп, анықталған k мәні бүтін немесе бөлшек сан болуы мүмкін, ал мына сома: 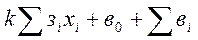 жалпы шығын немесе шығынсыздық нүктесі ізделінетін, өндіріске салынған қаржы мөлшері. Қаржы тілінде өнімді өндіруге кеткен шығындарды k∑зiхi – айнымалы шығындар деп атайды да, ал в0 + ∑вi - тұрақты шы-ғындар делінеді. Осы жерде, шығындарды тұрақты және айнымалы топтарға бөлу, экономикалық талдауларда маңызды мәселе екенін атап өтейік.
жалпы шығын немесе шығынсыздық нүктесі ізделінетін, өндіріске салынған қаржы мөлшері. Қаржы тілінде өнімді өндіруге кеткен шығындарды k∑зiхi – айнымалы шығындар деп атайды да, ал в0 + ∑вi - тұрақты шы-ғындар делінеді. Осы жерде, шығындарды тұрақты және айнымалы топтарға бөлу, экономикалық талдауларда маңызды мәселе екенін атап өтейік.
Негізінде өндірістің мақсаты шығынсыздық нүктедегі өнді-рілетін өнімдердің мөлшерін (x1, x2, ..., xn) анықтау және бұл өндіріс деңгейінде қызықты мәселе. Мұндай жағдайда шығынсыз нүктеге жететін уақыт аралығы бірге теңестіріледі (k=1) де, нәти-жесінде шығынсыздықтың теңдеуін мына түрге айналдырады:

немесе
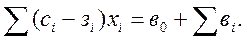 (5.2)
(5.2)
Көп өнімді есептер үшін мұндай теңдеулердің шексіз ше-шімдері болуы әбден мүмкін, ал жалғыз ғана өнімді есептерде бір-ақ шешімі болады. Көп өнімді есептерді шығару үшін қосымша шарттар енгізіледі. Мұндай шарттарда көбінесе шығынсыз нүктеге жеткенге дейінгі айнымалы шығындардың минимальды немесе пайданың максимальды болуын көздейтін, белгісіздердің мәндерін анықтайды.
Есепті аталған мақсаттарда шығаратын болсақ, бірінші жағдайда шығынсыз нүктеге жеткізуге кеткен қаржылық шығын азаяды. Бірақ шығынсыз нүктеге жететін уақыт ұзарады. Екінші жағдайда шығынсыз нүктеге жетуге кеткен уақыт азаяды. Бірақ шығынсыз нүктеге жеткізуге кеткен қаржылық шығын көбейеді.
Оңтайлы өндірістік жоспарды анықтағаннан кейін, осы жоспарды орындау мерзімі сияқты шығынсыздық нүктеге жету мерзімі есептелінеді.
Шығынсыз нүктеге жету үшін, өндірістің оңтайлы жоспары анықталатын есептің математикалық моделін құрамыз. Математи-калық модельді жазуға керекті белгілер толығымен белгілі, атап айтсақ:
– Б1, Б2, …, Бn – бұйымдарының оңтайлы мөлшерлерін көр-сететін: x1, x2, ..., xn – айнымалылары;
– бұйымдардың өзіндік құны (з1, з2, ...,зn) және олардың сатылатын бағалары (с1, с2, ...,сn );
– бұйымдардың әрқайсысын өндіруге қажетті бастапқы ка-питалдар в1, в2, ..., вn –мөлшері және т.б.
Егер өндірістік оңтайлы жоспар құру үшін айнымалы шы-ғындардың минимальды болу шарты қарастырылса, онда мақсат функция мына түрде жазылады:
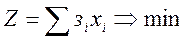 (5.3)
(5.3)
Егер өндірістік оңтайлы жоспар максимальды пайда алу шартына есептелінсе, онда мақсат функция мына түрде жазылады:
 (5.4)
(5.4)
Шектеу ретінде шығынсыздықтың теңдеуі алынады:
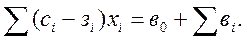 (5.5)
(5.5)
Сонымен есептің математикалық моделін құрдық. Тәжірибе-лік есептерді шығарғанда нақтылы өндірістің жағдайларына байла-нысты басқада шектеулер құрылуы мүмкін. Мысалға, өндіріс қуа-тының немесе қорларының шектеулігіне, қала берді нарық сұра-нысына байланысты жаңадан бірнеше шектеулер қарастыруға болады.
5.1.1 Жаңа ұйымдастырылып жатқан нақтылы өндірістің шығынсыздығын (зиянсыздығын) талдау
Бір мысал қарастырайық. «Димаш» деп аталатын компания жаңадан үш түрлі (А, Б, В) бұйымдарды өндірумен айналыспақшы. Өндірістің бастапқы жағдайындағы экономикалық деректер келесі кестеде келтірілген.
5.1-кесте. Өндірілетін бұйымның бір данасына шаққандағы көрсеткіштер, мың теңге
| Бұйымдар | Бұйымның бір данасының бағасы | Айнымалы шығындар | Бастапқы жалпы шығын |
| А | |||
| Б | |||
| В |
Есепте жалпы шығын (в0) берілмеген, бірақ әрбір бұйымды шығаратын өндіріске керекті бекітілген шығындар белгілі (кестеде соңғы бағанада).
Осыдан кейін «Димаш» компаниясы алдында шығынсыздық нүктеге жеткізетін өндірістік жоспарды анықтау есебі туындалы-нады. Жаңадан құрылатын өндіріс жұмысын бастамас бұрын ком-пания тұтынушыларға өндіретін бұйымдардың қаншалықты қажет-тілігін анықтау үшін нарық жағдайларына маркетингтік зерттеу-лер жүргізді. Нәтижесінде, А бұйымын 310 дана және В бұйымын 200 дана қажет ететін тұтынушылар, сонымен қатар Б бұйымын 350 данадан артық өндіру компанияға тиімсіз екені анықталынды.
Шешу.Есептің математикалық моделін құрамыз. Ол үшін өндірілетін А, Б, В бұйымдарының оңтайлы мөлшерін ха, хб және хв дана деп белгілейік. Шығынсыздықтың теңдеуін тұрғызайық:
75ха + 60хб + 90хв = 40ха + 35хб + 50хв + 7500 +8500 + 6000
немесе түрлендіргеннен кейін:
35ха + 25хб + 40хв = 22000, бұл бірінші шектеу.
Енді маркетингтік зерттеу нәтижесін ескерсек:
ха ≥ 310, хв ≥ 200 және хб ≤ 350.
Айнымалылардың теріс болмау шартын тек хб – айнымалы-сына қоямыз, яғни хб≥0.
Есепті осы тұрғызылған шектеулерде екі мақсат функция-лары бойынша шығарайық. Бірінші мақсат функция максимальды табысты іздеу болсын, яғни:
Z = 75ха + 60хб + 90хв → max.
Есепті шешу нәтижесінде шығынсыздық нүктеге жетуге дейінгі аралықта табысты максимумға іздейтін өндіріс жоспары анықталынады. Екінші мақсат функция айнымалы шығындарды минимумге іздеу, яғни:
Z = 40ха + 35хб + 50хв → min.
Есепте шығынсыздық нүктеге жеткенге дейінгі айнымалы шығындарды минимумге іздейтін өндіріс жоспары анықталынады.
Әрі қарай жоғарыда құрылған математикалық модельдер ар-қылы MS Excel-дің жұмыс бетіне кестелік модель тұрғызамыз. Кестелік модель және бірінші мақсат функцияны максимумге ізде-генде табылған есептің оңтайлы шешімі 5.1-суретте көрсетілген. Көріп отырсыз, қарастырылып отырған есептің кестелік моделінің өндірістік есептердің кестелік модельдерін MS Excel-дің жұмыс бетіне орналастыру тәсілінен онша көп айырмашылығы жоқ.

5.1-сурет. Шығынсыздық модельдің бірінші шешімі
Бірінші мақсат функция мәні D10 ұяшықта 5.1-суретте формулалар жолында көрсетілген формуламен есептелінеді. Екінші мақсат функция мәні D11 ұяшықта суретте көрсетілген формула сияқты формуламен есептелінді. Е14:Е17 аралығындағы ұяларда, шектеулердің сол жағын есептеу үшін =СУММПРОИЗВ – функцияның көмегімен, осы формулаларға ұқсас формулалар қол-данылады.
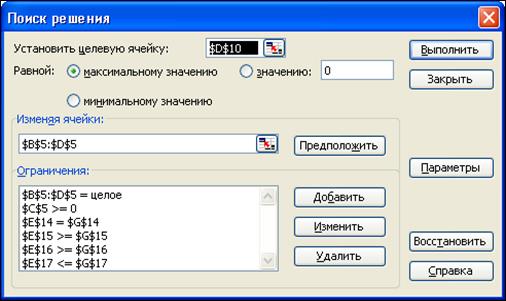
5.2-сурет. Бірінші мақсат функцияны қолданып есепті шешу үшін Поиск решения-ның сұхбаттасу терезесі
Бірінші мақсат функцияны қолданып, есептің шешімін табу үшін Поиск решения-ның сұхбаттасу терезесін 5.2-суретте көрсет-кен қалыпта толтырамыз. С5 ұядағы хб≥0 теріс болмау шартын жазамыз. Басқа айнымалыларға теріс болмау шартын белгілеудің қажеті жоқ. Тек құрылған модель сызықтық екенін және масштаб-тауды автоматты орындау керектігін машинаға түсіндіру үшін оларды белгілеп (флажок қою) кеткен дұрыс.
Есептің бірінші мақсат функция бойынша табылған оңтайлы шешімінен (5.1-суретте), шығынсыздық нүктеге тез арада жету үшін 310 дана А бұйымын, 126 дана Б бұйымын және 200 дана В бұйымын өндіру керек. Осы нүктеге жеткен мерзімде жалпы табыс 48810 мың теңге болса, ал айнымалы шығын 26810 мың теңге құрайды.
Есепті екінші мақсат функция арқылы шешу үшін Поиск решения-ның сұхбаттасу терезесі 5.3-суретте көрсеткен қалыпқа келтіріледі. Бұл терезедегі нұсқалардың алдыңғы 5.2-суреттегі те-резеден айырмашылығы мақсаттық ұяшық $D$11 және оның ба-ғыты басқаша.
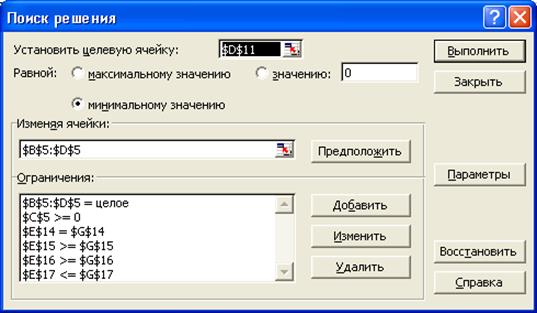
5.3-сурет. Екінші мақсат функцияны қолданып есепті шешу үшін Поиск решения-ның сұхбаттасу терезесі

5.4-сурет. Шығынсыздық модельдің екінші шешімі
Екінші мақсат функция бойынша табылған шешім 5.4-сурет-те көрсетілген. Көріп отырмыз, жаңа шешімде Б бұйымды өндіру жалпы қарастырылмайды, яғни өндірістік жоспар бұл шешімде алдыңғы шешімнен нашар. Бірақ табыс 810 мың теңгеге кемісе, айнымалы шығындар да бірінші шешімге қарағанда осынша шамаға (26810-26000 = 810 мың теңге) кеміген, яғни пайда екі шешімде де бірдей.
Теориялық жағынан шығынсыздық нүктеге жету мерзімі, бірінші шешімде қысқа болатыны дәлелденді, сонымен қатар барлық қабылданған бұйымдарды өндіру қарастырылуына байла-нысты бірінші шешім тиімді деп санаймыз. Сондықтан «Димаш» компаниясы өндірістің бірінші жоспарын қабылдайды. Сөзсіз, бұл тұжырым ең соңғы емес және өндірістің жалпы тиімді болуын қарастыру біздің есептің мақсатына жатпайды.
5.2 Инвестициялық жобаларды таңдау есебі
Тәжірибеде өндірісте бірнеше жаңа өндіріс орындарында қоғамға пайдалы әртүрлі жаңа өнім өндіру, қызметтер және т.б. іс-әрекеттер жасау үшін жобалар жасалынады. Ал оларды іске асыру үшін бастапқы қаражаттар қажет екені әркімге белгілі. Міне осын-дай істерге бүгінгі нарық заңдылықтары бойынша инвестр деп аталушы ақшалы адам, ақшасын іске салады (инвестициалау делі-неді), яғни ақшасын іске жұмсайды да, табыс табады.
Инвестициялық жобаны таңдау ұғымын терең түсіну мақса-тында бір қарапайым есепті қарастырайық. Мысалға, жалпы m кезеңдерде (ай, тоқсан, жарты жыл, жыл) n инвестициялық жоба-ларды (П1, П1, ..., Пn) іске асыру керек делік. Әрбір кезеңнің басында әрбір жоба қажетті нақтылы сомамен инвестициялануға тиісті, ал пайда m – ші кезеңнің соңында есептелінетін болсын. Осы аталған деректерді кестеде келтірген ыңғайлы (5.2-кестені қараңыз).
Кестеде Сij – j-шы кезеңнің басында Пi – жобаны инвести-циялау сомасы (осы жобаға қажетті қаражат мөлшері); Dі – Пi – жобаны іске қосу нәтижесінде m-ші кезеңнің соңында күтілетін пайда немесе таза табыс; Sj – j-шы кезеңнің басындағы инвестрдің мүмкіндігі, яғни кез келген инвестрдің қаржысы шектеулі, сон-дықтан әрбір кезеңде оның қаржысы барлық жобалардың қажетілік сомасынан аспайды. Сонымен, инвестициялау қорының шектеулі жағдайында инвестр максимальды табыс түсіретін жобаларды таң-дау керек.
5.2-кесте. Инвестициялық жобалар туралы деректер
| Жобалар | Әрбір кезеңнің басында инвестициялау қажеттілігі | Күтілетін пайда | |||
| 1-ші кезең | 2-ші кезең | ... | m-ші кезең | ||
| П1 | С11 | С12 | … | С1m | D1 |
| П1 | С21 | С22 | … | С2m | D2 |
| ... | … | … | … | ||
| Пn | Сn1 | Сn2 | … | Сnm | Dn |
| Инвестрдің мүмкіншілігі | S1 | S2 | … | Sm |
Қойылған есептің математикалық моделін құрамыз. Ол үшін мынадай жағдайларды негізге аламыз. Айталық, инвестр өзінің қалауы бойынша жобаны іске асыруға толық қатысуды міндет-тенуі (сөзсіз, егер ол оны таңдап алса) немесе міндеттенбеуі (егер ол оны таңдап алмаса) немесе үлеспен инвестициялауға келісуі мүмкін. Осы баяндалған ситуацияларды модельде ескеру үшін айнымалы-ларды 1-ші және 2-ші типтерге бөледі, ал айнымалылар типтері мынадай шарттарға байланысты анықталады.
Бірінші жағдайда х1, х2, ..., хn екілік айнымалылар енгізіледі. Бірінші шарт, егер инвестр i-жобаны таңдап алса, онда ол жобаның сұранысын толық қанағаттандырады (хi=1), i-ші жобаны таңдамаса (хi=0). Мұндай айнымалыларды 1-ші типтік бульдік (екілік) айнымалылар деп атайды.
Екінші жағдайда х1, х2, ..., хn сәйкес жобаларға инвестрдің қатысу үлесін көрсетеді. Егер инвестр i-жобаны толық қанағатан-дырмай, тек оған өз үлесімен ақша салатын болса, онда хi – 0-ден 1-ге дейін үздіксіз өзгеретін шамаға айналады да, оны 2-ші типтегі айнымалылар деп атайды. Ескерту: Екінші шарт жағдайында инвестрге түсетін пайда, оның жобаға үлестік қатынасына байла-нысты есептелінеді.
Математикалық модельде айнымалыларды жоғарыда баян-далған типтерге бөлу, мақсат функцияны және шектеулердің фор-мулаларының мағынасын өзгерпейді.
Есептің мақсаты максимальды табыс әкелетін жобаларды таңдау болғандықтан, мақсат функция мына түрде жазылады:
Z = ∑Dixi → max (5.6)
Әрбір j- кезеңдерде инвестициялау сомасы инвестрдің осы кезеңдегі мүмкіндігінен көп болмайды:

(5.7)
Егер кейбір кезеңдерде инвестициялайтын сомаларға шектеу-лер жоқ болса, онда осы кезеңдерге шектеулер қойылмайды. Осы шектеулерден басқа керекті шарттар:
– бірінші типтік айнымалылар үшін екілік болу шарты;
– теріс болмау шарты және екінші типтік айнымалылар үшін х1 ≤1, х2 ≤1, ..., хn≤1.
Екінші типтік айнымалылар көмегімен қосымша жобалар топтарын таңдау шарты жай қарапайым түрде іске асырылады. Мысалға, егер П1, П1 және П3 жобалар тобынан шарт бойынша біреуі (немесе біреуі де емес) таңдалынса, онда бұл шарт, шектеу түрінде былай жазылады: х1+х2+х3 ≤1. Тағы да басқа бір мысал. Айталық, П5 жобаны тек П4 жоба қабылданған жағдайда таңдайды делік, онда ол мына шарт: х4 – х5 ≤ 0 арқылы іске асырылады.
Сонымен, жалпы инвестициялық жобаларды таңдау ситуация-ларының біразі қаралып, оларды ескеру үшін математикалық мо-дель құру тәсілдері баяндалды. Тәжірибеде басқа бір ситуациялар кездескен жағдайда осы баяндалған тәсілдерге сүйеніп, мақсатқа жететініңізге сенімдіміз.
Келесі тақырыпта жоғарыдағы баяндалған тиімді инвестиция-лық жобаларды таңдау әдістерімен нақтылы есептерді MS Excel-де шығару тәсілдері қарастырылады.
5.2.1 Қаржылық қорларды активтендіру үшін инвестициялық жобаларды таңдау есептерін MS Excel-де шығару тәсілдері
«Димаш» компаниясы бос қаржысын іске қосып пайда табу үшін инвестицияланатын жобалар таңдамақшы. Компанияға, әр-түрлі өнім өндірумен айналысатын 5 жобаларға, ақша салуға (жобаларды инвестициялауға) ұсыныс жасалынды. Осы жобалар-дың қаншасын және нақтылы қанша, қандай жобаларға ақшаны іске салғанда, компанияға көп пайда түсіретіндерін таңдау қажет. Ұсы-нылған жобалар туралы деректер 5.3-кестеде берілген.
5.3-ші кесте. Жобалардың қаржылық көрсеткіштері
| Жобалар | Әрбір тоқсанның басында инвестициялау, мың тенге | Күтілетін пайда, мың теңге. | |||||
| 1-ші тоқсан | 2-ші тоқсан | 3-ші тоқсан | 4-ші тоқсан | 5-ші тоқсан | 6-шы тоқсан | ||
| П1 | |||||||
| П2 | |||||||
| П3 | |||||||
| П4 | |||||||
| П5 | |||||||
| Инвестрдің бос қаржысы, мың тенге |