 |
|
Тапшысымен тасымалдау есебі 10 страница
Кестедегі келтірілген деректер бойынша құралдың құнын төлеуді қамтамасыз ететін мақсаттық қордың мөлшерін мини-мальдау керек.
Сөйтіп, мынадай сұрақтар туады:
– құралдың толық құнын шартта көрсетілген уақытта төлеуді қамтамасыз ететін мақсаттық қордың мөлшері қанша болуы тиіс?
– уақыт мезгілінің бас кезінде, жетінші айдың басында (6–ай біткеннен кейін) төленетін ақшаның бір теңгесінің бағасы қанша?
– уақыт мезгілінің бас кезінде, бесінші айдың басында (4–ай біткеннен кейін) төленетін ақшаның бір теңгесінің бағасы қанша?
5.5–кесте. Салым салу және қаражатты қайтару мүмкіндіктері туралы деректер (үлестік коэффициенттері)
| Салым | Айлар (осы айлардың бірінші күні) | ||||||
| А, 1–айда | 1,00 | 1,015 | |||||
| А, 2–айда | 1,00 | 1,015 | |||||
| А, 3–айда | 1,00 | 1,015 | |||||
| А, 4–айда | 1,00 | 1,015 | |||||
| А, 5–айда | 1,00 | 1,015 | |||||
| А, 6–айда | 1,00 | 1,015 | |||||
| В, 1–айда | 1,00 | 1,035 | |||||
| В, 3–айда | 1,00 | 1,035 | |||||
| В, 5–айда | 1,00 | 1,035 | |||||
| С, 1–айда | 1,00 | 1,06 | |||||
| С, 4–айда | 1,00 | 1,06 | |||||
| D, 1–айда | 1,00 | 1,11 |
Ескерту: Кестеде жолдар бойынша бір нүсқада ақшаны пайыздық үстемеге салу (коэффициенті 1,00 тең) және қайтару (коэффициенті, пайыздық үстеме (5.4–кестені қараңыз) және қосылған бір) әрекеттердің коэффициенттері келтірілген.
Шешімі. Келесідей белгілерді енгізейік:
y – мақсаттық қордың мөлшері;
xAi – i-айында салынатын А-нұсқасындағы салым мөлшері;
xBi – i- айында салынатын B-нұсқасындағы салым мөлшері;
xCi – i- айында салынатын C-нұсқасындағы салым мөлшері;
xDi – i- айында салынатын D-нұсқасындағы салым мөлшері;
Ақшаны қолда сақтау ешқандай да пайда түсірмейді, сон-дықтан қолға ақша түссе кез келген айда оны пайыздық үстемемен іске саламыз. Осы жағдайды ескеріп және 5.5–кестедегі деректер бойынша мақсаттық қорды минимальдау есебінің моделі төмен-гідей түрде жазылады:
Мақсат функция
Мына жағдайда:
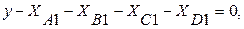
Тұрғызылған модельді матрица кестесіне (5.6–кестеге қара-ңыз) жазып, есепті компьютерде шығарайық.
Есептің компьютерде алынған нәтижесінен (5.6–кесте) мына көрсеткіштердің оңтайлы мәндерін анықтадық:
– минимальды мақсаттық қор y = 678 925,4 теңге, яғни құралдың толық құнын шартта көрсетілген уақытта төлеуді қам-тамасыз ететін мақсаттық қордың мөлшері;
– A – нұсқасы бойынша бірінші ай басында салымға ақша Xa1= 0, салу тиімсіз;
– B – нұсқасы бойынша бірінші ай басында салымға Xb1=144 927,5 теңге ақша салған пайдалы, яғни тиімді;
– C – нұсқасы бойынша бірінші ай басында салымға Xc1=533 997,8 теңге ақша салу пайдалы, яғни тиімді және т.б. с.с.
5.15–сурет. Сандық экономикалық–математикалық модельдің шешімі
5.6–кесте. Есептің компьютерде алынған нәтижесі
| Целевая ячейка (Минимум) | ||||||
| Ячейка | Имя | Исходное значение | Результат | |||
| $O$9 | Минимум | 678,9254002 | 678,9254002 | |||
| Изменяемые ячейки | ||||||
| Ячейка | Имя | Исходное значение | Результат | |||
| $B$10 | у | 678,9254002 | 678,9254002 | |||
| $C$10 | Xa1 | |||||
| $D$10 | Xb1 | 144,9275362 | 144,9275362 | |||
| $E$10 | Xc1 | 533,997864 | 533,997864 | |||
| $F$10 | Xd1 | |||||
| $G$10 | Xa2 | |||||
| $H$10 | Xa3 | |||||
| $I$10 | Xb3 | |||||
| $J$10 | Xa4 | |||||
| $K$10 | Xc4 | 566,0377358 | 566,0377358 | |||
| $L$10 | Xa5 | |||||
| $M$10 | Xb5 | |||||
| $N$10 | Xa6 | |||||
| Ограничения | ||||||
| Ячейка | Имя | Значение | Формула | Статус | Разница | |
| $O$2 | 1–ай басы | 1,13687E–13 | $O$2=$Q$2 | не связан. | ||
| $O$3 | 2–ай басы | $O$3=$Q$3 | не связан. | |||
| $O$4 | 3–ай басы | $O$4=$Q$4 | не связан. | |||
| $O$5 | 4–ай басы | $O$5=$Q$5 | не связан. | |||
| $O$6 | 5–ай басы | $O$6=$Q$6 | не связан. | |||
| $O$7 | 6–ай басы | $O$7=$Q$7 | не связан. | |||
| $O$8 | 7–ай басы | $O$8=$Q$8 | не связан. |
5.7–кесте. Мақсат функция коэффициенттерінің орнықтылығы
| Изменяемые ячейки | ||||||||
| Результ. | Нормир. | Целевой | Допустимое | Допустимое | ||||
| Ячейка | Имя | значение | стоимость | Коэффициент | Увеличение | Уменьшение | ||
| $B$10 | у | 678,9254002 | 1E+30 | |||||
| $C$10 | Xa1 | 1E+30 | 0,004613523 | |||||
| $D$10 | Xb1 | 144,9275362 | 0,004634906 | 0,004345202 | ||||
| $E$10 | Xc1 | 533,997864 | 0,004364165 | |||||
| $F$10 | Xd1 | 0,012103947 | 1E+30 | 0,012103947 | ||||
| $G$10 | Xa2 | 0,004545343 | 1E+30 | 0,004545343 | ||||
| $H$10 | Xa3 | 0,008636407 | 1E+30 | 0,008636407 | ||||
| $I$10 | Xb3 | 0,004198263 | 1E+30 | 0,004198263 | ||||
| $J$10 | Xa4 | 0,004117137 | 0,008432712 | |||||
| $K$10 | Xc4 | 566,0377358 | 0,008508769 | 1E+30 | ||||
| $L$10 | Xa5 | 1E+30 | 0,012557827 | |||||
| $M$10 | Xb5 | 0,00830809 | 1E+30 | 0,00830809 | ||||
| $N$10 | Xa6 | 0,012372244 | 1E+30 | 0,012372244 | ||||
| Ограничения | ||||||||
| Результ. | Теневая | Ограничение | Допустимое | Допустимое | ||||
| Ячейка | Имя | значение | Цена | Правая часть | Увеличение | Уменьшение | ||
| $O$2 | 1-ай басы | 1,1367E–13 | 1E+30 | 678,9254002 | ||||
| $O$3 | 2-ай басы | 0,985221672 | 1E+30 | |||||
| $O$4 | 3-ай басы | 0,966183575 | 1E+30 | |||||
| $O$5 | 4-ай басы | 0,943396226 | 1E+30 | 566,0377358 | ||||
| $O$6 | 5-ай басы | 0,929454408 | 1E+30 | |||||
| $O$7 | 6-ай басы | 0,915718628 | 1E+30 | |||||
| $O$8 | 7-ай басы | 0,88999644 | 1E+30 | |||||
5.8–кесте. Шектеулердің оң жақтарының орнықтылық аралықтары
| Целевое | |||||||||
| Ячейка | Имя | Значение | |||||||
| $O$9 | Минимум | 678,92540 | |||||||
| Изменяемое | Нижний | Целевой | Верхний | Целевой | |||||
| Ячейка | Имя | Значение | предел | результат | предел | результат | |||
| $B$10 | у | 678,92540 | 678,92540 | 678,92540 | 678,92540 | 678,92540 | |||
| $C$10 | Xa1 | 678,92540 | 678,92540 | ||||||
| $D$10 | Xb1 | 144,927536 | 144,927536 | 678,92540 | 144,92753 | 678,92540 | |||
| $E$10 | Xc1 | 533,997864 | 533,997864 | 678,92540 | 533,99786 | 678,92540 | |||
| $F$10 | Xd1 | 1,024E–13 | 678,92540 | 1,024E–13 | 678,92540 | ||||
| $G$10 | Xa2 | 678,92540 | 678,92540 | ||||||
| $H$10 | Xa3 | 678,92540 | 678,92540 | ||||||
| $I$10 | Xb3 | 678,92540 | 678,92540 | ||||||
| $J$10 | Xa4 | 678,92540 | 678,92540 | ||||||
| $K$10 | Xc4 | 566,037735 | 566,037735 | 678,92540 | 566,03773 | 678,92540 | |||
| $L$10 | Xa5 | 678,92540 | 678,92540 | ||||||
| $M$10 | Xb5 | 1,098E–13 | 678,92540 | 1,098E–13 | 678,92540 | ||||
| $N$10 | Xa6 | 1,120E–13 | 678,92540 | 1,120E–13 | 678,92540 |
Модельде қосалқы бағаның түсіндірмесі өте қызықты. Мы-салы, соңғы шектеудің қосалқы бағасы 0,8899 тең (5.7–кестені қараңыз). Осы мән, жарты жылдан кейін бір қосымша теңгені өтеу үшін, мақсаттық қордың мөлшерін 0,8899 теңгеге көбейту керек-тігін білдіреді. Сонымен, қосалқы бағаның шамасы, жарты жылдан кейін төлейтін, уақыттың басқы мезгіліне келтірілген бір теңгенің бағасын көрсетеді.
Есептің шарты бойынша уақыт мезгілінің бас кезінде, жетін-ші айдың басында (6–ай біткеннен кейін) төленетін ақшаның бір теңгесінің бағасы 0,8899 теңге және бесінші айдың басында (4–ай біткеннен кейін) төленетін ақшаның бір теңгесінің бағасы 0,929 теңге болатындығы анықталды.
5.4 Нақтылы кәсіпорын мен қаржылық институт арасындағы несиелік байланыс желісін модельдеу
Республикамызда қазақстандық микро бизнестік бағдарлама (ҚМББ) ауылшаруашылығына несие беруде кеңейтіліп және табыс-ты дамуда. Қазіргі кезде Қазақстан Республикасы бойынша ҚМББ 200 ден астам несие беруші секторлары мен филиалдары қызмет етуде және олардың қысқа мерзімде ауылшаруашылығына несие беруді дамытуға мүмкіншіліктері жетерлік. Бірақ ауылшаруа-шылығының қарызгерлері алдында инвестерлермен осындай байланысты дамытуда біраз шешілмеген мәселелер кездеседі. Осы мәселе бойынша несиені уақытында алу және оны тиімді қолдану тактикаларын шешуде несиелік байланыстарды модельдеу арқылы несие беруші мен қарызгер байланыстарын (желісін) оңтайластыру қажеттігі туындайды.
Мерзімдік және уақыттық түрленген кесінділерде ақша ағымына мониторинг жүргізу нәтижесінде, ақша қаражаттар қоз-ғалысын кәсіпорынның шотында кіріс және шығыс бөліктері бойынша несиені алуды және оны уақыттылы төлеуді ұйымдасты-руға, сонымен қатар жалпы жұмысты тиімді басқаруды оңтайлас-тыруға мүмкіндік туады. Берілген пайыздық үстемесімен несиелік байланыс желісін модельдеу арқылы ауыл шаруашылық кәсіп-орынның өнім ағымдары құрамдарының және қорларының өзгеріс-теріне байланысты несиені алатын тиімді мерзімді және оны тиімді өтейтін уақытты анықтауға болады. Модельде несиені беру шарт-тары бойынша (мысалға, ақша қаражаттарының займы), әртүрлі параметрлерімен бірнеше несиелік байланыс сызықтары қарасты-рылса, онда компьютерде модельдеудің нәтижесінде солардың ішінен ең қажеті және тиімдісін таңдай аламыз және әртүрлі қар-жылық, сонымен қатар кәсіпорынның өндірістік жағдайларында керекті параметрлерді (мысалға, төлем пайызын, несиені қайтара-тын мерзімнің ұзақтығын және т.б.) оңтайластыруға болады.
Несиелік байланыс желісін модельдеу үрдісін, агроөнеркәсіп-тік кешені кәсіпорынның іс–қимылының экономикалық–математи-калық есебін модельдейтін өз бетінше бөлек блогы ретінде қарас-тырайық.
Есептің жалпы математикалық тілде қойылуы – тағайындал-ған уақыт арылығында несиеге қаражатты алу және оны қайтару жоспарын құруда келесідей шарттарды анықтау қажет деп тұжы-рымдайық:
Þ несие үшін берілген пайыздық үстемені есептеу;
Þ несиені пайызымен қоса міндетті түрде өтеу;
Þ несие бойынша ағымдағы қарыз сомасын анықтау;
Þ қаражатты кәсіпорында нәтижелі тиімді қолдану мақса-тында уақыт бойынша теңестірілген ақша ағымын қаматамасыз-дандыру.
Келтірілген шарттармен қатар несие алу және өтеу әрекет-терінің тиімді мерзімін таңдау әрекеті жалпы математикалық мо-дельде ескерілуге тиіс. Сөйтіп, қойылған шарттар тәжірибеде бола-тын барлық жағдайларды, өндіріс өзгерістерін және несиеге беру-ші мен өнім өндіретін кәсіпорынның нақтылы байланыстарын қамтитын модель құру арқылы және ақпараттық технологиямен кейіптеу негізінде анықталады.
Банктің кәсіпорынына несие беру және кәсіпорынның банк-пен әрекетін біріктіріп бір блок ретінде қарап, несиелік байланыс желісін кәсіпорынның іс–қимылының экономикалық–математика-лық моделі түрінде қарастырсақ және кәсіпорында ақша ағымын айрықша бейнелеп, өндірісте болатын барлық жағдайларды зерт-теп, нәтижесінде несиелік байланыс желісін оңтайластырамыз.
Несиелік байланыс желісін модельдеуші блок, айрықша қа-былданған айнымалылардың ішкі жүйесінен және қаржылар ағымы арқылы жалпы жүйемен байланысқан шектеулерден тұрады. Нақ-тылы несиелік байланыс желісі бойынша айнымалылар жүйесі, уақыт аралығының басында алынған қаражаттар сомасын көрсете-тін және аралықтың аяғында қалған қарыздарды бейнелейтін айнымалылар топтары, сонымен қатар берілген уақытта несие үшін төленетін, үстемесін есептеп қосылатындарды көрсететін, кез келген уақыт аралығында несие үшін төленген және қорытынды төлемді көрсететін айнымалылардан құралады. Несиелік байланыс желілерінің блогы мен экономикалық–математикалық іс–әрекеттік модельдің айнымалар жүйесін бір–бірімен байланыстыру үшін, сонымен қатар несиелік байланыс желісі бойынша модельді шешуде өз бетінше байланыстырушы қосымша блок ретінде, айнымалылардың құрамына, қарастырылатын уақыттың бір мезгі-лінде келетін қаражатқа, шығындарға және ұлғайып отыратын бос, еркін қаражаттар үшін қосымша айнымалылар енгізіледі.
Несиелік байланыс желісін модельдеуші шектеулер жүйесінің блогы, пайыздық үстемесімен қоса несиені алу және өтеу әрекет-тері бойынша ақша қаражаттарының қозғалысын өрнектейді және мына көрсеткіштерді есептеуден тұрады:
– уақыт аралығының аяғында несие бойынша қарыз сомасын;
– әрбір аралықта несие үшін төлеу мөлшерін есептеп қосу;
– модельдеу мерзімі бойынша несие үшін төлем мөлшерін
тиімді бөлу;
– несие үшін төлем мөлшерін анықтау;
– несиені өтеу міндеттері, яғни соңғы аралықта қарыз сомасы нөлге тең;
– несиені өтеу мерзімі ұзартылуы мен пайыздарды есептеу әрекетінің тиімді байланыстары;
– құрамды немесе іс–әрекеттік модель блоктарында ақша қаражаттарының ағымын кәсіпорынның шотына енгізу арқылы кейіптеу;
– несиені өтеу тәсілдері (аннуитенттік өтеу немесе мерзімін асырып өтеу) несиені өтеу механизіміне және пайыздарды есептеп қосуға байланысты анықталады.
Несиелік байланыс желісі блогының фрагменттік математи-калық моделі төмендегідей түрде жазылады:
1) Қарастырылып отырған аралықтың соңында қарыздарды анықтау
– 
+ 
– 
+ 
= 
, 
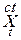(5.18)
немесе
, 
,(5.19)
мұндағы t – ай нөмірі (аралықтағы);
ct – инвестициялық жоба мерзімінің ұзақтығы;
t’ – несиелік желіні қалыптастыру үшін екі аралықтағы айдың нөмірі (аралықтағы);
T – (аралықтағы) айлар нөмірлерінің көптігі;
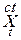– t – айдың (аралықтағы) басында алынған несиенің тиімді мөлшері;
– t – айдың (аралықтағы) соңында несиені қайтарған (өтеген) тиімді мөлшері;
– t – айда (аралықтағы) несие үшін есептелген төлем;
– t – айда (аралықтағы) несие үшін төлем;
–t – айда (аралықтағы) несие бойынша қарыз мөлшері.