 |
|
Тапшысымен тасымалдау есебі 14 страница
Егер біз осы шектеуді модельден алып тастасақ, онда бар-лық инвестиция тұрғын үйлер салуға несиеге беріледі. Айтылған тұжырымды тексеруді оқушының өзіне жүктейміз, ол үшін екінші шектеуді есептің шартынан алып тастаңызда, есепті компьютерде MS Excel “Поиск решения” көмегімен қайта шығарыңыз.
6. Шешімдер қабылдау теориясының негізі
Адамдарға күнде шешімдер қабылдауға тура келеді. Мысал-ға, сіз үйден шығар кезде, қол шатырды алып шыққаным дұрыс па? Жоқ ыңғайсыз бола ма? – деп ойланасыз. Айталық, егер ауа райы жақсы, күн жаумайтын болса, онда сізге қол шатырмен жүру, бір шама ыңғайсыз. Бірақ, жауынды күні қол шатыры, сізге су өтіп кетпеу үшін өте қажетті. Сөйтіп, қол шатырын аласыз ба немесе алмайсыз ба?
Егер ауа райының қандай болатынын алдын-ала білген бол-саңыз бұл сұраққа жауап беру қиын емес. Егер таңертеңнен бастап жауын жауып тұрса, онда сіз, сөзсіз, қол шатырын пайдаланасыз, ал егер жауын біраз уақыттардан кейін тоқтаса, сізге қол шатырын көтеріп жүруге тура келеді. Кейбір адамдар қол шатырын алып жүруді ыңғайсыз санап, көп жағдайларда жауын жауатынын білген күннің өзінде, оны қолына ұстамайды, яғни ауа райы қандай болған күннің өзінде әрбір адамның қолшатыр және оның әсері жөнінде көзқарасы бірдей болмайды. Осы көзқарастар әртүрлі шешімдер тудырады.
Егер қандай ауа райы күтілетіні туралы нақтылы мәлімет болмаса, онда шешім қабылдау қиын да күрделі болады. Ауарайы болжамына да көп сене беруге болмайды. Егер ауа райы туралы болжау мәліметтерін білмесеңіз, онда сіз одан да қиын жағдайға ұшырайсыз.
Сонымен экономикалық объектінің іс-әрекеті және дамуы туралы басқару шешімдерін қабылдауда сыртқы ортаның маңызды сипаттамасы – анықталмағандығын ескеру керек.
Анықталмаған болып, құбылыс, үрдіс, объект туралы ақ-параттың жоқ болуы, толық еместігі, оның жетіспеушілігі немесе ақпараттың дұрыстығы сенімсіз болған жағдайлар түсініледі. Нарық жағдайларында бірдеңенің әсерінен толып жатқан әртүрлі экономикалық объектілер туралы толық мәлімет анықталмаған кездейсоқ жағдай пайда болады. Біздің ойымызша бұл жерде олар туралы мысал келтірудің қажеті болмас.
Нақтылы ақпараттар жоқ жағдайда шешімдер қабылдау әдістерінің мүмкін бола алатын әсерлері тәуекелдік (орысша риск делінеді) теориясы арқылы оқылып, зерделінеді. Қазіргі кезде бұл теория нарық экономикасында кеңінен қолданыс тапқан. Солардың ішіндегі ең маңыздысы – инвестициялық жобаларды таңдау.
Сіздердің назарларыңызға ұсынылып отырған бөлімді оқып, зерделеу барысында мынадай ұғымдарды түсініп, экономикалық талдауларда қолдану тәсілдерін және олардың мәндерін анықтау үшін есептеу әдістерін үйреніп, меңгеруге тура келеді:
– альтернативтер (стратегиялар, шешімдер түрлері, нұсқа-лары);
– ортаның қалыптары;
– шешімдер кестесі;
– шешімдер ағашы;
– талғаусыз (безразличия) критериясы;
– үміттілік (оптимизм) критериясы;
– түңілушілік (пессимизм) критериясы;
– альтернативтерді бағалауда күтілетін (ожидаемая) баға;
– нақтылы ақпараттардың күтілетін құндылығы.
Сонымен қатар, сіздер тәуекелділік, анықталған және анық-талмаған жағдайларда шешімдер қабылдау тәсілдерінің негізін оқып, зерделеп, олар туралы алғашқы түсініктер аласыздар.
Осы жерде кітаптың алдыңғы бөлімдеріндегі модельдер алғашқы мәліметтер толық белгілі және есептердің шартты анық-талған жағдайда қалыптастырылғанын және олар арқылы қабыл-данған шешімдер нақтылы ақпараттарға негізделгенін білген-деріңіз жөн.
6.1 Шешімдер қабылдау модельдері
Шешімдер қабылдау теориясы – аналитикалық тұрғыдан қарағанда көп нұсқалар ішінен ең үйлесімді альтернативтерді (стратегияны, шешім нұсқасын) таңдау немесе бір ретпен әрекет-теу. Шешімдер қабылдау теориясы негізінде үш деңгейде жікте-леді және олар, шешімдер қабылдайтын адамға (ШҚА) кездесетін және оның алдынан шығатын, мүмкін бола алатын алғашқы дерек-тердің анықталу дәрежелерімен немесе солардың әсерімен тығыз байланысты.
Жіктелу деңгейлеріне сәйкес шешімдер қабылдау модель-дерін үш типке бөледі:
1. Анықталған жағдайда шешімдер қабылдау – ШҚА кезкелген альтернативтің бастапқы жағдайын және кейінгі әсерін немесе шешімді қабылдау үшін нелерді ескеріп, таңдау керектігін нақтылы біледі. Мысалға, ШҚА ағымдағы есеп-шотқа салған 100 миллион теңге салым ақша балансын 100 мың теңгеге өсіретінін анық сенімде білетін болса.
2. Тәуекелділік жағдайда шешімдер қабылдау – ШҚА бастапқы жағдай неден басталатынын, оның ықтималдылығын немесе олардың әрбір кейінгі шешімдерге әсерін біледі. Мысалға, біз ертең жауын болатынын да және болмайтынын да білеміз. Мысалға, жауын болатын жағдайдың ықтималдығы 0,3 тең болса, онда оның болмайтын ықтималдығы 0,7 тең екені белгілі.
3. Анықталмаған жағдайда шешімдер қабылдау – ШҚА күтілетін жағдайдың кейінгі әрбір шешімдерге әсерін, бастапқы жағдай неден басталатынын және олардың ықтималдылығын біл-мейді. Мысалға, биылғы жылы шаруашылықта керекті мөлшерде жем-шөп қоры толық жиналынатыны немесе жиналынбайтыны, ШҚА белгісіз болса.
6.1.1 Толық анықталған жағдайларда
шешімдер қабылдау
Зерттелініп отырған құбылыстың немесе үрдістің математи-калық модельдері, сыртқы ортаның қатаң берілген жағдайларында әрбір салыстыратын стратегияларға есептелген жүйенің нәтижелік іс-әрекетінің жекеленген критерияларының мәндері кесте түрінде берілуі мүмкін. Қарастырылып отырған жағдайлар үшін шешімдер қабылдау бір критериямен немесе бірнеше критериялармен жүргі-зілуі мүмкін.
Мысал. Бір фирмаға жаңа өндіріс орнын жабдықтармен қамтамасыздандыру мақсатта оңтайлы стратегия (яғни шешім) қабылдау қажет. Тәжірибелік зерттеулер жүргізу арқылы үш зауытта жасалынатын әрбір жабдықтардың іс-әрекеттерінің жеке-ленген нәтижелілігі (aij) анықталды делік. Бұл жерде «нәтиже-лілік» жалпы атау, ол нақылы жағдайда табыс, пайда, шығыс немесе шығын ұғымдары болуы мүмкн. Осы мәліметтер төменде кестеде келтірілген, яғни экономикалық объектінің алғашқы мәлі-меттері толық анықталған және олар оңтайлы стратегияны таңдау үшін қажет.
Сонымен қатар эксперттердің бағалауымен жекеленген критериялардың µj, 
салмақтары да анықталынған делік, яғни:
µ1= 0,4: µ2= 0,2: µ3= 0,1: µ4= 0,3:
| Жабдықтар (шешімдер стратегиясы) | Жабдықтардың нәтижелілігінің жекеленген критериялары | |||
| Өндірушілігі, а.ө.б. | Жабдықтың бағасы, а.ө.б. | Энергосиым- дылығы, ө.б. | Сенімділігі, ө.б. | |
| 1-зауытта х1 | a11= 5 | a12= 7 | a13= 5 | a14= 6 |
| 2-зауытта х2 | a21= 3 | a22= 4 | a23= 7 | a24= 3 |
| 3-зауытта х3 | a31= 4 | a32= 6 | a33= 2 | a34= 4 |
Ескерту: ө.б. – шартты өлшем бірлігі; а.ө.б – ақша өлшем бірлігі
Есепте оңтайлы стратегияны (жабдық өндіру нұсқасын) бір критерия бойынша таңдау ешқандай қиындық туғызбайтыны бел-гілі. Мысалға, егер жабдықты сенімділігі бойынша таңдайтын болсақ, онда 1-ші зауытта жасалынған жабдықтар ең ұтымды (яғни
х1 стратегия қабылданады).
Оңтайлы шешім бірнеше критериялар арқылы қабылданыла-тын болса (біздің мысалда 4 критериялармен), онда есеп көп-критериялды делінеді.
Көпкритериялы есептерді шешу технологиясы жалпыланған функция Fi(ai1; ai2; …; ain) құрумен байланысты. Жалпыланған функция құру процедурасы критерияларды орау әдісі деп ата-лады. Ораудың бірнеше тәсілдері бар, мысалы:
– аддитивтік оңтайлау әдісі;
– көп мақсатты оңтайлау әдісі және т.б.
Аддитивтік оңтайлау әдісін кеңірек қарастырайық.
Айталық,
(6.1)
Сонымен (6.1) өрнегі аддитивтік оңтайластыру критериясын анықтайтын жалпыланған мақсат функция делінеді. Мұндағы µj салмақ коэффициенттері, яғни j-критериясының маңыздылығы. Басқа критерияларға қарағанда маңызды критерияға үлкен салмақ беріледі және барлық критериялардың жалпы маңыздылығы бірге тең болуға тиіс, яғни:
(6.2)
Жалпыланған мақсат функция (6.1) жекеленген критериялар-ды орау үшін қолданылуы мүмкін,мынадай жағдайларда, егер:
– маңыздылығы бойынша жекеленген (локальдылар) крите-риялар, бір-бірімен салыстыра алатындай, сандық шама-лармен өлшенетін болса, яғни олардың әрқайсысын бір көрсеткішпен µj және оның сандық мәнімен бағалай алатын болсақ;
– жекеленген критериялар бір тектес болса (бірдей өлшем бірлікпен өлшенсе; біздің мысалда «жабдықтардың баға-лары» және «жабдықтардың өнімділігі» бір тектес).
Мұндай жағдайда көпкритериялы оңтайластыру есептерін шығаруға аддитивтік оңтайластыруды қолдану өте дұрыс шешім болып есептелінеді.
Айталық, мысалда оңтайлы жабдықтар нұсқасын екі локаль-ды критерия бойынша таңдайтын болып шештік делік:
– өнімділігі (а.ө.б.);
– жабдықтардың бағалары (а.ө.б.).
Осыдан кейін басқа критерияларды есепке алмай, қабылдан-ған критериялардың маңыздылығын эксперттер қайтадан бағалай-ды, айталық, олар сәйкесінше: µ1= 0,667, µ2 = 0,333 болсын. Стратегиялық үш нұсқа (жабдықтарды шығаратын 3-зауыт) үшін аддитивтік оңтайластыру критериясын есептейміз:
Көріп отырмыз екі жекеленген критериялар бойынша жаб-дықтардың 1-ші нұсқасы (яғни 1-ші зауытта жасалынған) оңтайлы, Fmax=F1(a1j)=5,666.
Біздің мысалда 4 критерия қарастырылған. Бірақ олар бір тектес емес, яғни өлшем бірліктері әртүрлі. Сондықтан критерия-ларды нормальдау қажет. Барлық критерияларды нақтылы өлшем бірліксіз бір масштабқа, яғни бір өлшемге келтіретін әрекетті нормализациялау деп атайды. Қазіргі кезде нормализациялау әре-кетінің көптеген сүлбесі жасалынған. Солардың кейбіреуін қарас-тырайық.
Әрбір локальдық критериялардың максимумы және миниму-мы анықталынады, яғни:
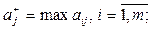(6.3)
(6.4)
Есепті шешкен кезде критериялары максимальданылатын 
және минимальданылатын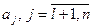 
топтарға бөлеміз.
Онда максимальды нәтижелілік принципіне сәйкес нормаль-данылған критериялар келесідей қатынастар арқылы анықталына-ды:
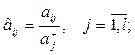(6.5)
(6.6)
немесе 
(6.7)
(6.8)
Мақсат функцияның мәні максимальды болуын қамтамасыз ететін нұсқа (стратегия) оңтайлы делінеді, яғни:
(6.9)
Минимальды нәтижелілік принципіне сәйкес нормальданыл-ған критериялар келесідей қатынастар арқылы анықталынады:
(6.10)
(6.11)
немесе 
(6.12)
(6.13)
Мақсат функцияның (6.9) мәні минимальды болуын қамтама-сыз ететін нұсқа (стратегия) оңтайлы делінеді.
Енді қарастырылып отырған мысалды 4 локальды критерия-лар мен шешіп көрелік. Мысалда, жабықтар үш зауыттарда шыға-рылады (m = 3), стратегиямыз - қандай зауытта жасалған жаб-дықтар оңтайлы, локальды критерияларымыз (n=4).
Шешімі
1. Әрбір локальдық критериялардың (6.3) және (6.4) форму-лалар бойынша max және min анықтайық:
– өндірушілігі – 
(1-зауыт) және 
(2-зауыт);
– жабдықтар бағасы – 
(1-зауыт) және 
(2-зауыт);
– энергосиымдылығы – 
(2-зауыт) және 
(3-зауыт);
– сенімділігі – 
(1-зауыт) және 
(2-зауыт).
2. Есепті шешу барысында бірінші (өндірушілік) және төртінші (сенімділік) критериялары максимальданылады (бұл бірінші топ), екінші (жабдықтар бағасы) және үшінші (энерго-сиымдылық) критериялары минимальданылады (екінші топ).
3. Максимальды нәтижелілік принципі бойынша критерия-ларды нормальдаймыз:
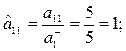
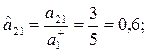
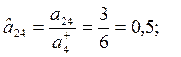
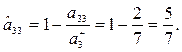
4. Әрбір нұсқа бойынша жалпыланған функцияны анықтай-мыз:
Бірінші нұсқа, яғни 1-зауытта жасалынған жабдықтарды таңдау оңтайлы, себебі Fmax=F1= 0.729.
Сөйтіп, көпкритериялы есептерді шешуде қазіргі кезде бірнеше әдістер мен тәсілдерді кездестіруге болады. Қарастырыл-ған әдіс көбінесе экономикалық есептерді шешуде қолданылады.
Көпкритериялы есептерді шығаруда жиі қолданылатын келесі қызықты әдістің бірі кезектерімен жол беру (уступка) әдісі. Аталған әдіс келесідей тәртіппен жүргізіледі. Бірінші кезекте критериялардың маңыздығы (бұл кезде салмақтар коэффициенті µi ешқандай роль атқармайды) бойынша ретелінініп, нөмірленеді. Ең жоғары маңыздысы бірінші және бірінші нөмірлі, одан кейінгі маңыздысы екінші және екінші нөмірлі және сол ретпен ең аз маңыздысы соңғы нөмірлі болып орналастырылады. Маңыздылы-ғы бойынша бірінші критерия a1 оңтайластырылады, яғни оның экстремальды a1* мәні анықталынады. Осыдан кейін оңтайлы мәннен қанша шамаға дейін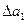 
ауытқу (жол беру) мүмкін бола алатыны тағайындалады. Бірінші критерияның оңтайлы мәнінен ауытқу шамасы жол беру шамасынан асып кетпеген жағдайда маңыздығы екінші орындағы критерияның a2 экстремальды мәні (max немесе min) ізделінеді және осы екінші критерия үшін 
шамасы тағайындалынады. Әрі қарай есептің үшінші критериясы бойынша осы ретпен оңтайластыру жүргізіледі және т.б.с.с. Сонымен, көпкритериялы оңтайластыру есебі кезекпен бір крите-риялы есептердің шешім технологиясына ауыстырылады. Кейінгі есептерді шешуде, жол беру мәндерін ескерген шектеулерден тұратын, қосымша шарттарды қалыптастыру үшін алғашқы есептердің шешім нәтижелері қолданылады.
6.1.2 Тәуекелдік жағдайларда шешімдер қабылдау
Тәуекелдік жағдайларда шешімдер қабылдауда қолданыла-тын негізгі бағалау критериялары:
- нәтиженің күтілетін мәні;
- дисперсиясын минимальдап, үйлестірген нәтиженің күті-летін мәні;
- нәтиженің жететін белгілі деңгейі;
- жоғары ықтималды келешекте болатын жағдай (алғашқы).
Нәтижелік мәндердің (пайда, шығын, экономикалық шығын-дар және т.б.с.с.) экстремальдық мәндерін (max немесе min) анықтау керек болған жағдайда күтілетін мән критериясы қолданылады. Осы критерияларды қолдану тәсілдерін нақтылы мысал қарастыру арқылы талқылайық. Мысалы, бір топ автомо-бильдерге профилактикалық жөндеу жұмыстарын жүргізуге ықпал жасалынбақшы. Техникалық қызмет көрсету (ТҚК) артық жасалған және тоқтап қалу, жұмысқа жарамсыз жағдайлар жоспарланбаған, бірақ олардың тәуекелдіктерін ескеріп, берілген жасалынған жұ-мысқа (жүріп өткен қашықтыққа) Lk кеткен шығын сомасын белгілі бір шекке дейін минимальдау арқылы, профилактикалық жөндеуге жасалатын ықпалдардың оңтайлы саны, берілген жаса-лынған жұмыста (жүріп өткен қашықтықта) жүргізілген ТҚК са-нымен теңестіріледі. Жедел қалпына келтіру көзделген жөндеуге сұраныс ықтималдығының моделі берілген есептің моделі болып есептелінеді. Онда жасалынған жұмысқа (жүріп өткен қашық-тыққа) Lk, атап айтқанда, жоспарлы жөндеуге Sp, профилактикаға SТҚК және жоспарланбаған кездейсоқ жөндеуге Sкж (жұмысқа жа-рамсыз болатын кездердің жоспарланбай жіберіліп қойылуы жө-нінде штраф ретінде қарастырылған) кеткен шығындар сомасы мини-мальданылады:
S = Sp + SТҚК + Sкж→min (6.14)
Шығындар сомасында (6.14) қарастырылған көрсеткіштердің шамалары, мына формуламен анықталатын:
(6.15)
жасалынған жұмыс (жүріп өткен қашықтық) Lk кезінде жүргізілген профилактикалық жөндеу санымен (m) тығыз байланысты. Мұн-дағы Lжж - жарамсыз жағдай пайда болғанға дейінгі жасалған жұмыс (жүріп өткен қашықтық).
Жарамсыз жағдайға жеткенге дейінгі жасалған жұмыс (жүріп өткен қашықтық) Lжж, таратып бөлу тығыздығымен f(Lжж), Lжж<Lk анықталатын, кездейсоқ шама. Мұндағы Lжж кездейсоқ шама бо-луына байланысты n шамасы да кездейсоқ. Оның таратып бөлу тығыздығы:
(6.16)
Функция f(n)-ді салмақ функциясы ретінде қолданып және (6.14) формуласындағы шығындар сомасы мүшелерін, оларға сәй-кес бағалар арқылы өрнектеп, мынаны аламыз:
(6.17)
мұндағы Cp– ескертулі (жоспарлы) жөндеулердің орташа бағасы;
Cжж– профилактикалық жөндеулердің орташа бағасы (немесе
қорды толық пайдаланбай жоспарсыз жүргізілген ТҚК
кезде кейбір детальдар ауыстырылуына байланысты
шығыс);
Cш– жұмысқа жарамсыз жағдайға байланысты шығын
(штраф) (немесе жарамсыз жағдайдан өту үшін
жасалған жұмыстар шығыны). Сөзсіз, Cш > Cжж.
(6.17) формуладағы интегралда [0, np ] ТҚК артық орындау (ТҚК шығын артық жұмсалған) тәуекелдігіне сәйкес, ал инте-гралда [np, ∞] аралық – авариялық жарамсыздануды жіберіп қою тәуекелдігіне (қажеттігіне байланыстты техникалық жөндеуге кет-кен шығын артық қолданған) сәйкес. Жүріп өткен қашықтық Lk (жалпы Lk – капиталдық жөндеуден өткенге дейінгі жүріп өткен қашықтық ) бойынша (6.17) теңдеуінен қанша жөндеу жүргізілген, солардың оңтайлы np санын анықтаймыз. Одан кейін ТҚК жүргізу-ге дейінгі жүріп өтетін қашықтықты анықтаймыз:
. (6.19)
Мысал.Жүріп өткен қашықтық Lk=200 мың км, Cш=69, Cp=24, Cжж=15 болғанда, ТҚК (ш.ө.б.) оңтайлы жүргізу аралықтарын анықтаңыз. Жарамсызданып, тоқтап қалғанға дейінгі жасалған жұмыстың (жүріп өткен қашықтық) тығыздығы нормальдық тара-тып бөлу заңдылығына бағынсын және оның параметрлері: 
=20 мың км және σL= 5 мың км болсын, сонымен қатар нормаль-дық таратып бөлу функциясы:
(6.19)
Шешімі
(6.15) формула бойынша (6.19) таратып бөлу тығыздығының формуласын түрлендіру арқылы (n ≥1) болатынын анықтап, мына өрнекті тұрғыздық: