 |
|
Первісна функції комплексної змінної.
Інтегральна теорема Коші
Якщо крива  лежить в області аналітичності функції
лежить в області аналітичності функції 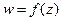 , то комплексний інтеграл
, то комплексний інтеграл  не залежить від форми шляху інтегрування, а тільки від початкової та кінцевої точок. Це пояснюється тим, що для аналітичної функції виконуються умови Коші–Рімана
не залежить від форми шляху інтегрування, а тільки від початкової та кінцевої точок. Це пояснюється тим, що для аналітичної функції виконуються умови Коші–Рімана  і
і 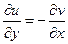 , які співпадають з умовами незалежності від шляху інтегрування обох відповідних дійсних криволінійних інтегралів
, які співпадають з умовами незалежності від шляху інтегрування обох відповідних дійсних криволінійних інтегралів  і
і  .
.
Таким чином, інтеграл аналітичної функції можна подати у вигляді  .
.
Якщо зафіксувати нижню межу інтегрування, то одержаний інтеграл  , як функція верхньої межі, служить первісною для
, як функція верхньої межі, служить первісною для  :
:
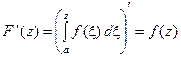 .
.
Множина всіх первісних для даної функції утворює відповідний невизначений інтеграл.
Для інтеграла аналітичної функції справджується формула Ньютона – Лейбніца
 ,
,
де  – довільна первісна.
– довільна первісна.
Зауваження. Таблиця інтегралів аналогічна відповідній таблиці для функцій дійсного аргументу, але підлогарифмові вирази не містять модулю.
Приклад. Користуючись таблицею інтегралів, обчислити заданий інтеграл аналітичної функції:
 .
.
Розв’язання. 

 .
.
Умови незалежності криволінійного інтеграла  від форми шляху інтегрування
від форми шляху інтегрування  еквівалентні рівності нулю цього інтеграла по довільному замкненому контуру
еквівалентні рівності нулю цього інтеграла по довільному замкненому контуру  , що лежить в даній однозв’язній області
, що лежить в даній однозв’язній області
 .
.
Аналогічне твердження справедливе для комплексного інтеграла аналітичної функції.
Теорема (інтегральна теорема Коші для однозв’язної області). Якщо функція  аналітична в однозв’язній області
аналітична в однозв’язній області  , що обмежена кусково-гладким контуром
, що обмежена кусково-гладким контуром  і неперервна в замкненій області
і неперервна в замкненій області  , то інтеграл функції
, то інтеграл функції  по контуру
по контуру  дорівнює нулю
дорівнює нулю
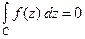 .
.
Теорема Коші поширюється на багатозв’язну область (рис. 23): якщо функція  аналітична в багатозв’язній області
аналітична в багатозв’язній області  , що обмежена зовнішнім контуром
, що обмежена зовнішнім контуром  і внутрішніми контурами
і внутрішніми контурами  , і неперервна в замкненій області
, і неперервна в замкненій області  , то інтеграл функції
, то інтеграл функції  по повній межі області в додатному напрямі дорівнює нулю
по повній межі області в додатному напрямі дорівнює нулю

 .
.
Іншими словами, для складеного контуру справедливо: інтеграл функції  по зовнішньому контуру дорівнює сумі інтегралів по всіх внутрішніх контурах при умові, що обіг усіх контурів здійснюється проти годинникової стрілки
по зовнішньому контуру дорівнює сумі інтегралів по всіх внутрішніх контурах при умові, що обіг усіх контурів здійснюється проти годинникової стрілки
 .
.
При доведенні багатозв’язна область перетворюється в однозв’язну область за допомогою розрізів 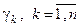 , що з’єднують внутрішні контури із зовнішнім (рис. 23). Кожна лінія розрізу
, що з’єднують внутрішні контури із зовнішнім (рис. 23). Кожна лінія розрізу 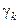 проходиться двічі в протилежних напрямах, тому інтеграли по ній при додаванні взаємно знищуються.
проходиться двічі в протилежних напрямах, тому інтеграли по ній при додаванні взаємно знищуються.
5.3. Інтегральна формула Коші та її наслідки
Інтегральна теорема Коші відкриває можливість визначення значень аналітичної функції всередині області через її значення на межі цієї області.
 Нехай функція
Нехай функція  аналітична в однозв’язній області
аналітична в однозв’язній області  , що обмежена кусково-гладким контуром
, що обмежена кусково-гладким контуром  і неперервна в замкненій області
і неперервна в замкненій області  (рис. 24). Для довільної фіксованої внутрішньої точки
(рис. 24). Для довільної фіксованої внутрішньої точки  області
області  допоміжна функція
допоміжна функція  є аналітичною в цій області, крім хіба що точки
є аналітичною в цій області, крім хіба що точки  . Обведемо точку
. Обведемо точку  колом
колом 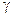 з центром у цій точці та радіусом
з центром у цій точці та радіусом 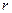 таким, що все коло лежить всередині області
таким, що все коло лежить всередині області  . Тоді допоміжна функція
. Тоді допоміжна функція  буде аналітичною у двозв’язній області
буде аналітичною у двозв’язній області  між контурами
між контурами 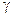 і
і  . За теоремою Коші
. За теоремою Коші
 ;
;  .
.
Тоді



 .
.
Із неперервності підінтегральної функції випливає, що останній інтеграл прямує до нуля при  і при
і при 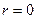 стає рівним нулю. Дістаємо інтегральну формулу Коші (інтеграл Коші)
стає рівним нулю. Дістаємо інтегральну формулу Коші (інтеграл Коші)
 .
.
Зауваження 1. У випадку багатозв’язної області інтегрування треба проводити по повній межі у додатному напрямі.
Зауваження 2. Оскільки  – довільна точка області аналітичності, то індекс можна опустити, а межові точки позначити через
– довільна точка області аналітичності, то індекс можна опустити, а межові точки позначити через 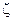 . Тоді формула Коші (інтеграл Коші) набуває вигляду
. Тоді формула Коші (інтеграл Коші) набуває вигляду
 .
.
Інтеграл Коші виражає значення аналітичної функції  в довільній точці
в довільній точці  через її значення
через її значення 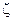 на довільному контурі
на довільному контурі  , що лежить в області аналітичності функції
, що лежить в області аналітичності функції  і містить точку
і містить точку  всередині. В цей інтеграл змінна
всередині. В цей інтеграл змінна  входить як параметр.
входить як параметр.
Наслідок 1. 
Зауваження 3. Нехай функція  – аналітична в області
– аналітична в області  з межею
з межею  і неперервна в замкненій області
і неперервна в замкненій області  . Нехай
. Нехай  – довільна точка межі
– довільна точка межі  . Тоді в силу неперервності функції
. Тоді в силу неперервності функції  до самої межі
до самої межі  з наслідку 1 випливає:
з наслідку 1 випливає:
 ;
;  .
.
Таким чином, на межі області  функція
функція  має стрибок, що дорівнює
має стрибок, що дорівнює  – значенню цієї функції на межі.
– значенню цієї функції на межі.
Наслідок 2. Нехай функція  – аналітична в області
– аналітична в області  з межею
з межею  і
і  – довільна внутрішня точка цієї області. Тоді функція
– довільна внутрішня точка цієї області. Тоді функція  нескінченно разів диференційовна, причому
нескінченно разів диференційовна, причому
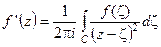 ;
; 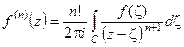 .
.
Ці співвідношення одержуються диференціюванням інтеграла Коші, де похідна по параметру береться від підінтегральної функції.
Теорема і формула Коші знаходять широке застосування при обчисленні інтегралів по замкнутих контурах.
Приклад. Обчислити інтеграл  по вказаному замкненому контуру
по вказаному замкненому контуру  :
:
а) 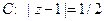 ; б)
; б)  ; в)
; в)  .
.
Розв’язання. Підінтегральна функція  всюди аналітична за винятком двох особливих точок
всюди аналітична за винятком двох особливих точок 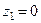 і
і 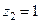 .
.
 а) Особлива точка
а) Особлива точка 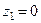 не входить всередину області
не входить всередину області  , обмеженої контуром
, обмеженої контуром 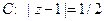 (рис. 25). У підінтегральному виразі виділимо функцію
(рис. 25). У підінтегральному виразі виділимо функцію 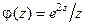 , що аналітична в області
, що аналітична в області  . Тоді для обчислення інтеграла можна скористатися формулою Коші для першої похідної:
. Тоді для обчислення інтеграла можна скористатися формулою Коші для першої похідної:

 .
.
 б) Обидві особливі точки
б) Обидві особливі точки 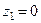 і
і 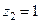 не входять всередину області
не входять всередину області  , обмеженої контуром
, обмеженої контуром  (рис. 26). Підінтегральна функція
(рис. 26). Підінтегральна функція  аналітична в цій області, тоді за теоремою Коші
аналітична в цій області, тоді за теоремою Коші
 .
.
 в) Обидві особливі точки
в) Обидві особливі точки 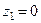 і
і 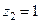 входять всередину області
входять всередину області  , обмеженої контуром
, обмеженої контуром  (рис. 27). Побудуємо кола
(рис. 27). Побудуємо кола  і
і  з центрами відповідно в точках
з центрами відповідно в точках 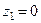 і
і 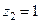 достатньо малих радіусів так, щоб вони не перетинались ні з контуром
достатньо малих радіусів так, щоб вони не перетинались ні з контуром  , ні між собою. У тризв’язній області, обмеженій ззовні контуром
, ні між собою. У тризв’язній області, обмеженій ззовні контуром  , а зсередини – колами
, а зсередини – колами  і
і  , підінтегральна функція
, підінтегральна функція  аналітична. За теоремою Коші для складеного контуру
аналітична. За теоремою Коші для складеного контуру
 ,
,
де обхід всіх контурів здійснюється проти годинникової стрілки.
У підінтегральному виразі першого доданка виділимо функцію 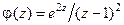 , що аналітична в області, обмеженій контуром
, що аналітична в області, обмеженій контуром  . Тоді за формулою Коші:
. Тоді за формулою Коші:


 .
.
Другий доданок  не залежить від вибору контуру
не залежить від вибору контуру  , що охоплює тільки одну особливу точку
, що охоплює тільки одну особливу точку 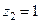 , тому його значення співпадає з обчисленим в пункті а). Отже,
, тому його значення співпадає з обчисленим в пункті а). Отже,
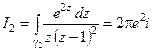 .
.
Таким чином,
 .
.
6. Ряди функцій комплексної змінної