 |
|
Обчислення інтегралів за допомогою лишків
Обчислення комплексних інтегралів по замкненому контуру. За допомогою лишків можна обчислювати інтеграли по замкненому контуру від однозначних функцій, що не містять особливостей на контурі, або від однозначних гілок багатозначних функцій, якщо всередині контуру відсутні точки розгалуження.
Приклад 1. Обчислити комплексний інтеграл
 ,
,
де а)  ; б)
; б)  .
.
Розв’язання.
Підінтегральна функція 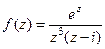 має три особливі точки (самостійно переконайтеся в цьому і дослідіть їх характер):
має три особливі точки (самостійно переконайтеся в цьому і дослідіть їх характер): 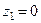 – полюс третього порядку,
– полюс третього порядку,  – простий полюс,
– простий полюс,  – істотно особлива точка ((рис. 32).
– істотно особлива точка ((рис. 32).
 а) Усередині кола
а) Усередині кола  розміщена тільки одна особлива точка
розміщена тільки одна особлива точка 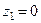 – полюс третього порядку. За основною теоремою про лишки
– полюс третього порядку. За основною теоремою про лишки
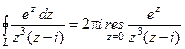 ;
;



 ;
;
 .
.
б) Перший спосіб. Усередині кола  розміщені дві особливі точки
розміщені дві особливі точки 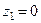 – полюс третього порядку і
– полюс третього порядку і  – простий полюс. За основною теоремою про лишки
– простий полюс. За основною теоремою про лишки
 ;
;
 ;
;
 .
.
Другий спосіб. Зовні кола  розміщена тільки одна особлива точка
розміщена тільки одна особлива точка  – істотно особлива. За наслідком 2 із основної теореми про лишки
– істотно особлива. За наслідком 2 із основної теореми про лишки
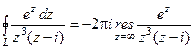 .
.
Розвинемо підінтегральну функцію  в ряд Лорана:
в ряд Лорана:
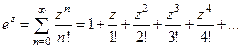 ;
;
 ;
;
 .
.
Звідси


 ;
; 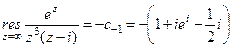 .
.
Тоді
 .
.
Обчислення дійсних інтегралів за допомогою переходу до комплексних інтегралів. Звичайно, контур інтегрування вибирають так, щоб інтеграл по деякій частині контуру при необмеженому його розширенні перетворювався в заданий дійсний інтеграл, а інтеграл по частині, що залишилася, прямував до нуля.
Лема (лема Жордана). Нехай  – додатне число
– додатне число  і
і  – півколо
– півколо  , що лежить в області
, що лежить в області  – верхній півплощині
– верхній півплощині 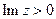 (рис. 33). Якщо функція
(рис. 33). Якщо функція  – аналітична в області
– аналітична в області  за винятком скінченного числа
за винятком скінченного числа 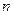 ізольованих особливих точок
ізольованих особливих точок 
 і прямує до нуля в цій області, коли
і прямує до нуля в цій області, коли  , тоді
, тоді
 .
.
 Наслідок. Нехай функція
Наслідок. Нехай функція  дійсної змінної
дійсної змінної  неперервна на всій дійсній осі
неперервна на всій дійсній осі  , а відповідна функція
, а відповідна функція  комплексної змінної
комплексної змінної  задовольняє лемі Жордана, тоді
задовольняє лемі Жордана, тоді
 .
.
Приклад 2. Обчислити дійсний невласний інтеграл
 .
.
Розв’язання. Підінтегральна функція  неперервна на дійсній осі, а відповідна комплексна функція
неперервна на дійсній осі, а відповідна комплексна функція  аналітична у верхній півплощині за винятком однієї особливої точки
аналітична у верхній півплощині за винятком однієї особливої точки  – полюса другого порядку. Крім того,
– полюса другого порядку. Крім того,  при
при  . Знайдемо лишок:
. Знайдемо лишок:

 .
.
Тоді за наслідком леми Жордана (при  )
)
 .
.
Приклад 3. Обчислити дійсний невласний інтеграл
 .
.
Розв’язання. Застосуємо заміну  .
.
Відповідна комплексна функція 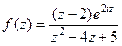 у верхній півплощині має одну особливу точку
у верхній півплощині має одну особливу точку  – простий полюс. Знайдемо лишок:
– простий полюс. Знайдемо лишок:

 .
.
Тоді, виділяючи дійсну частину, за наслідком леми Жордана отримаємо

 .
.
Зауваження. Інколи зручно формувати контур інтегрування у вигляді прямокутника чи криволінійного трикутника.