Главная | Обратная связь

Линейные преобразования линейных пространств

Определение 2. Линейное отображение j: L®L назовем линейным преобразованием L (т.е. линейное преобразование L – это линейное отображение L в себя).

Примеры линейных преобразований:

I. Линейными преобразованиями пространства R₂ являются:

1. Проектирование на некоторую ось;

2. Преобразование растяжения (j(a)=aa "aÎR₂);

3. Поворот плоскости на некоторый угол;

4. Симметрия относительно оси, относительно точки;

II. Дифференцирование пространства многочленов P[x]

(f(x)® f ´(x)).

Для описания линейных преобразований конечномерных линейных пространств удобно использовать матрицы.

Определение 3. Пусть j – линейное преобразование конечномерного линейного пространства L, е=(e₁,…,e_n) – некоторый базис этого пространства. Матрица А, столбцы которой являются координатными столбцами векторов j(е₁),…,j(е_n) в базисе e, называется матрицей линейного преобразования j в базисе е.

Чтобы составить матрицу А линейного преобразованияj в базисе е, нужно найти векторы j(е₁),…,j(е_n) и выразить каждый из них через базис е:

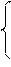j(e₁)=a₁₁е₁+…+a_n1е_n

............................. (5)

j(e_n)= a_1nе₁+…+a_nnе_n.

Тогда

A=

.

Замечание 1.Если ввести обозначение j(е)=(j(е₁),…,j(е_n)), то равенства (5) перепишутся в виде: j(е)=еА. Это - матричная форма определения матрицы линейного преобразования.

Теорема 1. Пусть j – линейное преобразование n-мерного линейного пространства L над Р, е=(e₁,…e_n) – базис L, А – матрица преобразования j в базисе e. Тогда отображение w: j®A – биекция множества F всех линейных преобразований пространства L на множество M_n(P) всех матриц n-го порядка с элементами из поля Р.

Доказательство. Из определения матрицы линейного преобразования видно, что j в базисе е имеет единственную матрицу А. Потому w: j®A – отображение множества F в множество M_n(P). Далее, если АÌM_n(P), то обозначим через c₁,…,c_n векторы из L, координатами которых в базисе е являются столбцы матрицы А. По лемме 2 существует такое линейное преобразование jÎF, что j(e_i)=c_i (i=1,…, n). Тогда А – матрица линейного преобразования j в базисе е, т.е. w: j®A. Значит, w – сюръекция.

Осталось доказать, что w - инъекция. Если j, yÎF и w(j)=w(y)=А, то j(e_i)=y(e_i) (i=1,…,n). По лемме 1 j=y. Этим доказано, что w - биекция.

Теорема доказана.

Следствие. Любая матрица n-го порядка с элементами из поля Р является матрицей некоторого линейного преобразования произвольного n-мерного линейного пространства над Р (это утверждение доказано в ходе доказательства теоремы 1).

Замечание 2. Теорема 1 означает, что изучение линейных преобразований конечномерных линейных пространств и квадратных матриц над Р – это близкие задачи.