Главная | Обратная связь

Программа дисциплин

Тема 1. Элементы векторной и линейной алгебры

Определители второго и третьего порядков, их свойства, вычисление. Решение систем линейных уравнений методом Крамера. Матрицы, действия над ними, обратная матрица, решение систем линейных уравнений матричным способом. Векторы. Скалярное, векторное, смешанное произведения векторов, их свойства, приложения.

 

Определители. Системы

Выражение вида 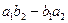называется определителем второго порядка и обозначается

.

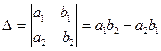Рассмотрим систему:

,

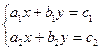где

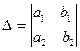- главный определитель;

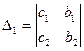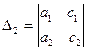, - вспомогательные определители. Они получаются заменой в главном определителе колонки коэффициентов при х (D₁) и при y (D₂) колонкой свободных членов.

Решение системы по правилу Крамера имеет вид:

.

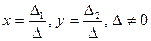Определителем третьего порядка называется число, обозначаемое символом

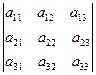
и вычисляемое по правилу Саррюса:

.

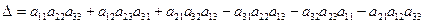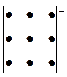
Произведения этих элементов Произведения этих элементов

берем со своими знаками берем с противоположными

знаками

 

Для систем трех уравнений с тремя неизвестными

правило Крамера имеет вид:

,

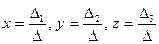где

Пример

 

Найти решение системы с помощью правила Крамера.

 

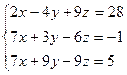
Решение

.

 

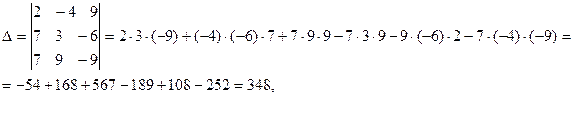
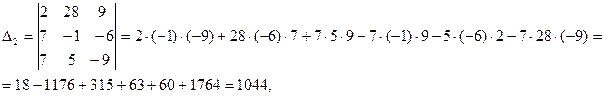
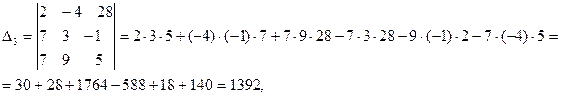
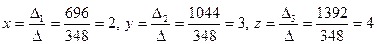Ответ: (2, 3, 4).

ВЕКТОРНАЯ АЛГЕБРА

 

Векторы

 

Вектором называется направленный отрезок прямой или упорядоченная пара точек (про которые известно, какая первая – начало, какая вторая – конец).

Обозначают: или .

Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными: .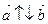

Если , то

1) 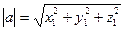- длина вектора;

2) ;

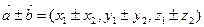3) 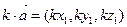, k- число;

4) .

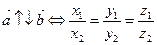Если заданы две точки A(x₁, y₁, z₁) , B(x₂, y₂, z₂), то

1)

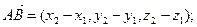
2) если 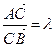, тогда координаты точки С, делящей отрезок в заданном отношении, находится по формулам:

.

 

 

В частности, если С – середина отрезка, то

.
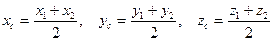