Главная | Обратная связь

Плоскость в пространстве

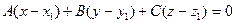-уравнение плоскости, проходящей через точку , перпендикулярно вектору - нормали к плоскости.

 

-уравнение плоскости, проходящей через три заданные точки .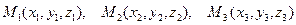

 

 

Если две плоскости заданы общими уравнениями:

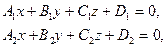
то по уравнениям двух плоскостей можно определить их нормали .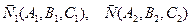

На основании теоремы об углах, образованных взаимно перпендикулярными сторонами, один из углов между плоскостями можно определить как угол между нормалями по формуле:

.

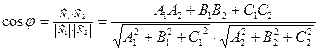Пример

 

Составить уравнение плоскости А₁А₂А₃, если А₁(2, 0, ,3), А₂(-1, 0, 8), А₃(0,2,4).

Воспользуемся уравнением плоскости, проходящей через три точки:

,

,

 

.

Раскроем определитель:

 

(x-2)∙0+y∙5∙(-2)+(z-3)∙(-3)∙2-(z-3)∙0-(x-2)∙2∙5-y∙(-3)∙1=0;

-10(x-2)-7y-6(z-3)=0;

-10x-7y-6z+38=0 –

уравнение плоскости А₁А₂А₃.

 

Литература [ 3]

Вопросы для самопроверки:

1. Что называется направляющим вектором прямой?

2. Что называется угловым коэффициентом прямой на плоскости?

3. Как записывается уравнение прямой, проходящей через две точки?

4. Как записывается уравнение плоскости, проходящей через три точки?

Тема 3. Введение в анализ

Понятие функции. Предел функции, основные теоремы о пределах. Бесконечно малые и бесконечно большие функции, связь между ними. Непрерывность функции. Свойства функций, непрерывных на отрезке.

 

Пределы

1. Функция называется бесконечно малой при х→а , если .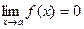

2. Функция называется бесконечно большой при х→а, если она по модулю больше любого наперед заданного положительного числа.

Символическая запись:

.

3. Если f(x) – бесконечно большая функция при х→а, то - бесконечно малая функция при х→а.

4. Если f(x)≠0 – бесконечно малая функция при х→а, то - бесконечно большая функция при х→а.

 

Примеры

1) ;

2) ;

3) .

Неопределенность

Чтобы раскрыть неопределенность такого вида, надо числитель и знаменатель почленно разделить на неизвестное слагаемое в наивысшей степени.

 

Пример

.

 

Для контроля следует помнить:

1) если степени многочленов в числителе и знаменателе равны, то предел равен отношению старших коэффициентов (коэффициент при высших степенях);

2) если степень числителя выше степени знаменателя, то предел равен

бесконечности;

3) если степень числителя ниже степени знаменателя, то предел равен

нулю.

Неопределенность

1) ,

где P(x), Q(x) – многочлены.

В этом случае надо числитель и знаменатель разделить на (х-а) один или несколько раз.

 

Пример

,

 

тогда 2x²-11x+5=2(x-x₁)(x-x₂)=2(x-5)(x-1/2).

 

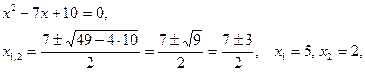
тогда x²-7x+10=(x-5)(x-2);

2) если и есть иррациональность, то числитель и знаменатель надо домножить на сопряженную величину.

Пример

3) первый замечательный предел:

позволяет раскрывать неопределенность .

 

 

Следствия:

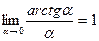
Примеры

1. .

2. .

 

 

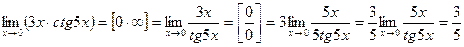Неопределенность 1^∞

Неопределенность такого вида раскрывается с помощью второго замечательного предела:

.

Пример