 |
|
Непрерывность функции в точке
Функция y=f(x) называется непрерывной в точке х=х0, если выполнены условия:
1) функция определена в точке х=х0 и в некоторой окрестности, содержащей эту точку;
2) функция имеет предел в этой точке, т.е.
(существуют и равны между собой односторонние пределы);
3) предел функции равен значению функции в этой точке:
.
Если нарушается хотя бы одно из этих условий, тогда х0 – точка разрыва функции.
Если оба односторонних предела существуют и являются конечными числами, но не выполнено третье условие, то х0 – точка разрыва первого рода. Все остальные точки разрыва – второго рода.
Литература [1, 2]
Вопросы для самопроверки:
1. Как связано понятие предела функции с односторонними пределами?
2. Какая функция называется бесконечно малой, каковы ее свойства?
3. Какая функция называется бесконечно большой, каковы ее свойства?
4. Какая функция называется непрерывной в точке?
Тема 4. Дифференциальное исчисление
Производная функции, ее геометрический, механический и химический смысл. Основные правила и формулы дифференцирования. Производная сложной, обратной функции. Производные высших порядков. Теоремы о среднем. Правило Лопиталя. Условия монотонности функций. Необходимое и достаточное условия экстремума. Выпуклость и вогнутость, точки перегиба графика функции. Асимптоты. Общая схема исследования функции.
Производная
Производной функцией y=f(x) точки х0 называется предел отношения приращения функции Δy в этой точке к вызвавшему его приращению аргумента Δх при произвольном стремлении Δх к нулю, т.е.:
.
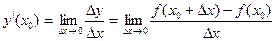Выясним геометрический смысл производной
Напомним, что касательная - есть прямая, занимающая предельное положение секущей.
|
|
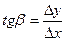, где 
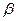-- угол наклона касательной к оси ОХ.
|
|
|
|
При Δх →0, точка М→М0, секущая приближается к своему предельному положению – к касательной, то есть
|
|
.
Рис. 1.
Тогда 
, т.е. производная в точке х0 численно равна тангенсу угла наклона касательной к графику кривой y=f(x) в точке с абсциссой х0.
Тогда , т.е. производная в точке х0 численно равна тангенсу угла наклона касательной к графику кривой y=f(x) в точке с абсциссой х0.
Для сложной функции справедливы формулы:
| 
|
Примеры
1) 
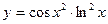
2) 
,
,
3) 
,
.