Замена переменной в определенном интеграле

⇐ ПредыдущаяСтр 9 из 9

Теорема. Пусть f(x) непрерывна на [a, b], введем подстановку 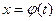. Если

1) 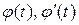непрерывны при ,

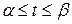2) при изменении t от 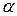до 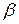функция 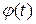изменяется от a до b, 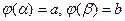, то справедлива формула замены переменной:

Пример:

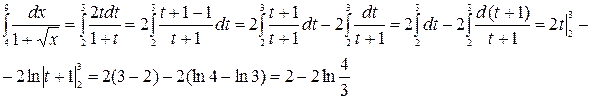
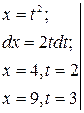
Вычисление площадей плоских фигур

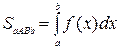– площадь криволинейной трапеции (рис.9).

Рис.9.

Площадь фигуры, ограниченной линиями 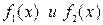(рис.10), находим по формуле .

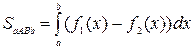Эта формула остается справедливой при любом расположении рассматриваемой фигуры.

Рис.10.

Пример :

Вычислить площадь фигуры, ограниченной линиями: , .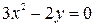

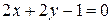1. Найдем точки пересечения данных кривых:

;

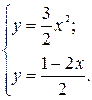
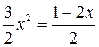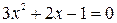Рис.11.

;

; .

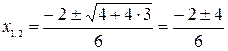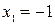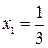2. Построим графики данных функций (рис.11).

(для прямой );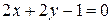

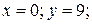
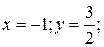
(парабола ).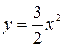

Литература [1, 2]

Вопросы для самопроверки:

1. Что называется определенным интегралом, каков его геометрический смысл?

2. Как выглядит формула Ньютона-Лейбница?

3. Как выглядит формула интегрирования по частям в определенном интеграле?

4. Какие приложения определенного интеграла вы помните?

Тема 7. Несобственные интегралы

Несобственные интегралы с бесконечными пределами и от разрывных функций.

Если в определенном интеграле пределы интегрирования равны ± 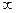или f(x) неопределенна на [a; в] , то возможны случаи:

1. ;

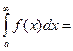
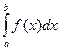2. ;

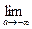
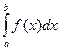3. ;

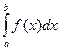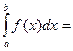
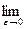
4. 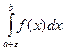; а – точка разрыва

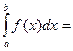
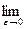
5. 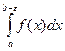; b – точка разрыва.

Если указанные пределы существуют и конечны, то интеграл сходится - если не существуют или бесконечны, то интеграл расходится.

Пример:

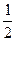
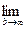
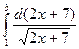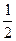
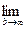= - = 2 = ( - )= .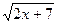

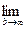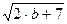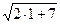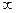Интеграл расходится.

Литература [1, 2]

Вопросы для самопроверки:

1. Дайте определение несобственного интеграла, у которого один предел интегрирования бесконечен.

2. Дайте определение несобственного интеграла, у которого оба предела интегрирования бесконечны.

3. Дайте определение несобственного интеграла, у которого подынтегральная функция терпит разрыв в одном из пределов интегрирования.

Контрольная работа

Перед выполнением контрольной работы студентам необходимо тщательно изучить предложенные темы и разобрать решения приведенных типовых примеров.

Вариант 1

1.Решить систему линейных уравнений по формулам Крамера

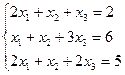2. Даны вершины треугольника. Найти:

а) длину стороны ВС ;

б) уравнение стороны ВС;

в) уравнение высоты, проведенной из вершины А.

А (-3; 1) , В (3;3) , С (3; -2).

3. По координатам вершины пирамиды А₁ А₂ А₃ А₄ , найти:

1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂ и А₁ А₃;

3) площадь грани А₁ А₂А₃;

4) объем пирамиды;

5) уравнение прямой А₁ А₂;

6) уравнение плоскости А₁ А₂А₃.

А₁(2;3;-1) ; А₂(2;-2;4) ; А₃(-1;1;3) ; А₄(1;1;2) .

4.Вычислить пределы функций, не пользуясь средствами дифференциального исчисления:

а) ;

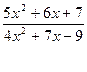б) ;

в) .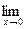

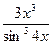5. Найти производные данных функций:

а) y = ;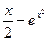

б) y = ;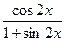

в) у = х .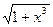

6. Найти точки экстремума и интервалы монотонности функции

у = .

7. Найти неопределенный интеграл:

а) 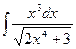; б) .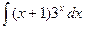

8. Найти определенный интеграл:

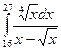9.Вычислить несобственный интеграл или доказать его расходимость

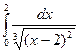10. Найти площади фигур, ограниченных линиями.

у = х – 2х + 2; у=х

Вариант 2

1.Решить систему линейных уравнений по формулам Крамера

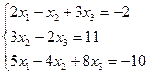2. Даны вершины треугольника.. Найти:

а) длину стороны ВС ;

б) уравнение стороны ВС;

в) уравнение высоты, проведенной из вершины А.

А (-3;2), В (3;4) , С (3;-3).

3. По координатам вершины пирамиды А₁ А₂ А₃ А₄ , найти:

1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂ и А₁ А₃;

3) площадь грани А₁ А₂А₃;

4) объем пирамиды;

5) уравнение прямой А₁ А₂;

6) уравнение плоскости А₁ А₂А₃.

А₁(2;1;-2) ; А₂(4;3;1) ; А₃(6;3;7) ; А₄(-5;-4;8) .

4.Вычислить пределы функций, не пользуясь средствами дифференциального исчисления:

а) ;

б) ;

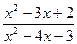в) .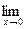

5. Найти производные данных функций:

а) y =2х+ arctg3x;

б) y = (3x-4) tgx;

в) у = .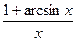

6.Найти точки экстремума и интервалы монотонности функции

у = .

7. Найти неопределенный интеграл:

а) 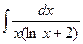; б) .

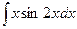8. Найти определенный интеграл:

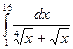9. Вычислить несобственный интеграл или доказать его расходимость

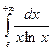10. Найти площади фигур, ограниченных линиями:

у = - х + 4х – 1; у = -х-1.

Вариант 3

1.Решить систему линейных уравнений по формулам Крамера

2. Даны вершины треугольника. Найти:

а) длину стороны ВС ;

б) уравнение стороны ВС;

в) уравнение высоты, проведенной из вершины А.

А (-3;3), В (3;2), С (3;-4).

3. По координатам вершины пирамиды А₁ А₂ А₃ А₄ , найти:

1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂ и А₁ А₃;

3) площадь грани А₁ А₂А₃;

4) объем пирамиды;

5) уравнение прямой А₁ А₂;

6) уравнение плоскости А₁ А₂А₃.

А₁(2;3;5) ; А₂(6;2;3) ; А₃(3;7;2) ; А₄(0;0;1)

4.Вычислить пределы функций, не пользуясь средствами дифференциального исчисления:

а) ;

б) ;

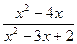в) .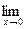

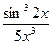5. Найти производные данных функций:

а) y =х + 2lnx;

б) y = (x +1)cos5x ;

в) у = .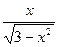

6. Найти точки экстремума и интервалы монотонности функции

у = .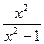

7. Найти неопределенный интеграл:

а) ; б) .

8Найти определенный интеграл:

9. Вычислить несобственный интеграл или доказать его расходимость

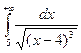10. Найти площади фигур, ограниченных линиями:.

у = х - 4х+ 1; у = х+1.

Вариант 4

1. Решить систему линейных уравнений по формулам Крамера

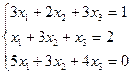2. Даны вершины треугольника. Найти:

а) длину стороны ВС ;

б) уравнение стороны ВС;

в) уравнение высоты, проведенной из вершины А.

А (-3;4), В (3;1), С (3;-5).

3. По координатам вершины пирамиды А₁ А₂ А₃ А₄ , найти:

1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂ и А₁ А₃;

3) площадь грани А₁ А₂А₃;

4) объем пирамиды;

5) уравнение прямой А₁ А₂;

6) уравнение плоскости А₁ А₂А₃.

А₁(2;2;2) ; А₂(4;3;3) ; А₃(4;5;4) ; А₄(5;5;6) .

4. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления:

а) ;

б) ;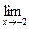

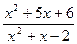в) .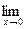

5. Найти производные данных функций:

а) y = ctg + ;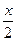

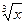б) y = x arcsinx;

в) у = .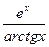

6.Найти точки экстремума и интервалы монотонности функции

у = .

7. Найти неопределенный интеграл:

а) 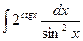; б) .

8. Найти определенный интеграл:

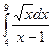9. Вычислить несобственный интеграл или доказать его расходимость

10. Найти площади фигур, ограниченных линиям:.

у = х + 4х; у = х+4 .

Вариант 5

1.Решить систему линейных уравнений по формулам Крамера

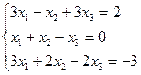2. Даны вершины треугольника. Найти

а) длину стороны ВС ;

б) уравнение стороны ВС;

в) уравнение высоты, проведенной из вершины А.

А (-3;5), В (3;4), С (3;-1).

3. По координатам вершины пирамиды А₁ А₂ А₃ А₄ , найти:

1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂ и А₁ А₃;

3) площадь грани А₁ А₂А₃;

4) объем пирамиды;

5) уравнение прямой А₁ А₂;

6) уравнение плоскости А₁ А₂А₃.

А₁(3;1;4) ; А₂(-1;6;1) ; А₃(-1;1;6) ; А₄(0;4;-1).

4.Вычислить пределы функций, не пользуясь средствами дифференциального исчисления:

а) ;

б) ;

в) .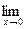

5. Найти производные данных функций:

а) y = sin4х+ 2cos4x ;

б) y = x ∙3 ;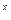

в) у = .

6. Найти точки экстремума и интервалы монотонности функции

у = .

7. Найти неопределенный интеграл:

а) 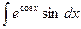; б) .

8. Найти определенный интеграл:

9. Вычислить несобственный интеграл или доказать его расходимость

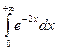10. Найти площади фигур, ограниченных линиями:.

у = - х + 2х; у = -х .

Вариант 6

1.Решить систему линейных уравнений по формулам Крамера

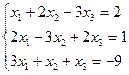2. Даны вершины треугольника. Найти:

а) длину стороны ВС ;

б) уравнение стороны ВС;

в) уравнение высоты, проведенной из вершины А.

А (-2;1), В (4;3), С (4;-2).

3. По координатам вершины пирамиды А₁ А₂ А₃ А₄ , найти:

1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂ и А₁ А₃;

3) площадь грани А₁ А₂А₃;

4) объем пирамиды;

5) уравнение прямой А₁ А₂;

6) уравнение плоскости А₁ А₂А₃.

А₁(3;3;9) ; А₂(6;9;1) ; А₃(1;7;3) ; А₄(8;5;8).

4. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления:

а) ;

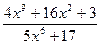б) ;

в) .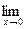

5.Найти производные данных функций:

a) y = tg2x + 3ctgx;

б) y = ;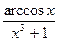

в) у = ( )( ) .

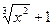6.Найти точки экстремума и интервалы монотонности функции

у = .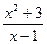

7.Найти неопределенный интеграл:

а) ; б) .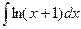

8. Найти определенный интеграл:

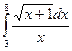9 Вычислить несобственный интеграл или доказать его расходимость

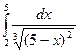10.Найти площади фигур, ограниченных линиями:

у = х + 2х -4; у = х+2.

Вариант 7

1. Решить систему линейных уравнений по формулам Крамера

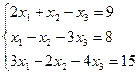2. Даны вершины треугольника. Найти:

а) длину стороны ВС ;

б) уравнение стороны ВС;

в) уравнение высоты, проведенной из вершины А.

А (-2;2), В (4;4), С (4;-3).

3. По координатам вершины пирамиды А₁ А₂ А₃ А₄ , найти:

1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂ и А₁ А₃;

3) площадь грани А₁ А₂А₃;

4) объем пирамиды;

5) уравнение прямой А₁ А₂;

6) уравнение плоскости А₁ А₂А₃.

А₁(3;5;4) ; А₂(5;8;3) ; А₃(1;9;9) ; А₄(6;4;8).

4. Вычислить пределы функций, не пользуясь средствами дифференциального исчисления:

а) ;

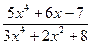б) ;

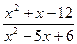в) .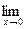

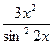5. Найти производные данных функций:

a) y = e + 5lnx;

б) y = (2-x )cos3x;

в) у = .

6.Найти точки экстремума и интервалы монотонности функции

у = .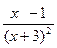

7.Найти неопределенный интеграл:

а) 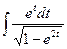; б) .

8.Найти определенный интеграл:

9.Вычислить несобственный интеграл или доказать его расходимость

10. Найти площади фигур, ограниченных линиями.

у = 4 – 6х - х ; у = -х-2.

Вариант 8

1. Решить систему линейных уравнений по формулам Крамера

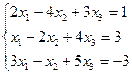2. Даны вершины треугольника. Найти:

а) длину стороны ВС ;

б) уравнение стороны ВС;

в) уравнение высоты, проведенной из вершины А.

А (-2;3), В (4;2), С (4;-4).

3.По координатам вершины пирамиды А₁ А₂ А₃ А₄ , найти:

1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂ и А₁ А₃;

3) площадь грани А₁ А₂А₃;

4) объем пирамиды;

5) уравнение прямой А₁ А₂;

6) уравнение плоскости А₁ А₂А₃.

А₁(2;4;3) ; А₂(3;6;7) ; А₃(7;6;3) ; А₄(4;9;3).

4.Вычислить пределы функций, не пользуясь средствами дифференциального исчисления:

а) ;

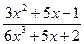б) ;

в) .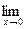

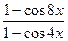5. Найти производные данных функций:

a) y = - ctg2x;

б) y = 3tgx(e 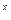-1);

в) у = .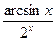

6.Найти точки экстремума и интервалы монотонности функции

у = .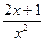

7.Найти неопределенный интеграл:

а) 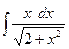; б) .

8. Найти определенный интеграл:

9.Вычислить несобственный интеграл или доказать его расходимость

10.Найти площади фигур, ограниченных линиями:.

у = х - 4х + 3; у = х-3.

Вариант 9

1. Решить систему линейных уравнений по формулам Крамера

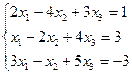2. Даны вершины треугольника. Найти:

а) длину стороны ВС ;

б) уравнение стороны ВС;

в) уравнение высоты, проведенной из вершины А.

А (-2;4), В (4;1), С (4;-5).

3.По координатам вершины пирамиды А₁ А₂ А₃ А₄ , найти:

1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂ и А₁ А₃;

3) площадь грани А₁ А₂А₃;

4) объем пирамиды;

5) уравнение прямой А₁ А₂;

6) уравнение плоскости А₁ А₂А₃.

А₁(4;6;6) ; А₂(4;2;0) ; А₃(6;1;1) ; А₄(1;2;6).

4.Вычислить пределы функций, не пользуясь средствами дифференциального исчисления:

а) ;

б) ;

в) .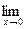

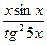5.Найти производные данных функций:

a) y = arctg2x+ ;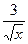

б) y = ;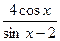

в) у = (tgx-1)arcsinx.

6. Найти точки экстремума и интервалы монотонности функции

у = .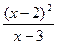

7.Найти неопределенный интеграл:

а) ; б) .

8.Найти определенный интеграл:

9.Вычислить несобственный интеграл или доказать его расходимость

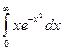10.Найти площади фигур, ограниченных линиями:

у = х - 3х + 2; у = х-1

Вариант 10

1.Решить систему линейных уравнений по формулам Крамера

2 Даны вершины треугольника. Найти:

а) длину стороны ВС ;

б) уравнение стороны ВС;

в) уравнение высоты, проведенной из вершины А.

А (-2;5), В (4;4), С (4;-6).

3.По координатам вершины пирамиды А₁ А₂ А₃ А₄ , найти:

1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂ и А₁ А₃;

3) площадь грани А₁ А₂А₃;

4) объем пирамиды;

5) уравнение прямой А₁ А₂;

6) уравнение плоскости А₁ А₂А₃.

А₁(7;5;3) ; А₂(7;9;6) ; А₃(4;5;7) ; А₄(9;4;4).

4.Вычислить пределы функций, не пользуясь средствами дифференциального исчисления:

а) ;

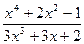б) ;

в) .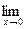

5.Найти производные данных функций:

a) y = 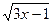+ 2lnx;

б) y = tgx∙sin3x;

в) у = .

6.Найти точки экстремума и интервалы монотонности функции

у = .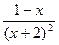

7.Найти неопределенный интеграл:

а) ; б) .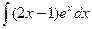

8.Найти определенный интеграл:

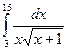9.Вычислить несобственный интеграл или доказать его расходимость

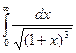10.Найти площади фигур, ограниченных линиями:

у = - х + 6х + 2; у= х+2.

Содержание и оформление контрольной работы

Контрольную работу следует выполнять в отдельной тетради. Следует указать свой шифр и номер варианта. Условие задачи должно быть полностью переписано перед ее решением.

Отмеченные рецензентом ошибки необходимо исправить в конце работы, сделав работу над ошибками.

Зачтенные контрольные работы предъявляются студентом при сдаче зачета или экзамена.

Вопросы для подготовки к экзамену (зачету).

Линейная алгебра

1. Определители второго, третьего порядка, их свойства.

2. Правило Крамера.

Векторная алгебра

1.Действия над векторами. Коллинеарность векторов.

2.Координаты вектора, координаты точки. Действия над векторами в координатной форме. Основные задачи.

3.Скалярное произведение (определение, свойства, координатная форма).

4.Векторное произведение (определение, свойства, координатная форма).

5.Смешанное произведение. Приложения скалярного, векторного и смешанного произведений.

Аналитическая геометрия

1. Уравнение прямой на плоскости.

2. Уравнение прямой в пространстве.

3. Уравнение плоскости в пространстве.

4. Плоскость и прямая в пространстве, их взаимное расположение.

Пределы

1. Способы задания функции. Виды функций.

2. Последовательность. Предел последовательности.

3. Предел функции, односторонние пределы.

4. Теоремы о единственности предела, об ограниченности функции, имеющей предел.

5. Бесконечно малые и бесконечно большие функции.

6. Замечательные пределы.

7. Непрерывность функций в точке. Точки разрыва.

8. Непрерывность функции на отрезке.

Дифференциальное исчисление

1. Определение производной.

2. Геометрический смысл производной.

3. Основные правила дифференцирования.

4. Производная сложной, обратной функций.

5. Теоремы Ферма. Теорема Ролля. Теорема Лагранжа. Теорема Коши. Их геометрический смысл.

6. Возрастание и убывание функции (необходимое и достаточное условия).

7. Экстремумы (необходимое и достаточное условия).

8. Точки перегиба (необходимое и достаточные условия).

9. Выпуклость и вогнутость. Точки перегиба.

10. Правило Лопиталя.

Неопределенный интеграл.

1.Неопределенный интеграл и первообразная. Геометрический смысл неопределенного интеграла.

2.Основные свойства неопределенного интеграла.

3.Методы интегрирования.

Определенный интеграл.

1. Задача, приводящая к понятию определенного интеграла.

2. Определение определенного интеграла.

3.Свойства определенного интеграла.

4.Теоремы об оценке определенного интеграла. Теорема о среднем для определенного интеграла.

5.Формула Ньютона-Лейбница.

6.Методы вычисления определенного интеграла.

7.Вычисление площади фигуры, ограниченной линиями, заданными уравнениями в декартовых координатах.

8.Несобственные интегралы.

Список рекомендуемой литературы

Основная литература

Карасёв А.И. и др. Курс высшей математики для экономистов ч. 1 и 2. М., 2005.
Пискунов Н.С. Дифференциальное и интегральное исчисление. - М.: Наука, 2005. т. 1 и 2.
Высшая математика для экономистов. Под редакцией проф. Н.Ш. Кремера. М., 2005.
Клетеник А.В. Сборник задач по аналитической геометрии. - М.: Наука. 2005.
Берман Г.Н. Сборник задач по курсу математического анализа. - М.: Наука, 2005.
Гмурман В.Е. Сборник задач по теории вероятностей и математической статистике. - М.: Наука, 2005.
Сборник задач по высшей математике для экономистов. Под ред. В.И. Ермакова. М., 2009.

Дополнительная литература

Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. 1,2 том, Изд-во «Высшая школа», 2005 г.
Ильин В.А., Поздняк Э.Г. Аналитическая геометрия. - М.: Наука, 2005.
Ефимов А.В. Краткий курс аналитической геометрии. - М.: Наука, 2005.
Бугров Я.С., Никольский С.М. Задачник. - М.: Наука, 2005.
Кузнецов Л.А. Сборник заданий по высшей математике. - М.: Высшая школа, 2005 г.

МАТЕМАТИКА

Часть 1

Составители: Горшкова Светлана Николаевна

Данович Лариса Михайловна

Арутюнян Ашот Страевич

Наумова Наталья Александровна

Редактор Л.В.Троицкая

Компьютерная верстка Н.Н.Дышкант

________________________________________________________________

Подписано в печать Формат 60´84_1/16.

Бумага оберточная №1. Офсетная печать.

Печ.л. л. 3,5 Тираж 80 экз. Усл.печ.л. 3,2 Изд.№ 165

Уч.-изд.л. 2,4 Заказ №

Цена руб.

Лицензия на издательскую деятельность: ИД № 02586 от 18.08.2000 года.

Издательство КубГТУ: 350072, Краснодар, ул.Московская, 2, кор.А

Лицензия на полиграфическую деятельность: ПД № 10-47020 от 11.09.2002г.

Типография КубГТУ:350058, Краснодар, ул.Старокубанская, 88/4.

⇐ Предыдущая 1 2 3 4 5 6 7 89