Главная | Обратная связь

Прямая на плоскости

- каноническое уравнение

прямой, проходящей через заданную

точку A₁(x₁, y₁) ,параллельно вектору

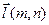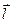, - направляющий вектор.

 

- уравнение прямой,

проходящей через 2 заданные точки

A₁(x₁, y₁), A₂(x₂, y₂).

 

y-y₁=k(x-x₁) - уравнение пучка прямых с

центром A₁(x₁,y₁) и угловым

коэффициентом k.

 

y=kx+b - уравнение прямой с угловым

коэффициентом.

A(x-x₁)+B(y-y₁)=0 - уравнение прямой,

проходящей через точку

перпендикулярно вектору .

- нормаль прямой.

После упрощения последнего уравнения получаем:

Ax+By+C=0 - общее уравнение прямой, где C=-(Ax₁+By₁).

Угловой коэффициент прямой находим по формуле .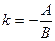

Угол между двумя прямыми равен углу между их нормалями или направляющими векторами (см. скалярное произведение).

Если - угловые коэффициенты двух прямых, то

при - прямые параллельны,

при - прямые перпендикулярны, и обратно.

Пример

 

Составить уравнение прямой, проходящей через точку М(3, 4):

а) параллельно прямой 2x-5y+1=0,

b) перпендикулярно прямой 2x-5y+1=0.

 

Решение

а) 2x-5y+1=0; .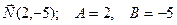

.

Если прямые параллельны, то .

Используем уравнение y-y₁=k(x-x₁), где , М(3, 4).

y-4= (x-3);

5(y-4)=2(х-3);

2x-5y+14=0.

б) если прямые перпендикулярны, то .

;

;

.

 

Прямая в пространстве

-

канонические уравнения прямой в пространстве, проходящей через точку A₁(x₁, y₁, z₁) , параллельно вектору 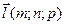, 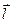- направляющий вектор.

 

Замечание. Если обращается в ноль одна из координат направляющего вектора, например m , то уравнения прямой принимают вид:

(это прямая, лежащая в плоскости x=x₁).

Если равны нулю две координаты направляющего вектора, например m=n=0, то уравнения прямой примут вид:

- эта прямая есть пересечение двух плоскостей x=x₁ и y=y₁, т.е. параллельна оси OZ.

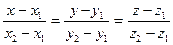- уравнения прямой, проходящей через две точки .

Пример

Составим уравнения прямой А₁, А₂.

А₁(2, 0, 3), А₂(-1, 0, 8), А₃(0, 2, 4).

Воспользуемся уравнениями прямой, проходящей через две точки в пространстве:

;

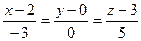- уравнения прямой A₁A₂.

Эта прямая лежит в плоскости (т.е. в плоскости OXZ) и ее уравнения можно записать так:

.