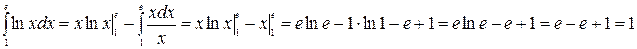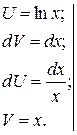 |
|
Понятие определенного интеграла
К нахождению предела, рассмотренного в предыдущем пункте, приводит
ряд задач естествознания. Поэтому рассмотрим предел, отвлекаясь от конкретного смысла задачи.
Пусть на [a, b] задана произвольная функция y=f(x). Применяя для нее схему предыдущей задачи, составим сумму произведений вида
.
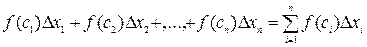Такая сумма называется интегральной суммой функции f(x) на [a, b]. Она
зависит от способа деления [a, b] на элементарные части и от выбора точек
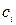на каждой из этих частей.
Определение. Если существует конечный предел последовательности интегральных сумм при 
, не зависящий от способа деления [a, b] и выбора точек 
, то этот предел (число) называется определенным интегралом от функции f(x) на [a, b] и обозначается
_____________________________
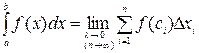
Возвращаясь к задаче о площади криволинейной трапеции, получаем
,
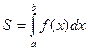т.е. при 
определенный интеграл численно равен площади криволинейной трапеции. В этом состоит геометрический смысл определенного интеграла.
Теорема. Для любой непрерывной на [a,b] функции существует определенный интеграл.
Свойства определенного интеграла
1) 
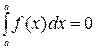; 2) 
;
3) 
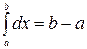; 4)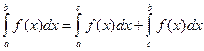 
;
5) 
;
6) Если , то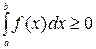 
;
Если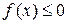 
, то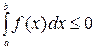 
.
Следствие. Если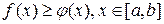 
, то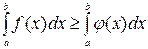 
;
7) если f(x) непрерывна на [a, b], m, M- ее соответственно наименьшее и наибольшее значения на [a, b], то справедлива оценка
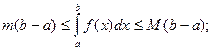
8) (теорема о среднем) . Если f(x) непрерывна на [a, b], то существует хотя бы одна точка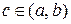 
такая, что
Формула Ньютона-Лейбница
Пусть f(x) – непрерывна на [a, b], F(x) – первообразная функции f(x) на [a,b], тогда определенный интеграл равен приращению первообразной (т.е. неопределенного интеграла) на этом отрезке:
.
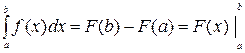Примеры
1) 
;
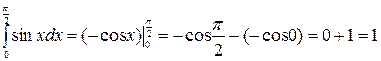2) 
.
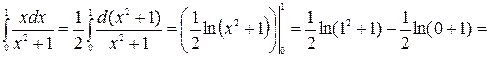
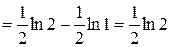Интегрирование по частям
(см. интегрирование по частям в разделе "Неопределенный интеграл")
Формула интегрирования по частям для определенного интеграла имеет вид
Пример.
