Главная | Обратная связь

Исследование функции и построение графика

Исследование проведем по следующему плану:

1. Область определения функции (О.Д.З.)

2. Точки пересечения графика функции с осями координат:

х=0, y=?

y=0, x=?

3. Исследуем функцию на четность или нечетность.

Если область определения функции симметрична относительно х=0 и f(-x)=f(x), то функция четная и ее график симметричен относительно оси OY.

Если область определения функции симметрична относительно х=0 и f(-x)=-f(x), то функция нечетная и ее график симметричен относительно начала координат.

Если не выполнены условия четности и нечетности, то функция общего вида, ее дальнейшее исследование проводим на всей О.Д.З.

4. Исследуем функцию на непрерывность, ищем точки разрыва, если они есть.

5. Асимптоты.

Асимптотой называется прямая, расстояние от которой до переменной точки графика стремится к нулю при удалении этой точки по графику от начала координат.

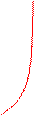
1) если х₀ - есть точка разрыва функции II рода, то прямая х=х₀ есть вертикальная асимптота графика функции (рис.2);

2) наклонные асимптоты графика имеют вид y=kx+b, где

и эти пределы конечны (рис.3).

Если хотя бы один предел не существует или равен бесконечности, то график функции не имеет наклонных асимптот.

Если k=0, b – конечное число, то y=b - есть горизонтальная асимптота (рис.4).

 

 

Y

 

 

	наклонная

 

 

 

Рисунок 2. Рисунок 3. Рисунок 4.

 

 

6.Интервалы монотонности. Экстремумы.

1) находим y^/(x);

2) находим критические точки из условия:

или не существует.

3) исследуем знак производной слева и справа от критических точек:

если непрерывна и на (a, b), то возрастает,

если 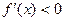, то убывает.

Если производная при переходе через критическую точку х₀ меняет свой знак с «+» на «-», то х₀ – точка максимума, а если с «-» на «+» - точка минимума функции.

 

7. Интервалы выпуклости и вогнутости. Точки перегиба.

График функции называется выпуклым на (a, b), если он расположен ниже (рис.5) любой своей касательной на этом интервале и вогнутым на (a, b), если он расположен выше (рис.6) любой своей касательной на этом интервале:

 

 

 

 

Рис.5. Рис.6.

а) находим ;

б) ищем критические точки второго рода – точки, в которых вторая производная равна нулю или не существует;

в) исследуем знак второй производной слева и справа от критических точек второго рода:

если функция дважды дифференцируема на и , то график функции на этом интервале вогнутый (выпуклый).

Точка графика непрерывной функции, отделяющая выпуклую часть от вогнутой, называется точкой перегиба графика функции.

г) ищем точки перегиба графика функции:

если при переходе через х₀ вторая производная меняет свой знак, то в точке с абсциссой х₀ график функции имеет точку перегиба.

8. При необходимости ищем несколько дополнительных точек.

9. Строим график функции.

Замечание. Рекомендуем начать построение графика функции со второго пункта, предложенного плана.

 

I.Исследовать функцию и построить ее график: .

1) 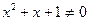при х , так как D=1-4=-3<0.

;

2) найдем точки пересечения графика с осями координат:

x=0, y=1;

y=0, x=- 0,5;

3) - функция общего вида;

4) функция непрерывна на , точек разрыва нет;

5) вертикальных асимптот нет.

Наклонные асимптоты:

,

.

Следовательно, y=0 – горизонтальная асимптота;

6) исследуем функцию на возрастание и убывание.

 

;

 

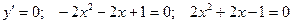- критические точки.

Исследуем знак производной слева и справа от этих точек:

-

 

- точка минимума; y_min≈ ,

- точка максимума; .

7)

Критические точки второго рода найдем из уравнения: ;

;

 

Исследуем знак второй производной слева и справа от этих точек;

 

- абсциссы точек перегиба графика функции, т.к. вторая производная меняет знак.

- ординаты точек перегиба графика функции.

 

8) На основании проведенных исследований построим график функции (рис.7):

Рис.7.

II.Исследовать функцию: .

1) , ;

2) найдем точки пересечения графика с осями координат:

x=0, y=1 - с осью ОY,

y=0, x=1 - c осью ОХ;

3) функция общего вида, так как ее область определения не симметрична относительно начала координат;

 

4) х=-1 – точка разрыва второго рода, так как

5) а) х=-1 вертикальная асимптота, так как х=-1 – точка разрыва второго рода;

б) наклонные асимптоты:

.

Следовательно y=0 – горизонтальная асимптота;

 

6) исследуем функцию на возрастание и убывание:

 

- критические точки.

 

Исследуем знак производной слева и справа от этих точек:

 

х=1 - точка минимума; y_min=y(1)=0,

x=5 - точка максимума; y_max=y(5)= ;

7) исследуем функцию на выпуклость – вогнутость.

Критические точки второго рода найдем из уравнения:

;

Исследуем знак второй производной слева и справа от этих точек:

- абсциссы точек перегиба графика функции.

- ординаты точек перегиба графика функции.

 

 

Литература [1, 2]

Вопросы для самопроверки:

1. Сформулируйте определение производной.

2. Какой механический смысл второй производной?

3. Сформулируйте правило Лопиталя.

4. Сформулируйте необходимое и достаточное условия экстремума.

5. Сформулируйте необходимое и достаточное условия существования точки перегиба.

 

 

Тема 5. Первообразная

Неопределенный интеграл, его свойства. Таблица основных интегралов. Непосредственное интегрирование. Интегрирование по частям и подстановкой.