 |
|
Похибки прямих вимірювань.
Нехай в результаті повторюваних вимірювань фізичної величини маємо послідовні значення
х1, х2, ..., хj , ...,хn.
Подамо результати n вимірювань, як відхилення виміряного від істинного значення фізичної величини xіст (далі просто х), у вигляді
Dх1 = х1 –х; Dх2 = х2 –х; ... , Dх j = х j –х; ..., Dх n = х n –х.
Підсумовуючи члени та розділивши їх на кількість вимірювань, дістанемо
де 
– середнє арифметичне значення вимірюваної величини.
При великій кількості вимірювань випадкові відхилення Dхі, однакові за модулями, але з різними знаками, зустрічаються однаково часто. Тому
Тоді х = 
. Отже при n → ∞ істинне значення фізичної величини дорівнює середньому арифметичному (звичайно, при цьому немає систематичних похибок).
У реальній метрологічній практиці число вимірювань n є скінченою величиною. Через це завдання теорії обробки результатів вимірювань зводиться до оцінки ступеня наближення вимірюваного значення до істинного.
Повне описання появи випадкових подій здійснюється за допомогою функції розподілу. Аналогічно використовується і функція розподілу випадкових похибок.
Досвід обробки результатів вимірювань показує, що розподіл похибок описується різними законами. Проте досить часто для опису розподілу випадкових похибок використовується нормальний закон розподілу (закон Гауса)
,
де 
– густина імовірності випадкової величини х,тобто імовірність віднесена до величини відповідного інтервалу Δх; Δх – відхилення від істинного значення;σ2 – дисперсія генеральної сукупності. Генеральною сукупністюназивається множина можливих значень вимірювань хі або можливих значень похибок Dхі.
Закон Гауса знаходить широке застосування в теорії похибок. Це зумовлено такими причинами:
1) для великої кількості вимірювань різні за модулем похибки зустрічаються однаково часто;
2) малі за модулем похибки зустрічаються частіше, ніж великі, тобто імовірність появи похибки тим менша, чим більше її абсолютне значення;
3) похибки вимірювань становлять неперервний ряд значень.
На рис. 1 наведено форму кривої Гауса для трьох значень σ. Початок координат розміщено в точці з нульовою похибкою. Для нормального закону розподілу є характерною його симетрія (при великій кількості вимірювань появи випадкових похибок, які рівні за розміром, але різні за знаком, - рівноймовірні) і монотонність зменшення густини імовірності (поява великих випадкових похибок малоймовірна). Права і ліва частини кривої Гауса асимптотично наближаються до осі абсцис.
Чим менше σ, тим вища крива розподілу і навпаки. Із збільшенням σ зростає розкид відліків, тобто точність вимірювання зменшується. Величина σ є основним параметром, який визначає вид кривої розподілу похибок вимірювання. Кожному з відліків відповідає точка по осі Δх.
Зміст функції Гауса такий. Площа фігури, обмеженої кривою Гауса, віссю х та прямими, паралельними вісі ординат, з координатами точок 
і 
(заштрихована площа на рис.1) чисельно дорівнює густині ймовірності з якою довільний вимір попадає в інтервал 
. Вся площа під кривою Гауса дорівнює одиниці.
Для оцінки величини випадкової похибки є кілька способів.
Найбільш поширеною є оцінка за допомогою середньої квадратичної (або стандартної) похибки (Sn)
Згідно з означенням
.
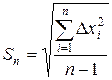Якщо число вимірювань дуже велике, то випадкова величина Sn прагне до деякої сталої величини σ, яку називають статистичною границею Sn. :
Ця границя, власне, і є середньою квадратичною похибкою.
Для оцінки точності результату виміряного значення фізичної величини використовують такі характеристики: довірчий інтервал та граничну (надійну) похибку середнього арифметичного.
Довірчий інтервал – це інтервал ( 
, 
), який містить істинне значення хіст виміряної фізичної величини х із заданою імовірністю α, яка називається надійною імовірністю (або коефіцієнтом надійності).
Надійністю результату серії вимірювань називають вірогідність 
того, що істинне значення х вимірюваної величини потрапляє в даний довірчий інтервал; виражається або в частках одиниці, або у відсотках.
Чим більше довірчий інтервал, тим з більшою надійністю шукана величина х потрапляє в цей інтервал. Природно, що величина залежить від числа n проведених вимірювань, а також від похибки, що задається 
.
Так, при 
вибираючи рівним 
, ми набудемо значення 
. Ймовірність того, що будь-яке значення вимірюваної величини буде лежати в інтервалах 
, 
дорівнює, відповідно 95% і 99%. Значення 0,99 рекомендується брати для випадків, коли вимірювання не можна повторити.
Таким чином, величина характеризує ступінь впливу випадкових похибок на результати вимірювання: чим менше , тим точніше проведене вимірювання.
Обробка результатів серії вимірювань зводиться до можливо точнішого знаходження 
і . Величину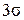 
звичайно приймають за граничну абсолютну похибка окремого вимірювання (іноді замість 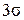беруть абсолютну похибка вимірювального приладу).
Якщо при вимірюванні абсолютна похибка більша за 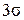, то це вимірювання слід віднести до грубих похибок або промаху. Величину 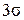, звичайно, приймають за граничну абсолютну похибку окремого вимірювання.
Оскільки неможливо виконати дуже велике число вимірювань, то виникає питання: як змінюється надійність при зміні числа вимірювань? Залежність ця складна і не виражається в елементарних функціях. Існують спеціальні таблиці коефіцієнтів Стьюдента, по яких можна визначити, в скільки разів потрібно збільшити стандартний довірчий інтервал, щоб при певному числі вимірювань n одержати задану надійність (табл. 1).
Оцінка стандартного відхилення 
проводиться за формулою:
Тоді Δ – гранична похибка, яка дорівнює половині надійного інтервалу, розраховується за формулою
,
де 
– нормований коефіцієнт Стьюдента, який залежить від надійної імовірності та кількості вимірювань.
Результати вимірювань записуються у вигляді
Таблиця 1. Таблиця коефіцієнтів Стьюдента
| Число вимірювань | Надійність | |||||||
| 0.5 | 0,6 | 0,7 | 0.8 | 0.9 | 0,95 | 0.98 | 0.99 | |
| 1,00 | 1,38 | 2,0 | 3,1 | 6,3 | 12.7 | 31,8 | 636,6 | |
| 0,82 | 1,06 | 1,3 | 1,9 | 2,9 | 4,3 | 7,0 | 31.6 | |
| 0,77 | 0,98 | 1,3 | 1.6 | 2.4 | 3,2 | 4,5 | 12,9 | |
| 0,74 | 0,94 | 1,2 | 1,5 | 2,1 | 2,8 | 3.7 | 8,6 | |
| 0,73 | 0,92 | 1,2 | 1,5 | 2,0 | 2.6 | 3,4 | 6,9 | |
| 0,72 | 0.90 | 1.1 | 1.4 | 1.9 | 2.4 | 3,1 | 6,0 | |
| 0,71 | 0,90 | 1,1 | 1,4 | 1,9 | 2,4 | 3,0 | 5,4 | |
| 0.71 | 0,90 | 1,1 | 1,4 | 1.9 | 2,3 | 2,9 | 5,0 | |
| 0.70 | 0.88 | 1.1 | 1,4 | 1,8 | 2,3 | 2,8 | 4,8 | |
| 0,69 | 0,87 | 1.1 | 1.3 | 1,8 | 2.1 | 2,6 | 4,1 | |
| 0.69 | 0,86 | 1.1 | 1.3 | 1.7 | 2.1 | 2.5 | 3.9 | |
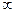
| 0,67 | 0,84 | 1,0 | 1,3 | 1,6 | 2,0 | 2,3 | 3,3 |
Декілька зауважень про розподіл Стьюдента. Як уже відмічалось, розподіл Стьюдента справедливий для малого числа вимірювань n ³ 2, що характерно як для техніки, так і для наукових досліджень. Із зростанням числа вимірювань розподіл Стьюдента прагне до нормального розподілу (фактично при n > 20). Математичного виразу розподілу Стьюдента ми не наводимо, зважаючи на його складність.
Характерним для розподілу Стьюдента є його незалежність від параметрів та σ нормальної генеральної сукупності, а також можливість оцінки при невеликомучислі вимірювань n < 20 похибки Δх = – хі за заданою надійною ймовірністю α або знаходження надійності вимірювання за заданим значенням Δх.
Розподіл Стьюдента дає також змогу встановити, що при досить великому n середнє арифметичне значення з імовірністю, як завгодно близькою до вірогідності, доволі мало відрізняється від істинного значення х.
Порядок обробки результатів вимірювань наступний:
- виконують n вимірювань і записують їх результати в таблицю;
- обчислюють 
;
- обчислюють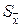 
і знаходять по таблиці коефіцієнт Стьюдента залежно від заданої надійності і числа вимірювань n.
Результат записують у вигляді
.
Це означає, що істинне значення вимірюваної величини 
знаходиться в інтервалі [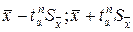 
] з надійністю .
Мірою точності результатів вимірювань є відносна похибка (в %):
·100%.
Зворотну їй величину 
називають точністю вимірювань.
Використовуючи таблицю коефіцієнтів Стьюдента, часто вирішують і зворотну задачу: по відомій абсолютній похибки вимірювального приладу і заданій величині надійності визначають необхідне число вимірювань в серії.
Приклад. Нехай проведено 6 вимірювань товщини пластинки штангенциркулем. Результати вимірювань наведено в табл. 2. Провести обробку результатів вимірювання при α = 0.95.
Обробку результатів виконуємо у такій послідовності:
а) вважаємо, що систематичних похибок немає;
Таблиця 2. Результати вимірювання
| Номер спостереження | Результати спостереження, dj , мм | Відхилення від середнього арифметичного, Δdі , мм | Квадрат відхилення від середнього арифметичного Δdj 2, мм2 |
| 30.1 | +0.1 | 0.01 | |
| 30.0 | – | – | |
| 30.1 | +0.1 | 0.01 | |
| 29.8 | –0.2 | 0.04 | |
| 29.9 | –0.1 | 0.01 | |
| 30.1 | +0.1 | 0.01 |
б) обчислюємо середнє арифметичне 
= 30,0 мм
в) обчислюємо значення Δdі , Δdі2 і записуємо їх у таблицю;
г) обчислюємо оцінку середнього квадратичного відхилення результату спостереження:
.
Максимальна можлива похибка Sdmax . Її ми беремо такою, що дорівнює 3Sd (за правилом трьох сигма вважають, що значення 3σ є межею випадкового відхилення спостереження або просто максимальним відхиленням; йому відповідає імовірність α = 0,997 (практично дорівнює одиниці); зважаючи на це, одним з критерію промаху є значення відхилення окремого спостереження, більше 3 σ). Отже, результати всіх шести спостережень слід вважати надійними, оскільки вони задовольняють правило трьох сигма, і промахів немає;
д) обчислюємо оцінку середнього квадратичного відхилення результату вимірювання за формулою
;
е) обчислюємо надійні межі випадкової похибки результату вимірювання при α = 0.95.
При n = 6 і α = 0.95 коефіцієнт Стьюдента – 2.57. Тоді Δd = 2.57· 0.04 ≈ 0.1 мм.
Результат вимірювань записуємо у вигляді d = 30.0 ± 0.1 мм.
Відносна похибка
.
Якщо ж зроблено тільки одне вимірювання, то точність вимірювання фізичних величин в цьому разі (якщо воно виконано ретельно) характеризується точністю вимірювального приладу.