Главная | Обратная связь

Обчислення з наближеними числами

Маючи результати вимірювань можна визначити вірні, сумнівні і невірні цифри. Якщо похибка містить в собі десятки, то число десятків буде сумнівним.

Наприклад, в серії вимірювань одержано: м, 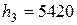м, м, м. У остаточному результаті h = (5390 ± 30)м похибка містить в собі десятки метрів. Цифри, що стоять зліва від сумнівної, – вірні; що стоять праворуч від сумнівної – невірні (вони повинні бути відкинуті як в початкових даних, так і в остаточному результаті). У розглянутому прикладі остаточний результат слід записати так: h = (5390 ± 30)м.

До значущих відносять всі вірні і сумнівні цифри; до незначущих – нулі на початку десяткових дробів, менших 1; нулі в кінці числа, що замінили цифри, відкинуті після округлення; невірні цифри, якщо вони з якихось причин не відкинуті.

Приклад. Числа 584 ± 6; 0.00456 ± 0.00002; 0.002442 ± 0.00003 містять по три значущі цифри. У числі 5628 всі цифри значущі, оскільки помилка не вказана. Якщо дане число 1,000000 ± 0,000003, то в ньому останній нуль сумнівний, тому всі інші нулі в цьому числі значущі.

1. При складанні і відніманні розряд сумнівної цифри суми співпадає зі старшим із розрядів сумнівних цифр всіх доданків.

Тому при складанні чисел потрібно:

а) у всіх доданків визначити розряди сумнівних цифр і знайти з них найстарший;

б) всі доданки округляти до цього розряду або зберегти ще один, наступний за сумнівним (запасна цифра);

в) скласти доданки, причому сумнівна цифра суми співпадає із старшим з розрядів сумнівних цифр всіх доданків.

Приклад. Скласти .

Всі запропоновані числа містять значущі числа. У першого числа сумнівна цифра – десятки; у другого – одиниці; у третього – в розряді десятих часток, у четвертих – в розряді стотисячних. Старший розряд – десятки. Округлення проводять до старшого розряду — десятків. Тоді

.

Останній доданок відкидають зовсім (у ньому немає ні десятків, ні одиниць).

2. Результат множення і ділення містить стільки значущих цифр, скільки їх є в початковому даному з якнайменшою кількістю значущих цифр. Тому при множенні або розподілі чисел:

а) представляють початкові числа у вигляді, коли кома стоїть після першої цифри, а всі значущі цифри перемножують на множник десять у відповідній степені;

б) зі всіх початкових чисел знаходять число, де якнайменша кількість значущих цифр;

в) всі початкові числа округляють так, щоб всі вони містили таку кількість значущих цифр, скільки їх було в числі з якнайменшою їх кількістю (іноді беруть для вірності ще по одній запасній цифрі);

г) виконують дію над числами, які отримано після округлення, не звертаючи уваги на кому і множник десять в деякій степені; в результаті залишають стільки значущих цифр, скільки їх було в числі з якнайменшою їх кількістю; виконують операції множення (ділення) коефіцієнтів десять в деякій степені;

д) записують результат.

Приклад. Нехай необхідно помножити 981.17 на 0.314

Представимо співмножники як 9.8117×10² і . Після округлення маємо

і після множення

.

Помножимо коефіцієнти . Остаточний результат: .