Главная | Обратная связь

Визначення моменту інерції махового колеса

Мета роботи: використовуючи закон збереження механічної енергії, експериментально визначити момент інерції махового колеса і порівняти отриманий результат з розрахунком по теоретичній формулі.

Тверде тіло являється системою матеріальних точок, відстань між якими при русі не змінюється. При русі навколо нерухомої вісі всі матеріальні точки, що утворюють тіло обертаються з однаковою кутовою швидкістю w.

Нехай r_i – відстань і-тої матеріальної точки до вісі обертання, а m_i – її маса. Тоді лінійна швидкість цієї точки , а момент імпульсу відносно вісі обертання . Момент імпульсу L твердого тіла складається з моментів імпульсу всіх утворюючих це тіло матеріальних точок:

,

де – момент інерції твердого тіла відносно вісі обертання.

Під дією прикладених до тіла зовнішніх сил його момент імпульсу 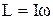змінюється зі швидкістю

,

де – сума моментів зовнішніх сил, прикладених до тіла:

.

Тут – момент сил відносно вісі обертання j-ої зовнішньої сили, прикладеної до тіла; F_j – проекція цієї сили на площину, перпендикулярну до вісі обертання тіла; – плече цієї сили.

Момент інерції тіла залежить від вибору вісі обертання. Але це не значить, що для всілякої нової вісі момент інерції І необхідно обчислювати спочатку. Момент інерції твердого тіла І відносно вісі, яка паралельна вісі, що проходить через центр інерції тіла, дорівнює (теорема Гюйгенса-Штейнера):

,

де І₀ – момент інерції тіла відносно вісі, що проходить через центр інерції тіла, m – маса твердого тіла, а – відстань між осями.

Моментом інерції називають фізичну величину, що характеризує інерційні властивості тіла в обертальному русі. Тобто момент інерції є аналогом маси в поступальному русі.

Момент інерції суцільних тіл, що мають густину , можна обчислити інтегруванням: .

Кінетична енергія обертального руху визначається за формулою:

.

Ця формула справедлива лише у випадку, коли тіло обертається навколо нерухомої вісі. Якщо тіло рухається як ціле і обертається, то його кінетичну енергію можна представити у вигляді суми кінетичних енергій поступального руху центра мас тіла і обертального руху навколо вісі обертання (теорема Кьонінга):

,

де V_C – швидкість центра мас (центра інерції) твердого тіла; І₀ – момент інерції тіла відносно вісі, що проходить через центр мас тіла.

Момент інерції махового колеса визначають на установці, яка складається з махового колеса зі шківом, насадженого на вал, лінійки і тягарця (рис.8 ). Вал закріплений у двох підшипниках. На вал 3 намотується нитка. До її кінця прикріплюють тягарець 4 масою m. Під дією тягарця шків разом з валом і маховим колесом рівноприскорено обертається. На характер обертального руху впливають значення моменту інерції махового колеса, моменту інерції шківа, моменту інерції вала та сили тертя в підшипниках. Вал і шків вибира­ють такими, щоб вони мінімально впливали на характер обертального руху і не вносили істотних змін в його характер. При падінні тягарця його потенціальна енергія , де h – висота підняття тягарця, перетворюється в кінетичну енергію поступального руху тягарця, в кінетичну енергію обертального руху махового колеса і витрачаєть­ся на виконання роботи подолання сил тертя.

Кінетична енергія по­ступального руху тягарця визначається за формулою

,

де v – швидкість тягарця. Кінетична енергія обертального руху системи визначається за формулою

,

де І, w – момент інерції і кутова швидкість всіх обертаючихся елементів.

Якщо знехтувати силами тертя в підшипниках і опором повітря, то згідно закону збереження енергії можна записати:

.

Рух тягарця є рівноприскореним з прискоренням а, тому є справедливим наступні вирази: , і, як результат, . Так, як нитка намотана на вал, то швидкість поступального руху нитки і, звісно, тягарця завжди дорівнює лінійній швидкості точок, що лежать на поверхні валу. Тому і , де r – радіус вала.

З врахуванням цього закон збереження можна переписати у вигляді

,

звідки момент інерції системи

.

Якщо колесо зняти, то момент інерції утвореної системи буде визначатися тією ж формулою, але час t₀ опускання тягарця на висоту h буде іншим.

Момент інерції самого колеса можна визначити як різницю

або , (1)

де t – час опускання тягарця при надітому на шків колесі, t₀ – час опускання тягарця без колеса.

Розглянемо випадок, коли силами тертя не можна нехтувати. В цьому випадку закон збереження і перетворення енергії має вигляд

,

де – робота подолання сил тертя; F — сила тертя. Силу тер­тя визначимо з таких міркувань. Обертаючись за інерцією, махове колесо підніме тягарець на висоту , система матиме потенціальну енергію . Різниця потенціальних енергій дорівнюватиме роботі подолання сил тертя , звідки

.

Підставивши вирази для в закон збереження енергії, матимемо формулу для визначення моменту інерції системи для цього випадку

.

При знятті колеса зі шківу момент інерції утвореної системи буде визначатися тією ж формулою. Момент інерції самого колеса в цьому випадку можна визначити як різницю

або , (2)

де t, t₀ – час опускання тягарця при надітому на шків колесі і без нього; h₁, h₂ – висота підіймання тягарця за інерцією з колесом і без нього на шківі.

Момент інерції колеса можна розрахувати теоретично інтегруванням елементарних циліндричних шарів від R₁ (зовнішній радіус) до R₂ (внутрішній радіус колеса). Результат такого розрахунку дає наступний вираз для моменту інерції махового колеса:

, (3)

де М – маса колеса.