 |
|
Похибки непрямих вимірювань.
Як бути, якщо х визначається не прямим вимірюванням, а непрямим, тобто за наслідками вимірювань інших величин у і z? Хай х є деякою функцією у і z, тобто
.
Тоді якнайкраще значення при оцінці х рівне
,
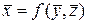де 
і 
середні арифметичні значення. Як же знайти, якщо відомі 
і 
? Оскільки самі величини у і z знаходяться шляхом прямих вимірювань, то їх похибки і можна оцінити по формулах для прямих вимірювань.
Помітимо, перш за все, що 
. Отже, простою оцінкою для 
є різниця
тобто помилка непрямого вимірювання знаходиться через помилки прямих вимірювань за правилом диференціювання. Часто цієї оцінки виявляється досить.
Точнішим є наступний вираз:
де 
і – частинні похідні по у і z, узяті при значеннях, 
, 
.
Часто зручно виражати точність, з якою знайдено х, через відносну похибка 
. За визначенням
,
де 
– розраховують через і .
Помітимо, що, виходячи з визначення відносної похибки результат вимірювань величини х, можна записати у вигляді
, оскільки 
Розглянемо практично важливий випадок, коли х є степеневою функцією у і z:
,
(m і n можуть бути цілими або дробовими, більше або менше нуля).
Відносна похибка рівна
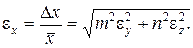
Звідси випливає важливий висновок: при вимірюваннях необхідно найточніше визначити значення величини, що входить в розрахункову формулу з найбільшим по модулю показником ступеня.
Приведемо прості випадки розрахунку граничних похибок результату непрямого вимірювання величини Y.
1. Нехай Y = А + B, а граничні абсолютні похибки прямого вимірювання величин А і B відповідно рівні DA і ΔΒ (це або похибки вимірювальної апаратури, або результат розрахунку).
Тоді
Y±DY = (А±DА) + (В±DВ).
Очевидно, найбільш невигідний випадок той, коли DA і ΔΒ будуть однакові по знаку, наприклад +ΔА і +ΔΒ, тоді гранична абсолютна похибка результату дорівнює ±ΔY= DA+ΔΒ, а гранична відносна похибка
2. Нехай Y = АВ, тоді
Y ± ΔY = (А ± DA) (Y ± ΔΒ) = АВ± АDВ ±BΔA+DА×DB
Вважаючи DA×ΔΒ << 1, нехтуємо малим доданком. Одержуємо
3. Нехай Y = An. Тоді 
Гранична відносна похибка рівна
а гранична абсолютна похибка
.
4. Нехай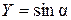 
. Тоді
.
| Таблиця 3 Відносна похибка функції | ||
| № | Вид функції | Гранична відносна похибка |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
| 
| |
|  
| |
| 
| |
 
| 
| |
|
|
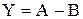
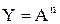
Покладемо, що 
мала. В цьому випадку 
. Отже,
,
і тоді
.
В таблиці 3 наведено формули розрахунку відносних граничних похибок фізичних величин, що виражені найбільш поширеними функціями.
Якщо в розрахункові формули входять константи, наприклад число π, фізичні постійні, табличні дані, то вони беруться з такою точністю, щоб число значущих цифр в них було на одиницю більше, ніж число значущих цифр в значеннях вимірюваних величин. Тоді константи практично не вносять похибок в результат вимірювань.