 |
|
ТРИЗ-задание 19. Самодельный калориметр
В лабораторных работах калориметрические измерения можно производить либо в учебном калориметре (два стаканчика, вставленных друг в друга), либо в бытовом термосе. Недостатки этого оборудования – относительно высокая стоимость (десятки и сотни рублей) и высокая собственная теплоёмкость. «Идеальный калориметр» имеет нулевую стоимость и теплоёмкость. Воспользуемся вещественно-полевыми ресурсами, а именно надсистемными, «копеечными» ресурсами вещества. Задание: необходимо изготовить самодельный калориметр из верхней и нижней части пластиковой бутылки 1,5 л и алюминиевой банки из-под газированной воды объёмом 0,33 л (вместо алюминиевой банки можно взять одноразовый пластиковый стаканчик).
10. Адиабатический процесс
Адиабатический процесс – это процесс, протекающий без теплообмена с внешней средой. Тогда из первого начала термодинамики следует
dQ = 0 Þ dU + dA = 0 Þ dА = – dU . (52)
Таким образом, при адиабатическом расширении газ совершает работу за счет убыли его внутренней энергии. Это обозначает, что его температура понижается (а если газ адиабатически сжимать, то он нагревается). Поэтому при адиабатическом процессе изменяются все три параметра – p, V, T. Следовательно, он не может называться изопроцессом.
Из уравнения (52) можно получить формулу для адиабатической работы n молей газа:
. (53)
Найдем уравнение адиабаты для произвольного числа молей n. Для чего используем первое начало термодинамики:
dA + dU = 0;
p dV + n CV dT = 0. (54)
Исключим из уравнения (54) температуру, продифференцировав уравнение Менделеева-Клапейрона:
pV = n RT Þ p dV + V dp = n R dT Þ
Þ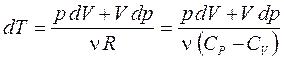 
. (55)
Подставим формулу (55) в уравнение (54), приведем выражение к общему знаменателю и учтем то, что дробь равна нулю, если её числитель равен нулю (число молей n при этом сокращается):
p CP dV – p CV dV + p CV dV + V CV dp = 0 (делим на pVCV),
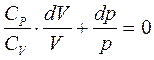(интегрируем),
|
g ln V + ln p = ln (const)
. (56)
Уравнение (56) является уравнением Пуассóна (адиабаты), а величина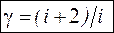 
> 1 является показателем адиабаты.
Изобразим изотерму и адиабату на одном графике. Для этого продифференцируем их уравнения:
T = const, pV = const, p dV + V dp = 0 Þ 
.
Q= const, pVg= const,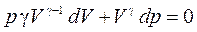 
Þ 
.
Следовательно, тангенс угла наклона (производная) адиабаты в g раз больше, чем у изотермы: адиабата идет круче, поскольку при расширении газа давление уменьшается не только за счет увеличения объёма, но и за счет уменьшения температуры (рис. 28).
Можно найти и другие формы записи уравнения адиабаты, подставив в уравнение (56) давление или объём, найденные из уравнения Менделеева-Клапейрона (pV = RT):
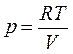® (56) Þ 
, 
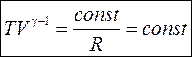. (57)
® (56) Þ 
, 
.
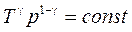Возведем последнее уравнение в степень (1/g):
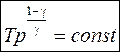. (58)
Изотермический и адиабатический процессы являются идеализированными: изотермический требует идеального теплового контакта с окружающей средой, а адиабатический – идеальной теплоизоляции.
Близкими к адиабатическому являются быстропротекающие процессы, когда теплообменом можно пренебречь.
Найдем работу при адиабатическом изменении объёма газа. Пусть при этом р1 – начальное давление газа, а V1 – его начальный объём.
Þ 
.
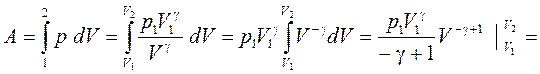
. (59)
Если, например, по условию задачи даны температуры, то в уравнении (59) можно произвести замены p1V1 = (m/M) RT1 и (V1/V2)g-1 = T2/T1 (последнее следует из уравнения TVg–1 = const). В результате получим
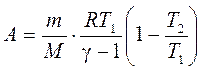. (60)
ТРИЗ-задание 20. Лампа Алладина
В старом кинофильме «Волшебная лампа Алладина» на экране нам показывают газообразного джина высотой 10–20 м. По закону Архимеда плотность джина должна быть равна плотности воздуха, чтобы он мог быть в воздухе неподвижным (а не всплывать, как воздушный шар). Предполагая, что количество молекул джина в газообразном состоянии и помещенного внутрь лампы одинаково, оцените массу волшебной лампы с джином. Если в результате расчётов масса лампы с джином окажется слишком большой, то, используя ТРИЗ, предложите 10 разных научно-фантастических гипотез, объясняющих то, каким образом большой джин мог появляться из маленькой лёгкой лампы. В одной из таких гипотез используйте адиабатический процесс.
11. Политропический процесс
Политропическими называются процессы, при которых теплоёмкость тела остается постоянной (C = const).
Изохорный, изобарный, адиабатический и изотермический процессы являются частными случаями политропического.
В самом деле:
приV = const 
;
приp = const 
;
при Q = const, dQ = 0 
;
при T= const, dT= 0 
(при изотермическом процессе сообщение телу любого количества теплоты не приводит к изменению температуры тела).
Найдем уравнение политропы. Для простоты проведем расчёт для 1 моля газа (если проводить расчет для произвольного числа молей, то число молей n при этом сокращается). Воспользуемся определением теплоёмкости: C = dQ/dT Þ dQ = C dT.
Из первого начала термодинамики следует:
dQ = dU + dA,
C dT = CV dT + p dV,
(C – CV) dT – p dV = 0. (61)
Аналогично тому, как это делалось при выводе уравнения адиабаты, исключим из уравнения (61) температуру:
pV = RT Þ p dV + V dp = R dT Þ
Þ 
. (62)
Подставим формулу (62) в уравнение (61), приведём выражение к общему знаменателю и учтём то, что дробь равна нулю, если её числитель равен нулю:
C p dV + CV dp – CV p dV – CV V dp – CP p dV + CV p dV = 0,
(C – CP) p dV + (C – CV) V dp = 0 [делим на (C – CV) pV],
(63)
Введём показатель политропы как
. (64)
Продолжаем решать уравнение (63):
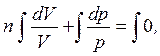
n ln V + ln p = ln (const),
. (65)
Уравнение (65) является уравнением политропы в координатах (p, V). Уравнения политропы в других координатах получаются аналогично тому, как это делалось для уравнения адиабаты (а можно индекс g в уравнениях адиабаты заменить на n).
В рассмотренных уравнениях переменная С – это теплоёмкость газа в конкретном процессе. Поэтому получим из общего уравнения (65) его частные случаи (процессы):
адиабатический С = СА = 0 ® (64) Þ
Þ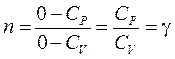 
® (65) Þ pVg= const;
изотермический С = СТ = ¥ ® (64) Þ
Þ 
® (65) Þ pV= const;
изобарический С = СР ® (64) Þ
Þ 
® (65) Þ pV0= p×1 = p= const;
изохорический С = СV ®(64) Þ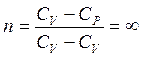 
.
Из уравнения (65) извлечем корень n-й степени и получим:
Подставив в последнее уравнение величину n = ¥, получим:
p0V = 1×V = V = const.