 |
|
Энтропия. Второе и третье начала термодинамики
Система находится в термодинамическом равновесии, если макроскопические величины, определяющие её состояние (p, V, T), остаются постоянными (нет процессов теплопроводности, диффузии, химических реакций, фазовых переходов и т.п.). Будучи выведенной из состояния равновесия внешними воздействиями, система самопроизвольно возвращается к термодинамическому равновесию.
При обратимых процессах система возвращается в исходное состояние так, что как в самой системе, так и в окружающей среде не остается никаких изменений. Обратимым является процесс, для которого возможен обратный переход из конечного состояния в начальное через те же промежуточные состояния, что и в прямом процессе. Обратимыми являются все движения, рассматриваемые в механике, кроме тех, в которых участвуют диссипативные силы. В молекулярной физике большинство процессов необратимо и имеет односторонний характер (переход тепла от горячего тела к холодному, распространение газа на весь объём, смешивание двух различных газов при диффузии).
Возьмем уравнение первого начала термодинамики:
dQ = dU + dA = n CV dT + p dV. (66)
Найдем из уравнения Менделеева-Клапейрона давление p = nRT/V и подставим его в уравнение (66):
 .
.
Разделим обе части этого уравнения на Т:

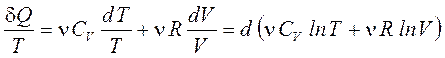 . (67)
. (67)
Правая часть равенства (67) представляет собой полный дифференциал, следовательно, и левая часть также является полным дифференциалом.
Функция состояния, полный дифференциал которой равен dQ/T, называется энтропи́ей и обозначается буквой S:
 . (68)
. (68)
Свойства энтропии:
Энтропия замкнутой системы, совершающей обратимый цикл, не изменяется dSОБР = 0, или S = const.
В ходе необратимого процесса энтропия замкнутой системы возрастает dSНЕОБР > 0 и достигает максимального значения в равновесном состоянии (т.е. S2 > S1).
Второе начало термодинамики: энтропия замкнутой системы при любых происходящих в ней процессах не убывает dS ³ 0. Знак (>) соответствует необратимому процессу, а знак (=) - обратимому.
Если же система не замкнута, т.е. может обмениваться теплотой с окружающей средой, то энтропия может вести себя любым образом (увеличиваться, уменьшаться, не изменяться).
Энтропию можно также определить статистически с помощью формулы Больцмана: S = k ln W , где k – постоянная Больцмана; W – статистический вес или термодинамическая вероятность состояний. Для величины W в разных учебниках приводятся разные определения, например:
W – число различных равновероятных микросостояний (всевозможных распределений частиц по координатам и скоростям), которые реализуют данное макросостояние (p, V, T);
W – число способов, реализуя которые система может прийти к данному равновесному состоянию.
В равновесном состоянии макропараметры (p, V, T) постоянны, однако микропараметры (скорости, координаты, импульсы частиц) постоянно меняются. Поэтому число W очень огромно.
Состояние, которое осуществляется многими способами, называется беспорядочным, или случайным. Следовательно, энтропия является мерой беспорядка в системе. Сообщение системе количества теплоты приводит к усилению хаотического движения молекул, увеличивает (энтропию) степень беспорядка в системе.
При абсолютном нуле Т = 0 движения нет, и все атомы тела закреплены в определенных местах. Существует только одно микросостояние W = 1. Следовательно, энтропия равна нулю: S = k ln 1 = 0. Отсюда следует третье начало термодинамики (теорема Нернста): энтропия любого тела стремится к нулю при стремлении температуры к нулю, или при Т = 0 в любом процессе DS = 0.
Всякий естественный процесс всегда протекает так, что система переходит в состояние с более высокой степенью беспорядка, так как такое состояние характеризуется большей термодинамической вероятностью. С этим связана и необратимость тепловых процессов: беспорядок в системе увеличивается. Любой вид энергии (механической, электрической…) в конечном итоге переходит в тепловые (хаотические) колебания атомов и молекул.
Второе начало термодинамики, установленное для замкнутых систем на Земле, не может быть распространено на всю бесконечную Вселенную. Иначе можно прийти к выводу, что температуры всех тел во Вселенной станут одинаковыми. Энтропия достигнет своего предельного – максимального – значения, и наступит абсолютно равновесное состояние, в котором никакие процессы уже невозможны. Все виды энергии перейдут в тепловой вид, при этом все формы движения, кроме хаотического теплового, должны прекратиться. Наступит «тепловая смерть Вселенной».
Из определения энтропии следует, что площадь под кривой на диаграмме (T, S) численно равна количеству теплоты Q12, полученному телом в ходе процесса 1 ® 2 (рис. 29):

 dQ= T dS,
dQ= T dS, 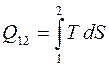 . (69)
. (69)
При T = const Q12 = T (S2 – S1).
Как видно из рис. 29, количество теплоты (площадь под кривой) зависит от вида перехода 1 ® 2. Следовательно, количество теплоты Q не является функцией состояния, а её элементарное изменение dQ не является полным дифференциалом.