 |
|
Наслідки з основного рівняння кінетичної теорії ідеального газу.
а) Закон Бойля – Маріотта
Скористаємося рівнянням Клаузіуса у вигляді:
Врахувавши, що 
, тому отримаємо 
=> 
Закон Бойля – Маріотта описує ізотермічний процес, тобто процес, що протікає при постійний температурі 
, тоді 
.
По друге, закон Бойля – Маріотта має місце для газу, кількість молекул якого незмінна, тобто 
Тоді 
- закон Бойля – Маріотта.
Добуток тиску газу на об’єм при даній масі газу і при постійній температурі є величина постійна.
Виникає питання:
в чому полягає фізичний зміст закону Бойля – Маріотта?
Для відповіді на поставлене питання перевіримо розмірність цього закону в СІ.
Отже, з точки зору фізики закон Бойля – Маріотта показує, що при ізотермічному процесі внутрішня енергія газу не змінюється.
б) Середня кінетична енергія поступального руху молекули ідеального газу.
Скористаємося основним рівнянням Клаузіуса в формі:
, де 
- молярний об’єм
Для молярного об’єму кількість молекул дорівнює числу Авогадро
(1)
Запишемо рівняння Клапейрона – Менделєєва для 1 моля газу:
(2)
Співставивши (1) і (2), отримаємо:
=> 
- постійна Больцмана
Отже,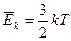 
(3)
З (3) слідує фізичний зміст постійної Больцмана:
вона показує, яку роботу здійснює 1 молекула газу, що рухається з деякою середньою швидкістю, при підвищені температури газу на 1 0К.
в) Число Лошмідта
Підрахуємо кількість молекул газу в одиницю об’єму. Для цього скористаємося основним рівнянням МКТ, що має вигляд:
Підставляючи сюди значення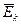 
з формули (3), отримаємо:
(4)
Тоді 
(5)
При однакових температурі і тиску всі газу містять в одиниці об’єму однакову кількість молекул. Кількість молекул, що міститься в 1 м3 газу за нормальних умов називається числом Лошмідта. За формулою (5) воно дорівнює
г) Середня квадратична швидкість руху молекул ідеального газу:
Виводячи основне рівняння МКТ ми позначимо середню квадратичну швидкість через 
. Тоді середня кінетична енергія
. З іншого боку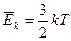
Тоді 
=> 
=> 
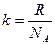
(6)
тобто для даного газу середня квадратична швидкість молекул пропорційна кореню квадратному з абсолютної температури і залежить тільки від неї.