 |
|
Модель «дуга – работа»
Построим математическую модель, которая позволит найти оптимальные значения продолжительностей работ при заданных продолжительности проекта, отношениях предшествования, верхних и нижних пределах продолжительности для каждой работы.
Для формулировки задачи линейного программирования введём следующие обозначения:
A – множество работ проекта,
– ранний срок наступления события,
– величина сокращения времени работы,
i = 1 – номер начального события сети,
i = n – номер конечного события сети,
– желательное время выполнения проекта,
– удельные затраты на сокращение работы (наклон),
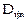– нормальное время выполнения работы,
– критическое время выполнения работы.
При данных обозначениях модель линейного программирования имеет вид:
(1)
(2)
(3)
(4)
(5)
Если m – число работ, n – число событий, то описанная модель имеет n+m переменных, m ограничений (2), m ограничений (3), одно ограничение (4) и n+m ограничений (5).
Если 
– оптимальный план, то 
– время, на которое следует сократить продолжительность работы (i,j).
– минимальная сумма дополнительных издержек, необходимая для сокращения времени выполнения проекта до величины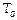 
.
Подставим теперь данные примера 5.1 в сформулированную математическую модель:
A: 
B: 
C: 
D: 
E: 
F: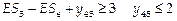 
Данная задача решается при значениях 
.
Например, при 
получим:
Ответ:
| T0 | Y12 | Y13 | Y24 | Y25 | Y34 | Y45 | F | |
| Сократили А | ||||||||
| Сократили А | ||||||||
| Сократили D | ||||||||
| Сократили D | ||||||||
| Сократили D | ||||||||
| Сократили D | ||||||||
| Сократили D и F |
Добавив в нашу модель прямые затраты при нормальной длительности (= 580) и косвенные затраты (145 ден. ед. в день), можно определить общие затраты для каждого значения 
или минимум общих затрат: 
.
Пошаговое решение:
| T0 | ||||||||
| F |
Минимизация общих затрат:
Ответ:
| T0 | Y12 | Y13 | Y24 | Y25 | Y34 | Y45 | F |
4.2.2. Модель «узел – работа»
Рис. 5.12
Обозначения:
A – множество работ проекта,
– множество предшественников для работы i,
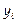– величина сокращения времени работы i,
– желательное время выполнения проекта,
– удельные затраты на сокращение работы i (наклон),
– нормальное время выполнения работы i,
– критическое время выполнения работы i.
При данных обозначениях модель линейного программирования имеет вид:
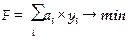(1)
(2)
(3)
(4)
(5)
Теперь для примера 4.1 получим:
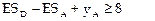
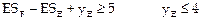
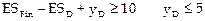
Данная задача решается при значениях 
.
Параметры поиска решения:
Ответ:
| T0 | YA | YB | YC | YD | YE | YF | F | ||
| Шаг 1 | |||||||||
| Шаг 2 | Сокращается А | ||||||||
| Шаг 3 | Сокращается А | ||||||||
| Шаг 4 | Сокращается D | ||||||||
| Шаг 5 | Сокращается D | ||||||||
| Шаг 6 | Сокращается D | ||||||||
| Шаг 7 | Сокращается D | ||||||||
| Шаг 8 | Сокращаются D и F |
Добавив в нашу модель прямые затраты при нормальной длительности (= 580) и косвенные затраты (145 ден. ед. в день), можно определить общие затраты для каждого значения или минимум общих затрат: 
.
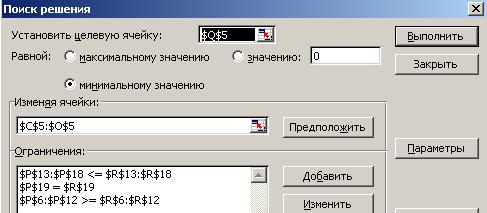
Пошаговое решение:
| T0 = | ||||||||
| F = |
Минимизация общих затрат:
Ответ:
| T0 | YA | YB | YC | YD | YE | YF | F |
 |
Тема 5.
