 |
|
Відстань від точки до прямої.
Завдання № 3. Знайдіть відстань від точки  до прямої
до прямої 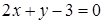 .
.
Розв'язок. Відстань знайдемо по формулі (2.10).
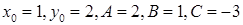 .
.
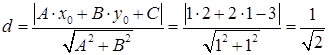
Відповідь:відстань дорівнює 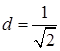 (лін. од.).
(лін. од.).
Завдання № 4. Знайдіть відстань від точки  до прямої
до прямої 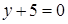 .
.
Розв'язок.  .
.
По формулі (2.10):
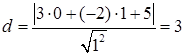 .
.
Відповідь:  (лін. од.).
(лін. од.).
Кут між двома прямими.
Завдання № 5. Знайти кут між прямими
 ,
,  .
.
Розв'язок.Кут між прямими знаходиться по формулі (2.3)

Спочатку запишемо рівняння з кутовими коефіцієнтами для наданих прямих
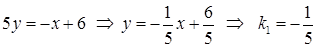
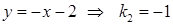 .
.
Тепер підставимо значення знайдених кутових коефіцієнтів в (2.3) для визначення кута
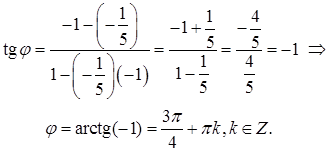
Відповідь:кут між прямими становить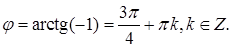
Завдання до практичного заняття № 2.
Завдання № 1.
Указати, які із прямих паралельні й перпендикулярні.
1.1 
1.2 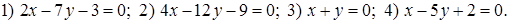
1.3 
1.4 
Завдання № 2.
Через точку М провести пряму  паралельно до прямої
паралельно до прямої  .
.
2.1 М(3,-2), 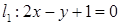 ; 2.2 М(0,-2),
; 2.2 М(0,-2),  ;
;
2.3 М(4,-1),  ; 2.4 М(3,3),
; 2.4 М(3,3),  .
.
Завдання № 3
Через точку М провести пряму  перпендикулярно до прямої
перпендикулярно до прямої  .
.
3.1 М(0,-2),  ; 3.2 М(5,-2),
; 3.2 М(5,-2),  ;
;
3.3 М(2,-1),  ; 3.4 М(4,3),
; 3.4 М(4,3),  .
.
Завдання № 4.
Знайдіть відстань від точки М до прямої.
4.1  ,
,  ; 4.2
; 4.2  ,
,  ;
;
4.3 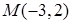 ,
, 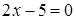 ; 4.4
; 4.4  ,
, 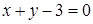 ;
;
4.5  ,
, 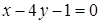 ; 4.6
; 4.6 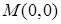 ,
, 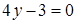 .
.
Завдання № 5.
Знайти кут між прямими.
5.1 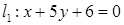 ,
,  ; 5.2
; 5.2  ,
,  .
.
5.3  ,
,  , 5.4
, 5.4  ,
, 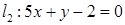 .
.
5.5 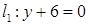 ,
, 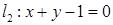 , 5.6
, 5.6  ,
,  .
.
Типові завдання(з коментарем).
Приклад 1. Знайти рівняння прямих, паралельних прямій

і віддалених від неї на відстань  .
.
Розв'язок.Для всякої точки М (х, у) шуканої прямої відповідно до формули (2.10) повинна виконуватися рівність

Звідси або 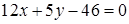 , або
, або  .
.
Відповідь: рівняння прямих 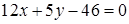 ,
,  .
.
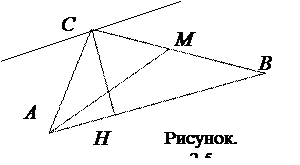 Приклад 2. Надано вершини трикутника АВС (Рисунок 2.5): А(1,–4), В(2, 2), С(5,0).
Приклад 2. Надано вершини трикутника АВС (Рисунок 2.5): А(1,–4), В(2, 2), С(5,0).
Знайти:
а) рівняння сторони АВ- пряма  ;
;
б) рівняння висоти СН- пряма  ;
;
в) рівняння медіани АМ- пряма  ;
;
г) рівняння прямої, що проходить через вершину С паралельно прямої
АВ- пряма  ;
;
д) відстань від точки С до точки Н.
Розв'язок. Знайдемо рівняння сторони АВ- прямої  .
.
Скористаємося рівнянням прямої, що проходить через дві точки (2.9)
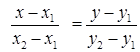 .
.
Будемо вважати точку А -першою, точку В -другою. Одержимо
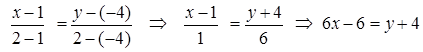 .
.

Знайдемо рівняння висоти СН- прямої  .
.
Рівняння прямої  будемо шукати у вигляді
будемо шукати у вигляді  . Пряма
. Пряма  перпендикулярна прямій
перпендикулярна прямій  , значить з (2.4):
, значить з (2.4):  Для знаходження
Для знаходження  використаємо координати точки С, що лежить на шуканій прямій і, отже, задовольняє рівнянню прямої
використаємо координати точки С, що лежить на шуканій прямій і, отже, задовольняє рівнянню прямої  . Підставимо в нього координати точки С:
. Підставимо в нього координати точки С:
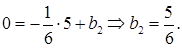
З урахуванням  одержимо рівняння прямої
одержимо рівняння прямої  з кутовим коефіцієнтом
з кутовим коефіцієнтом
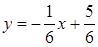
або загальне рівняння прямої  :
:
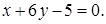
Знайдемо рівняння медіани АМ- прямої  .
.
Щоб записати рівняння прямої АМ потрібно знати координати точки М.
Точка М (  )ділить сторону СВ навпіл, тобто
)ділить сторону СВ навпіл, тобто
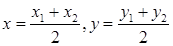 ,
,
де  .
.
Знаходимо координати точки М:
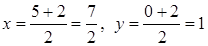 ,
,
Таким чином: М 
Скористаємося рівнянням прямої, що проходить через дві точки
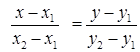 .
.
Точку А вважаємо першою, точку М – другою
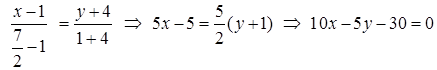 .
.
Загальне рівняння прямої АМ:

Знайдемо рівняння прямої  .
.
Рівняння прямої  будемо шукати у вигляді
будемо шукати у вигляді  . Пряма
. Пряма  паралельна прямій
паралельна прямій  , значить з (2.5):
, значить з (2.5):  Для знаходження
Для знаходження  використаємо координати точки С, що лежить на шуканій прямій і, отже, задовольняє рівнянню прямої
використаємо координати точки С, що лежить на шуканій прямій і, отже, задовольняє рівнянню прямої  . Підставимо в нього координати точки С
. Підставимо в нього координати точки С

З урахуванням  одержимо рівняння прямої
одержимо рівняння прямої  з кутовим коефіцієнтом
з кутовим коефіцієнтом

або загальне рівняння прямої  :
:
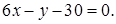
Знайдемо відстань від точки С до точки Н, тобто довжину висоти СН.
Скористаємося формулою (2.10) відстані від точки до прямої. У нашому випадку ця відстань від точки С до прямої АВ:
 .
.
Відповідь:

Заняття №3
Тема: Канонічні рівняння кривих другого порядку. Формули паралельного переносу координатних осей. Полярна система координат.
Література: [4], розділ 1, § 2, стор.27-41,
[5], розділ 1, глава 4, стор.35-52,
[5], розділ 1, глава 5, стор.52-62,
[6], глава1, § 3, стор.27-36,
[6], глава 1, § 4, стор. 37-41,
[6], глава 1, § 5, стор. 45-50.
Ціль: навчитися застосовувати формули паралельного переносу осей та приводити криві другого порядку до каноніч-ного вигляду, використовуючи формули паралельного переносу осей; вміти здійснювати перехід із декартової в полярну системи координат й навпаки.
План.
1. Коло, еліпс, гіпербола, парабола. Формула паралельного переносу осей.
2. Формули зв'язку полярної й декартової систем координат.