 |
|
Лекция 9. Спектральные свойства линейных операторов.
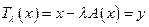
Здесь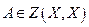 
, 
- комплексное.
Уравнение принято рассматривать в теории. Рассмотрим .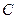 
разбивается на 2 подмножества:
1) 
- неособенные значения оператора (уравнение имеет единственное решение при любой правой части)
2) 
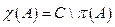- характеристическое множество.
Определение. 
называется характеристическим значением 
, если уравнение
имеет отличные от нуля решения.
Обозначим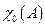 
-множество всех характеристических значений. Очевидно 
.
Определение. Каждое решение называется собственным элементом (вектором), отвечающим данному характеристическому значению .
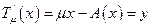
банахово 
- комплексные параметры интегральных уравнений.
Рассмотрим
1) 
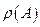- регулярные значения оператора (резольвентное множество)
2) 
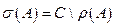- спектр.
Аналогично рассмотрим
Аналогично определяются собственные значения (числа), собственные элементы (векторы), корневое подпространство, кратность и ранг собственных значений.
Определение.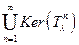 
называется корневым подпространство, а его размерность (конечная или бесконечная) – кратностью характеристического значения .
Определение. Числа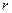 
различных множеств 
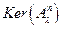называется рангом характеристического значения.
Связь между характеристическим множеством и спектром:
если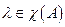 
, то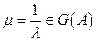 
и наоборот.
Аналогично связаны характеристические значения и собственные значения.
Простейшие свойства.
1) Соотношение 
равносильно существованию ограниченного обратного
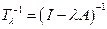
2) Множество неособенных значений открыто, а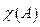 
замкнуто.
Это следует из соотношения 
и из обобщенной теоремы Банаха.
3) Круг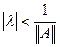 
содержится в , а спектр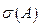 
целиком входит в круг 
.
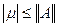Теорема. Если компактный оператор, то
а) Характеристическое множество содержит лишь характеристические значения, т.е.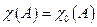 
(альтернатива Фредгольма)
б) Каждое характеристическое значение имеет конечную кратность.
в) Для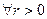 
круг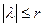 
содержит лишь конечное число характеристических значений. (сформулировать теорему в терминах собственных значений).