Главная | Обратная связь

Капитальных вложений

 

Валовые капитальные вложения (инвестиции) идут на поддержание и развитие основных производственных фондов (ОПФ) 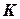. Это способствует увеличению выпуска валового продукта , т.к. одним из основных аргументов производственной функции является ОПФ 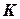. Следовательно, от того, как будут распределяться валовые капитальные вложения , будет зависеть увеличение валового продукта со всеми вытекающими из этого последствиями, в частности, объема производственного потребления , конечного продукта , непроизводственного потребления и самих валовых капитальных вложений .

Рассмотрим задачу распределения валовых капитальных вложений как статическую задачу, т.е. без учета времени, необходимого для освоения выделяемых инвестиций , а следовательно, и необходимого для увеличения .

Сформулируем эту задачу следующим образом.

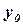Для реконструкции заводов выделено капиталовложений. Если -ому заводу выделяется капиталовложений, то на нем увеличивается выпуск продукции до величины . Требуется найти вариант распределения капиталовложений, при котором суммарное увеличение выпуска продукции всеми заводами максимально.

Обозначим:

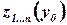- суммарное увеличение выпуска продукции всеми заводами при распределении между ними 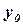капиталовложений,

- распределение по заводам капиталовложений.

Тогда задачу можно представить в виде задачи математического программирования:

при ограничениях

,

, .

При любом представлении функций , , решение этой задачи сопряжено со значительными трудностями. Поэтому представим ее моделью динамического программирования.

Методы динамического программированияприменяются для повышения эффективности вычислений при решении задач математического программирования путем их разложения (декомпозиции) на менее сложные подзадачи. Как правило, решение общей задачи математического программирования представляется последовательностью его этапов. Каждому такому этапу ставится в соответствие частная подзадача. Решение частной подзадачи осуществляется с учетом рекуррентного соотношения, отражающего принцип оптимальности Беллмана: каковы бы ни были предыдущее состояние и принятое предыдущее решение, последующие решения должны составлять оптимальную стратегию относительно состояния, возникшего в результате предыдущего решения. Это позволяет совокупность оптимальных решений частных подзадач представить как оптимальное решение общей задачи (Приложение 2).

Построим рекуррентное соотношение для рассматриваемой задачи.

Этап 1.

Если количество заводов , то

.

Этап 2.

Если количество заводов 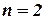, то максимальное увеличение выпуска продукции всеми ими соответствует максимальному варианту суммарного увеличения выпуска продукции вторым заводом и остальными заводами (первым заводом) при различном распределении 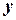капиталовложений:

.

Этап .

Продолжая аналогичные рассуждения, получим общее рекуррентное соотношение:

.

Полученное рекуррентное соотношение называется уравнением Беллманаи позволяет заменить исходную задачу на максимум функции переменных задачей на условный максимум функции одной переменной на этапах.

В рассматриваемой выше задаче распределения капиталовложений оптимальная стратегия представляет собой последовательность оптимальных значений , . .... , которая определяет оптимальное решение .

Поэтому сначала (прямой прогон) отыскивают последовательно функции Беллмана , , …, , 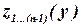как функции различных параметров 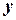соответственно.

Затем (обратный прогон) определяется оптимальное значение и соответствующее ему оптимальное значение 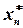. Затем оптимальное значение и соответствующее ему оптимальное значение . Продолжая этот процесс, получим оптимальные значения , ... , 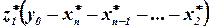и соответствующие им оптимальные значения 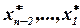, т.е. оптимальный план.