 |
|
Метод множителей Лагранжа
Рассматривая задачи условной оптимизации, пришли к выводу, что их оптимальные решения могут отличаться от экстремальных решений, найденных при поиске экстремума целевой функции без учета ограничений. Поэтому требуется свести задачу условной оптимизации к такой задаче безусловной оптимизации, т.е. к задаче без ограничений, чтобы оптимальные решения этих задач совпадали, или, другими словами, чтобы экстремальное решение задачи безусловной оптимизации совпадало с оптимальным решением задачи условной оптимизации. Тогда для поиска оптимального решения задачи условной оптимизации можно будет воспользоваться необходимым условием экстремума целевой функции соответствующей задачи безусловной оптимизации.
Сведение задачи условной оптимизации к эквивалентной, т.е. с совпадающим решением, задаче безусловной оптимизации осуществляется методом множителей Лагранжа, суть которого сводится к следующему.
Вернемся к общему виду задачи условной оптимизации:

при ограничениях
 ,
,  ;
;
 .
.
Введем вектор  множителей Лагранжа и составим из целевой функции
множителей Лагранжа и составим из целевой функции  и функций ограничений
и функций ограничений  ,
,  , функцию Лагранжа:
, функцию Лагранжа:
 .
.
Таким приемом исходная задача на условный экстремум функции  сводится к задаче на безусловный экстремум функции
сводится к задаче на безусловный экстремум функции 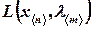 .
.
Тогда необходимыми условиямиэкстремума служат:
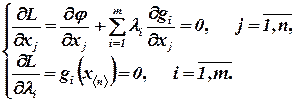
Таким образом, образуется система  алгебраических уравнений с
алгебраических уравнений с  переменными.
переменными.
Решение этой системы уравнений позволяет найти экстремальную точку функции Лагранжа, которая соответствует оптимальному решению исходной задачи условной оптимизации. Последнее определяется теоремой Куна-Таккера. Ее смысл сводится к следующему. Точка 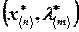 является седловой точкой функции
является седловой точкой функции  , если для всех
, если для всех  и
и  выполняется условие:
выполняется условие:
 , т.е. в седловой точке функцией
, т.е. в седловой точке функцией  достигается одновременно минимум по
достигается одновременно минимум по  и максимум по
и максимум по  .
.
Вопросы для самопроверки
Как называется универсальный метод решения задач линейного программирования и в чем его суть?
Что позволяет выявление недефицитных ограничений в задаче об использовании ресурсов?
К чему приводят изменения исходных данных статической задачи планирования производства?
Что определяют коэффициенты прямых материальных производственных затрат?
Что показывают коэффициенты полных материальных затрат?
Как из матрицы коэффициентов прямых материальных производственных затрат можно получить матрицу коэффициентов полных материальных затрат и наоборот?
Когда для решения задач математического программирования применяется метод динамического программирования?
Чем отличаются задачи условной оптимизации от задач безусловной оптимизации?
Что отражает целевая функция в задаче об использовании ресурсов (оптимального планирования производства)?
Что отражает целевая функция в задаче оптимального распределения валовых капитальных вложений?
Что представляет собой оптимальное решение задачи условной оптимизации и экстремальное решение задачи безусловной оптимизации?
Что определяют ограничения задачи условной оптимизации?
Каким методом можно свести задачу условной оптимизации к такой задаче безусловной оптимизации, чтобы оптимальные решения этих задач совпадали?
Примерырешениязадач
1.Найти экстремум функции

 .
.
Решение.
Необходимые условия экстремума:
 ,
,
 .
.
Из системы уравнений

находим  .
.
Достаточные условия экстремума:
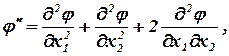
 ,
,
 .
.
Следовательно, в точке 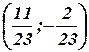 функция имеет минимум:
функция имеет минимум:
 .
.
2.Для изготовления 2-х видов продукции используются 3 типа ресурсов.
Запасы ресурсов и их расход на изготовление продукции, а также прибыль, получаемая от реализации одной единицы продукции, приведены в таблице:
| Тип ресурса | Запас ресурса | Число единиц ресурсов, затрачиваемых на изготовление одной единицы продукции | |
| 1-й вид продукции | 2-й вид продукции | ||
| 1-й тип | 0,04 | ||
| 2-й тип | 0,5 | ||
| 3-й тип | |||
| Прибыль от реализации единицы продукции |
Требуется построить математическую модель задачи линейного программирования для составления такого плана производства продукции, при котором прибыль от ее реализации будет максимальной.
Решение.

3. По данным отчетного периода получен следующий баланс трехотраслевой экономической системы:
| № отраслей | Потребители | Конечная продукция | Валовая продукция | |||
Определить валовый выпуск отраслей, обеспечивающий новый конечный продукт  .
.
Решение.
Расчет коэффициентов прямых затрат:  ,
,

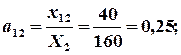

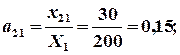







Расчет коэффициентов полных затрат:
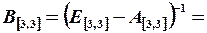 [O1]
[O1]


 [1]
[1]
Определение валового выпуска отраслей:



4.Для реконструкции трех заводов выделено 5 млн. руб. капиталовложений. Увеличение выпуска продукции (в млн. руб.) после реконструкции в зависимости от выделенного  -ому заводу
-ому заводу  объема капиталовложений
объема капиталовложений  обозначим
обозначим  и зададим в таблице:
и зададим в таблице:

| 
| 
| 
|
Необходимо найти вариант распределения капиталовложений, при котором суммарное увеличение выпуска продукции на трех заводах максимально.
Решение.
Сначала (прямой прогон) рассчитаем функции, показывающие суммарное увеличение выпуска продукции на  заводах, по рекуррентному соотношению:
заводах, по рекуррентному соотношению:
 .
.
Для  , т.е. при выделении объема капиталовложений
, т.е. при выделении объема капиталовложений 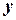 одному заводу (например, первому) функция совпадает с
одному заводу (например, первому) функция совпадает с  .
.
Рассчитаем функцию  :
:





Рассчитаем функцию 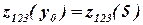 , т.к. только при полном выделении капиталовложений всем заводам достигается максимальное суммарное увеличение выпуска ими продукции:
, т.к. только при полном выделении капиталовложений всем заводам достигается максимальное суммарное увеличение выпуска ими продукции:

Затем (обратный прогон) находим, что максимальное суммарное увеличение выпуска продукции не трех заводах 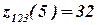 млн. руб. При этом третьему заводу выделяется 2 млн. руб. капиталовложений, а остальным двум – 3 млн. руб.
млн. руб. При этом третьему заводу выделяется 2 млн. руб. капиталовложений, а остальным двум – 3 млн. руб.
При выделении двум оставшимся заводам 3 млн. руб. капиталовложений максимальное суммарное увеличение выпуска продукции на них  млн. руб. При этом второму заводу выделяется 1 млн. руб. Тогда первому заводу выделяется оставшиеся 2 млн. руб. капиталовложений.
млн. руб. При этом второму заводу выделяется 1 млн. руб. Тогда первому заводу выделяется оставшиеся 2 млн. руб. капиталовложений.
Итак, максимальное суммарное увеличение выпуска продукции на трех заводах 32 млн. руб. при оптимальном распределении капиталовложений 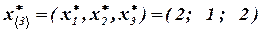 млн. руб.
млн. руб.
5.Найти условный экстремум функции

при условии (ограничении)
 .
.
Решение.
Составим функцию Лангранжа:
 .
.
Необходимые условия экстремума:
 ,
,
 ,
,
 .
.
Из системы уравнений

находим
 .
.
Достаточные условия экстремума:

Следовательно, в точке  целевая функция
целевая функция  имеет максимум:
имеет максимум:
