 |
|
Задачи условной оптимизации
Задачи условной оптимизации состоят из целевой функции и ограничений. В общем виде они представляются следующим образом:

при ограничениях
 ,
,  ;
;
 .
.
Целевая функция отражает цель оптимизации. Максимальное (минимальное) ее численное значение соответствует наилучшему варианту, определяемому значениями ее аргументов  .
.
Оптимальное решение рассматриваемой задачи - это оптимальные значения этих аргументов (обозначается  ), при которых целевая функция принимает экстремальное значение (максимальное или минимальное) и для которых выполняются все ограничения задачи.
), при которых целевая функция принимает экстремальное значение (максимальное или минимальное) и для которых выполняются все ограничения задачи.
Другими словами, ограничения задачи условной оптимизации определяют область допустимых решений этой задачи, а с помощью целевой функции среди этих допустимых решений выбирается оптимальное решение.
Заметим, что аргументы целевой функции и аргументы ограничений должны совпадать.
Задачи условной оптимизации называют задачами математического программирования. Их можно классифицировать по различным признакам.
По признаку зависимостей, описывающих целевую функцию и ограничения, эти задачи делятся на задачи линейного и нелинейного программирования.
По признаку искомых аргументов различают непрерывные и дискретные задачи.
По признаку исходных данных делят задачи на детерминированные, стохастические (случайные) и неопределенные.
Приведем примеры целевых функций, отражающих цель оптимизации. Для этого введем следующие обозначения:
 - прибыль от реализации единицы изделия
- прибыль от реализации единицы изделия 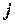 - ого вида;
- ого вида;
 - количество выпущенных изделий
- количество выпущенных изделий 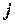 - ого вида;
- ого вида;
 - цена единицы изделия
- цена единицы изделия 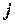 -ого вида;
-ого вида;
 - себестоимость производства единицы изделия
- себестоимость производства единицы изделия 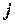 -ого вида.
-ого вида.
Используя эти обозначения, сформулируем целевые функции известных задач.
Задача рентабельности затрат на производство изделий:
 .
.
Задача рентабельности продаж:
 .
.
Задача определения затрат в расчете на рубль товарной продукции:
 .
.