Главная | Обратная связь

Учет начальных условий. Траектория выхода на магистраль

 

Если заданное начальное условие фондовооруженности предприятия совпадает с начальным значением уравнения магистрали то есть , тогда полученное уравнение магистрали (П.3.12) есть уравнение оптимального развития экономической модели предприятия.

Однако часто условие не выполняется, обычно то есть начальное условие фондовооруженности не лежит на магистрали, а находится ниже точки

В этом случае для выхода на магистраль (П.3.12), на которой обеспечивается максимум интегрального среднедушевого непроизводственного потребления, приходится сначала ограничивать среднедушевое потребление необходимым минимумом , чтобы увеличить инвестиции, нарастить фондовооруженность и выйти на магистраль.

 

Рис. П.4.1. Траектория выхода на магистраль

На рис. П.4.1 эта траектория выхода на магистраль показана зависимостью g на участке времени t = 0 ¸ t₁, где t₁ – время выхода на магистраль, после которого следует установить u = u_on. На участке выхода на магистраль t = 0 ¸ t₁ управление u = u₁ < u_on

Функция g является решением дифференциального уравнения нормированной однопродуктовой модели предприятия при фиксированном значении управления u₁

и соответствующим заданным краевым условием .

Перепишем это уравнение в виде:

где

Введем новую переменную где - коэффициент эластичности по труду.

Тогда откуда

Подставим это выражение в исходное уравнение и получим:

.

Разделив левую и правую части на получим:

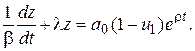
Это неоднородное линейное дифференциальное уравнение первого порядка. Общее решение его равно сумме

где - общее решение однородного дифференциального уравнения (при нулевой правой части) вида

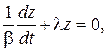
где - частотное решение неоднородного дифференциального уравнения.

Общее решение однородного дифференциального уравнения имеет вид:

,

где - константа, подлежащая определению,

- корень характеристического уравнения откуда

Тогда

Частотное решение имеет вид:

где B – коэффициент, который определим из исходного дифференциального уравнения. Для этого найдем производную и подставим ее в исходное дифференциальное уравнение, в результате получим

Разделим обе части на и определим коэффициент

Так как то , тогда уравнение траектории выхода на магистраль будет определяться из соотношения

(П.4.1)

Константу найдем из граничного условия

откуда

(П.4.2)

Время выхода на магистраль t₁ определяется из уравнения где определяется при t = t₁, а 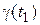- из полученного соотношения (П.4.1) при t = t₁. После подстановки получим:

 

Возведем левую и правую части в степень и получим:

Помножим левую и правую части на и получим:

откуда

 

Возьмем от левой и правой части логарифм ln и окончательно получим формулу для расчета времени выхода на магистраль t₁

, (П.4.3)

где константа определяются по выражению (П.4.2).

Если при заданном u₁ окажется, что t₁ < T , то задача выхода на магистраль может быть решена. В противном случае при t₁ > T выход на магистраль за отведенное время управления T невозможен. В этом случае нужно либо уменьшить величину u₁, либо отказаться от мечты выйти на магистраль в течении времени T. Если время выхода на магистраль t₁ < T , то управление предприятием осуществляется по графику, приведенному на рис. П.4.2.

Рис. П.4.2. График управления предприятием при

выходе на магистраль и на магистрали

Приведем пример расчета управления предприятием, выпускающим продукцию на интервале времени t = 0 ¸ 21 год. Начальное состояние предприятия: начальный капитал K(0) = 204,2 (млн. руб.), среднее число работающих на предприятии за год L(0) = 109 (чел.).

Тогда фондовооруженность на нулевой год составит:

(млн. руб. на 1 чел.)

Руководство предприятия хочет обеспечить максимум следующей целевой функции где C – непроизводственное потребление за год.

Параметры нормированной производственной функции Кобба-Дугласа следующие:

Параметры, входящие в уравнение магистрали

следующие:

Подставим приведенные значения в уравнение магистрали и получим

Проверим, совпадает ли эта магистраль с начальным значением фондовооруженности предприятия k(0) = 1,868 (млн. руб. на 1 чел.). Для этого подставим в уравнение магистрали t = 0 и получим k_оп(0) = 4,306. Оказалось, что k(0) < k_оп(0), следовательно уравнение магистрали не согласуется с начальным значением фондовооруженности предприятия.

Формула для расчета оптимальной доли средств, идущих на непроизводственное потребление, имеет вид:

Подставим в нее численные значения параметров и получим:

Так как магистраль не совпадает с начальным условием по фондовооруженности, причем k(0) > k_оп(0), то доля непроизводственного потребления не может быть установлена на всем интервале управления t = 0 ¸ 21 год.

Определим время выхода на магистраль t₁ при установленной доле непроизводственного потребления по формуле

где

 

При указанных выше параметрах результат вычисления по этой формуле дает следующий результат: t₁ = 2,2477 » 2,25 года. Тогда на интервале времени t = 0 ¸ t₁ управление u = u₁ = 0,5, а на интервале времени t = 2,25 ¸ 21 год u = u_on = 0,844.