Главная | Обратная связь

Приложение 5. Постановка задачи и критерии оптимального управления в динамических системах

 

Разнообразные реальные процессы, происходящие в окружающем мире, зачастую являются управляемыми, т.е. протекают различным образом в зависимости от конкретного воздействия на них управляющей стороны. При этом естественным является стремление выбрать в некотором смысле оптимальное управляющее воздействие, т.е. наилучшее по сравнению со всеми другими возможными способами управления. Исторически задачи оптимизации встречались еще в древние века, однако интерес к ним особенно вырос в последнее время, что связано, в частности, с ограниченностью природных ресурсов, развитием техники и ростом возможностей ЭВМ, благодаря которым стали осуществимы расчет и реализация сложных законов управления.

Результаты первоначального развития теории оптимизации объединяются в рамках классического математического анализа и вариационного исчисления, основным предметом изучения которого является исследование гладких функций и функционалов, определенных во всем пространстве или на гладком многообразии. При этом необходимые условия экстремума записываются в виде условий стационарности (обращение в нуль производной или градиента функции, уравнение Эйлера и т.д.).

Однако в процессе эволюции общества возникли новые задачи управления, в которых управляющие параметры могут принадлежать некоторому замкнутому множеству.

Необходимость управлять процессом оптимально, т.е. наилучшим в определенном смысле образом, возникает в системах, характеристики которых меняются во времени под влиянием управлений. К такому классу систем относятся и экономические системы. Для того чтобы сформулировать на математическом языке задачу управления в таких системах, необходимо ввести некоторые понятия и построить соответствующую математическую модель.

Важнейшими понятиями в теории оптимального управления являются понятия состояния системы и управления. Будем рассматривать системы, состояние которых может быть в любой момент времени определено вектором m-мерного векторного пространства с координатами . Пространство X будем называть пространством состояния системы, а элементы - переменными состояния системы.

Так как система изменяется во времени, то ее поведение можно описать последовательностью состояний. Такую последовательность состояний системы называют траекторией системы.

Переменную t, которая является независимой, назовем аргументом процесса. Аргументом процесса может быть любая величина, но чаще всего – время. Переменная t может пробегать некоторый отрезок числовой прямой, если или отрезок натурального ряда t = t₀ , t₀ + 1, ¼ , T. В первом случае процесс, происходящий в системе, называется непрерывным, во втором случае – дискретным или многошаговым. Системы в этих случаях называются соответственно непрерывными и дискретными (многошаговыми).

Изменение состояния системы, т.е. процесс в ней, может происходить под воздействием управляющих воздействий. Будем рассматривать системы, управляющие воздействия в которых моделируются с помощью элементов r–мерного векторного пространства U:

.

Управляющие воздействия могут задаваться в виде функций от t. Тем самым реализуется определенный способ управления системой. В этом случае будем говорить о задании программы управления

На возможные (допустимые) состояния системы и управления 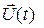могут быть наложены ограничения. Ограничения на состояние системы и управление могут быть записаны в виде

,

где - пространства с размерностями m и r соответственно.

Вектор 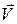, образованный парой функций , назовем процессом с допустимым пространством V размерности m+r. Между функциями 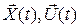имеется связь: как только задано управление системой, то последовательность ее состояний (траектория системы) определяется однозначно. Связь между и моделируется по-разному в зависимости от того, является система непрерывной или дискретной. Для непрерывных систем модели процессов описываются в пространстве состояний системой дифференциальных уравнений вида

, (П.5.1)

 

где f_i – известные (линейные или нелинейные) функции,

Систему уравнений (П.5,1) можно записать в векторной форме в виде

, (П.5.2)

или в виде

.

 

Пусть задано состояние, в котором система находилась в начальный момент t₀ . Этот момент в дальнейшем для определенности примем равным нулю, а момент окончания процесса t₁ равным T. Тогда аргумент процесса t изменяется в пределах 0 £ t £ T, а начальным состоянием системы будет вектор

,

где x_i(0) – начальное значение i–той координаты вектора состояния системы.

Проанализируем, каким образом модель отражает связь между управлением и состоянием системы, изменяющимся под воздействием управления. Пусть на промежутке 0 £ t £ T задано управление . Подставляя его в правую часть системы (2), получим

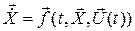(П.5.3)

Имеем систему дифференциальных уравнений относительно неизвестной вектор - функции . Решая ее с учетом начальных условий 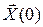, получим . Это решение и есть траектория, отвечающая заданному управлению . При этом мы предполагаем, что для системы (П.5.3) выполнены условия, обеспечивающие существование и единственность ее решения при заданных начальных условиях (решение задачи Коши).

Итак, задание управления в непрерывной модели однозначно определяет ее поведение. Задавая различные законы управления, получаем, следовательно, различные траектории системы.

Модель дискретной управляемой системы имеет вид системы разностных уравнений:

 

В векторной форме эту модель, как и в непрерывном случае, будем записывать в виде

,

или в виде

(П.5.4)

Здесь t – номер цикла принимает дискретные значения t = 0, 1, 2, ¼, T - 1. Начальное значение 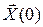будем, как и выше, считать известным.

В дискретной системе, как и в непрерывной, задание программы управления при t = 0, 1, 2, ¼, T – 1 позволяет однозначно определить соответствующую ей траекторию системы. При этом в дискретном случае не требуется наложения каких-либо условий на правые части уравнений (П.5.4), как в непрерывном случае, где требовалось обеспечить существование и единственность задачи Коши. В самом деле, при подстановке значения в правую часть (П.5.4) получаем систему уравнений, которая позволяет при известном значении состояния в момент времени t определить состояние 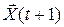в следующий момент времени. Так как в начальный момент t = 0 состояние 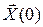известно, то, подставив его в правую часть (4), получим

.

Подставляя затем найденное значение и t = 1 в (4), так же найдем значение . Продолжая этот процесс, через T шагов получим последнее искомое значение .

Таким образом и в дискретном случае уравнения модели (4) позволяют однозначно определить траекторию системы , если задано управление .

Следовательно, процесс должен удовлетворять следующим ограничениям:

Процессы или 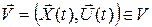при всех 0 £ t £ T.

Пара удовлетворяет системе уравнений (П.5.2) в непрерывной модели при или (П.5.4) в дискретной модели при t = 0, 1, ¼, T – 1.

Заданы начальные условия .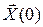

В непрерывной модели на вектор-функции 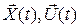накладываются некоторые дополнительные ограничения: вектор–функцию будем считать кусочно-непрерывной, а вектор-функцию - непрерывной и кусочно-дифференцируемой.

Процессы , удовлетворяющие указанным условиям, будем называть допустимыми. Таким образом, допустимый процесс - это программа управления и соответствующая ей траектория системы , удовлетворяющие перечисленным ограничениям.

Множество допустимых процессов в задачах оптимального управления представляет собой множество M допустимых элементов. Теперь для постановки оптимизационной задачи необходимо ввести в рассмотрение целевую функцию или функционал J, заданный на множестве M. Задача оптимального управления будет состоять в выборе такого элемента множества M, на котором функционал J достигает экстремального значения. Такой процесс мы будем называть оптимальным процессом, управление 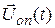- оптимальным управлением, а траекторию - оптимальной траекторией.

Функционал J, заданный на множестве допустимых процессов, описывает цель, согласно которой оптимизируется процесс, поэтому его часто называют целевой функцией.

Значение J(V₀), которое функционал J принимает на данном процессе V₀, характеризует качество процесса и позволяет сравнить два любых процесса. Оптимальным, т.е. более предпочтительным по сравнению с любым другим процессом, будет тот, где значение функционала минимально (максимально).

В задачах оптимального управления для непрерывных систем чаще всего применяются интегральные функционалы следующего вида:

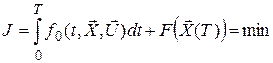, (П.5.5)

где - заданные подынтегральная и терминальная функции. Выражение (П.5.5) позволяет вычислить для каждого допустимого процесса определенное значение J и тем самым задать функционал на множестве допустимых процессов. Для этого необходимо подставить вместо аргументов функции , которая становится функцией времени, после чего вычислить интеграл. Затем к значению интеграла прибавляем значение терминальной функции при .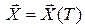

Функционал J состоит из двух частей: значения интеграла и функции конечного состояния 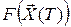- терминальной функции. Первое из этих слагаемых оценивает качество процесса на на всем промежутке [0, T], второе слагаемое – качество конечного состояния системы. Иногда в задачах оптимального управления конечное состояние системы задается. В этом случае второе слагаемое функционала (П.5.5) есть величина постоянная и, следовательно, не влияет на его минимизацию. Такие задачи называются задачами с фиксированным правым концом траектории. Условие 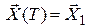следует добавить в качестве дополнительного ограничения к условиям, определяющим множество допустимых процессов. Функционал (П.5.5) выбирается таким образом, чтобы содержательный смысл входящих в него слагаемых отвечал цели управления в конкретной задаче.

В частных случаях любое из слагаемых в (П.5.5) может отсутствовать. Тогда функционал будет иметь вид

, (П.5.6)

или

. (П.5.7)

Возникающие в этих случаях оптимизационные задачи могут быть сведены одна к другой и, следовательно, ни одна из них не является более общей.

В литературе по оптимальному управлению оптимизационные задачи с функционалом вида (П.5.5) называют задачами Больца, с функционалом вида (П.5.6) - задачами Лагранжа, а с функционалом вида (П.5.7) - задачами Майера.

Покажем, что задача Больца может быть сведена к задаче Майера. Для этого введем еще одну скалярную переменную состояния x_m+1(t), определяемую соотношениями

.

Тогда

.

 

Поэтому функционал (П.5.5) можно записать следующим образом в виде (П.5.7)

,

что соответствует задаче Майера.

Аналогично в случае дифференцируемости по времени функции 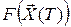задача Майера может быть сведена к задаче Лагранжа.

Отметим, что если в задаче Лагранжа (П.5.6) подынтегральная функция равна единице, т.е. , то функция .

Такая задача, заключающаяся в минимизации времени управления T, называется задачей на быстродействие.

Функционалы вида (П.5.5) охватывают широкий класс задач оптимального управления, в том числе и оптимизации экономических процессов.

Для задач оптимизации в дискретных системах функционал имеет вид

. (П.5.8)

 

К функционалу (П.5.8) относятся все замечания и комментарии, сделанные к функционалу (П.5.5).

Итак, мы определили все понятия, необходимые для постановки задач оптимального управления. Поставим задачу о минимуме функционала (П.5.5) в непрерывном и (П.5.8) в дискретном случае на множестве M допустимых процессов . Она может быть сформирована в двух вариантах:

Определить оптимальный процесс для непрерывной системы , чтобы J = min.

Определить минимизирующую последовательность для дискретной системы , чтобы J = min.

Задача оптимального управления, как правило, ставится в первом варианте. Но тогда она, как мы убедились, не всегда имеет решение. В то же время во втором варианте задача оптимального управления всегда имеет решение, если только функционал J ограничен снизу на множестве M. Последнее условие часто удается проверить достаточно просто. Например, в большом количестве экономических приложений функции являются неотрицательными при любом наборе аргументов. В этом случае функционал J не может принимать отрицательных значений. Следовательно, он ограничен снизу.

В теории оптимального управления термины «состояние» и «управление» имеют наглядный содержательный смысл. Он заключается в том, что, как отмечалось выше, задавая управление , мы задаем и траекторию процесса , а изменяя программу - управляем процессом. Здесь t = 0, 1, 2, ¼ - номера циклов.

Кроме того, имеются и некоторые формальные отличия: в непрерывном варианте состояние входит в уравнение процесса вместе со своей производной , а управление - непосредственно. Это обуславливает различные математические требования к классам функций, к которым принадлежат функции . В дискретном случае состояние входит в отличие от управления в управление процессом вместе со своим значением 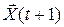в момент времени (t + 1).

Приведем примеры, иллюстрирующие постановку задач оптимального управления.

Пример 1. Рассмотрим открытую модель Леонтьева, которая описывается следующим балансовым соотношением:

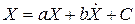(П.5.9)

Соотношение (П.5.9) показывает, как валовая продукция X распределяется на производственные затраты aX, прирост основных производственных фондов и потребление С.

Если рассматривать развитие экономики на некотором промежутке времени , то различные альтернативы ее развития определяются тем, как задается потребление C. Задав его на промежутке [0, T], найдем однозначно из уравнения модели траекторию роста валового продукта X(t).

Чтобы пояснить последнее, представим уравнение (П.5.9) в виде

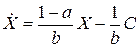(П.5.10)

 

Из (П.5.10) видно, что при задании C(t) это соотношение превращается в дифференциальное уравнение относительно X(t) с заданной правой частью, откуда величина X(t) может быть найдена. Кроме того, известны начальное состояние X(0) и ограничения на минимальную и максимальную величину потребления. Если учесть и вытекающую из экономического смысла неотрицательность переменных в рассматриваемой модели, то перечисленные ограничения можно представить в виде

X(0) = X₀ , C_min £ C £ C_max , X ³ 0. (П.5.11)

Если теперь воспользоваться терминологией, введенной ранее для постановки задач управления, то соотношение (П.5.10) представляет собой уравнение процесса, C – управление, X – состояние системы. Накладываемые на процесс ограничения определяются соотношениями (П.5.11).

Таким образом, соотношения (П.5.10), (П.5.11) определяют множество допустимых в данной системе процессов.

Чтобы определить наиболее эффективный путь экономического роста, т.е. выбрать из множества допустимых процессов наилучший, требуется задать функционал J, определяющий качество процесса. Отметим, что выбор критерия оптимальности развития экономической системы – самостоятельная, имеющая важное значение, проблема экономики.

Критерий, предусматривающий рост потребления и возможность наращивать определенный экономический потенциал к конечному моменту времени, может быть выражен функционалом следующего вида:

. (П.5.12)

 

Здесь первое слагаемое представляет собой суммарное взвешенное потребление на промежутке [0,T], терминальный член имеет смысл объема выпуска продукции в конечный момент времени. Весовые коэффициенты a, b говорят о приоритете, который имеет каждое из этих слагаемых. Если мы отдаем предпочтение потреблению, то a ³ b , а если предпочтение отдается накоплению производственного потенциала, то a < b. Подынтегральное выражение - дисконтированное потребление, - взвешивающая функция, d - коэффициент дисконтирования.

Итак, рассмотренная динамическая модель распределения валового продукта с учетом цели развития экономического объекта является задачей оптимального управления с функционалом J, заданным соотношением (П.5.12) и ограничениями (П.5.10), (П.5.11), которым должен удовлетворять допустимый процесс. Эта задача полностью соответствует сформулированной выше задаче оптимального управления. Отметим, что речь идет о максимизации функционала J, что эквивалентно минимизации функционала -J, т.е. функционала, взятого с противоположным знаком.

Пример 2. Рассмотрим задачу оптимального распределения капитальных вложений в отрасли на заданном интервале планирования.

Обозначим через K(t) величину основных производственных фондов отрасли в году t. В процессе воспроизводства основных производственных фондов их количество будет расти за счет капитальных вложений, а уменьшаться за счет физического и морального износа.

Будем считать, что ввод в действие основных фондов в году t, численно равный I(t), удовлетворяет ограничениям

, (П.5.13)

где минимальное и максимальное значения ввода в действие основных фондов – известные постоянные или зависящие от времени функции, а величина выбытия фондов в году t равна . Тогда уравнение баланса основных фондов, отражающее равенство прироста основных производственных фондов в году t за счет ввода их в действие и за счет выбытия примет вид

(П.5.14)

или

(П.5.15)

где - прирост основных фондов в году.

Уравнение (П.5.15) является дискретной моделью роста основных фондов отрасли.

Будем считать заданным начальное значение основных фондов. Учитывая естественное условие их неотрицательности, имеем

. (П.5.16)

Теперь можно рассматривать в качестве характеристики происходящего в системе процесса пару , считая K(t) состоянием системы, I(t) - управлением, а (П.5.15) – уравнением процесса. Тогда множество M допустимых процессов задается условиями (П.5.13), (П.5.15), (П.5.16).

Качество протекающего в системе процесса изменения основных фондов зададим функционалом

, (П.5.17)

 

где a, b - некоторые неотрицательные числа.

Выражение (П.5.17), являющееся критерием оптимальности процессов, состоит из двух слагаемых. Для того чтобы пояснить экономический смысл критерия, положим a = 1, b = 0. Тогда , и минимизация этого функционала отражает требование максимальной экономии капиталовложений. Если же a = 0, b = 1, то J = - K(T), и минимизация такого функционала равносильна максимизации K(t) значения основных фондов в конце планового периода.

Таким образом в функционале (П.5.17) отражены два, вообще говоря, противоположных требования к процессу - экономии капиталовложений с одной стороны и увеличения основных производственных фондов отрасли – с другой. Числа a, b являются весовыми коэффициентами. Если a > b, то приоритет отдается первому требованию, если a < b, то второму.

Таким образом, имеем задачу оптимального управления дискретным процессом, заданным уравнением (П.5.15) с функционалом (П.5,17), ограничениями на управление (П.5.13) и на состояние (П.5.16).

В данной постановке задачи оптимального управления правый конец траектории K(t) является свободным, так как отсутствует ограничение на значение K(t). Вместе с тем, если положить в функционале (П.5.17) a = 1, b = 0, то при этом естественно наложить требование на значение K(t). Иначе I(t) º 0, и задача теряет экономический смысл. В рассматриваемом случае будем считать заданным K(t) = K₁, где величина K₁ задает наряду с функционалом J цель управления системой.

Пример 3. Рассмотрим непрерывный вариант модели оптимального распределения капитальных вложений. Такая модель представляет интерес для теоретических исследований. Составим уравнение баланса основных фондов отрасли в непрерывном варианте.

Величина DK прироста основных фондов на промежутке [t, t +Dt] будет равна K(t+Dt) - K(t). В отличие от введенных в дискретной модели переменных обозначим через I(t) интенсивность ввода основных фондов в момент времени t. Под интенсивностью будем понимать количество вводимых в единицу времени фондов. Тогда на рассматриваемом промежутке будет введено I(t)Dt единиц основных фондов. Обозначим через m интенсивность выбытия основных фондов. Тогда общее количество выводимых из производства за время Dt фондов будет равно mDtI(t). С учетом сказанного уравнение баланса (14) можно записать в виде

. (П.5.18)

Если разделить обе части последнего уравнения на Dt и перейти к пределу при Dt®0, слева получим значение производной, а уравнение (П.5.18) перепишем следующим образом:

. (П.5.19)

К этому нужно добавить начальное условие и ограничения на значения переменных:

. (П.5.20)

Рассматривая данный процесс как управляемый, будем, как и в примере 2, считать K(t) состоянием процесса, I(t) – управлением. Процесс описывается уравнением (П.5.19), которое вместе с ограничениями (П.5.20) определяет множество M допустимых процессов .

Обобщением функционала (П.5.17) на непрерывный случай будет функционал вида

. (П.5.21)

 

Теперь задача оптимального управления заключается в отыскании оптимального процесса , являющегося допустимым и минимизирующего функционал (П.5.21).

Как и в примере 2, если в выражении (П.5.21) b = 0, требуется задать конечное состояние K(t) = K₁.

Пример 4. Рассмотрим задачу оптимального распределения капитальных вложений между отраслями.

Этот пример является обобщением примеров 2 и 3 для нескольких отраслей. Как и выше, речь пойдет о распределении ограниченного объема вводимых в действие основных производственных фондов на некотором интервале времени . Отличие состоит в том, что распределение нужно осуществить не только во времени, но и между отраслями, которые являются в данном случае «конкурентами».

Пусть имеются отрасли с номерами i = 1, 2, ¼, n. Если в i – ой отраcли K_i(t) – основные производственные фонды в году t, m_i - коэффициент ежегодного выбытия фондов (коэффициент амортизации), I_i(t) - объем вводимых в действие в году t основных фондов, то для каждой из отраслей можно написать уравнение баланса основных фондов, аналогичное (П.5.15):

(П.5.22)

Известны основные фонды отраслей на начальный год t = 0:

K_i(0) i = 1, 2, ¼, n. (П.5.23)

Это будет начальным условием для системы уравнений (П.5.22).

Кроме того, суммарная величина вводимых в действие основных фондов ограничена. С учетом перечисленных ограничений на переменные модели можно записать

. (П.5.24)

 

Соотношения (П.5.22) – (П.5.24) описывают ограничения на множество допустимых процессов .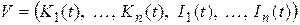

Обобщением на случай n отраслей функционала (П.5.17) будет

. (П.5.25)

 

Функционал (П.5.25) вместе с ограничениями (П.5.22) – (П.5.24) определяет задачу оптимального управления. Состоянием процесса здесь является вектор основных фондов отраслей, управлением – вектор вводимых в действие фондов.

Сформулированная задача оптимального управления относится к классу задач оптимизации дискретных процессов. Может быть также поставлена аналогичная задача и в непрерывном времени. Для этого необходимо заменить систему разностных уравнений (П.5.22) системой дифференциальных уравнений

. (П.5.26)

а функционал (П.5.25) – выражением

. (П.5.27)

 

Тогда получим непрерывную задачу оптимального управления, описываемую функционалом (П.5.27), уравнениями процесса (П.5.26) и ограничениями (П.5.23), (П.5.24).